浙江台州三梅中学2020学年第一学期高二年级第一次教学检测试题Word版无答案
文档属性
| 名称 | 浙江台州三梅中学2020学年第一学期高二年级第一次教学检测试题Word版无答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 430.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览

文档简介
三梅中学2020学年第一学期高二年级第一次教学检测试题
数学试题卷
2020.10
选择题(每题4分,10题共40分)
1.用符号表示“点A在直线l上,l在平面α内”,正确的是( )
A.A∈l,l?α
B.A?l,l?α
C.A?l,l∈α
D.A∈l,l?α
2.如图的组合体是由()组合而成.
A.两个棱柱
B.棱柱和圆柱
C.圆柱和棱台
D.圆锥和棱柱
3.
如图,△A'B'C'是水平放置的△ABC的直观图,A'B'∥y'轴,B'C'∥x'轴,A'B'=2,B'C'=3,则△ABC中,AC=( )
A.2
B.
C.4
D.
5
4.下列说法正确的是( )
A.过平面外一点作此平面的垂面是唯一的
B.过直线外一点作此直线的垂线是唯一的
C.过平面的一条斜线作此平面的垂面是唯一的
D.过直线外一点作此直线的平行平面是唯一的
5.已知m,n表示两条不同的直线,α表示平面.下列说法正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,m⊥n,则n∥α
C.若m⊥α,n?α,则m⊥n
D.若m∥α,m⊥n,则n⊥α
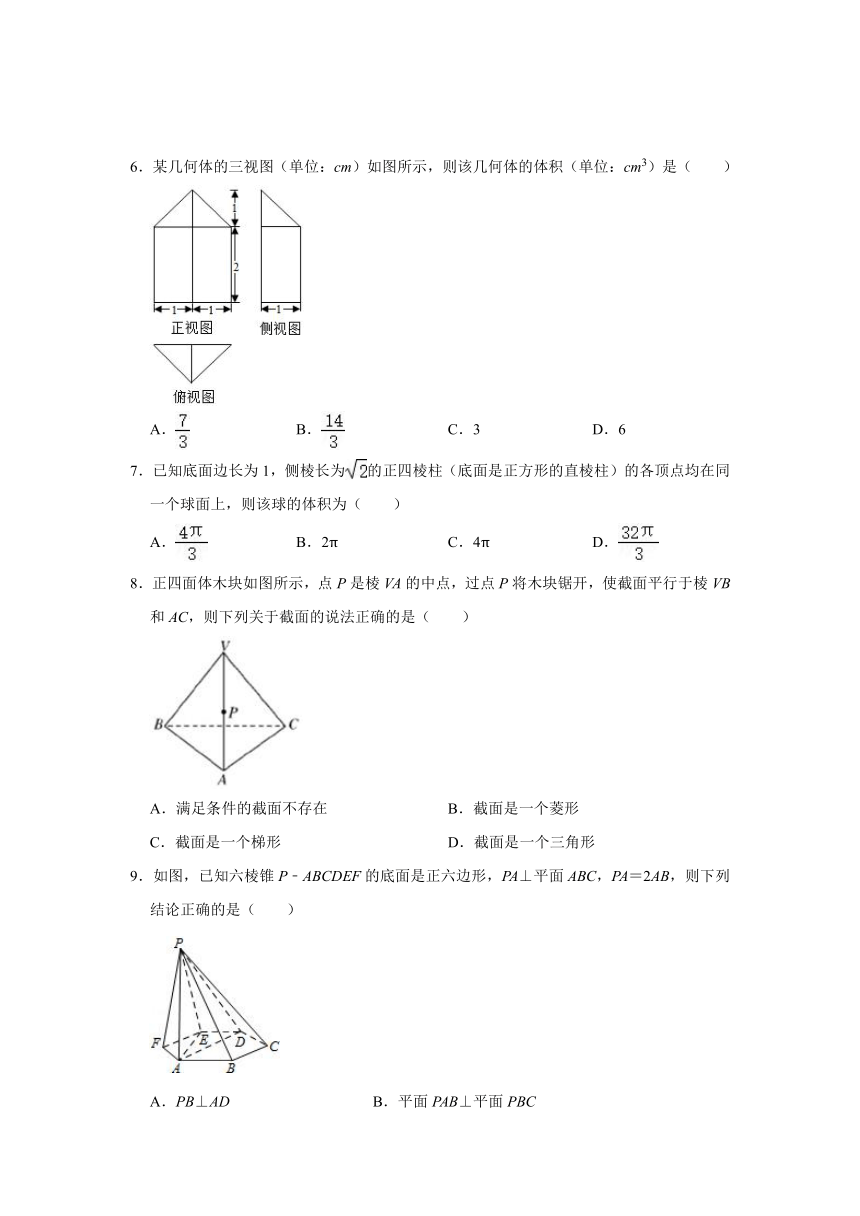
6.某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是( )
A.
B.
C.3
D.6
7.已知底面边长为1,侧棱长为的正四棱柱(底面是正方形的直棱柱)的各顶点均在同一个球面上,则该球的体积为( )
A.
B.2π
C.4π
D.
8.正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,则下列关于截面的说法正确的是( )
A.满足条件的截面不存在
B.截面是一个菱形
C.截面是一个梯形
D.截面是一个三角形
9.如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是( )
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
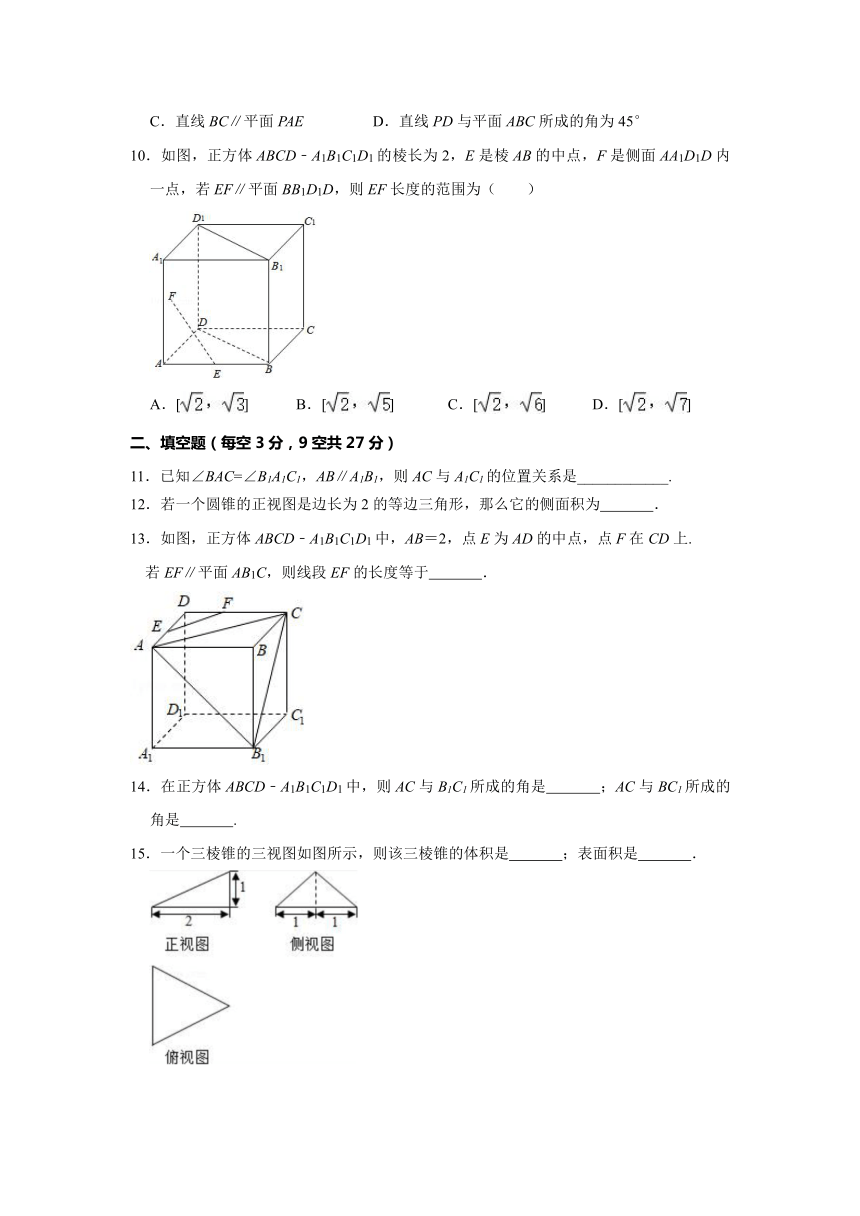
10.如图,正方体ABCD﹣A1B1C1D1的棱长为2,E是棱AB的中点,F是侧面AA1D1D内一点,若EF∥平面BB1D1D,则EF长度的范围为( )
A.[]
B.[]
C.[]
D.[]
填空题(每空3分,9空共27分)
11.已知∠BAC=∠B1A1C1,AB∥A1B1,则AC与A1C1的位置关系是____________.
12.若一个圆锥的正视图是边长为2的等边三角形,那么它的侧面积为
.
13.如图,正方体ABCD﹣A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.
若EF∥平面AB1C,则线段EF的长度等于
.
14.在正方体ABCD﹣A1B1C1D1中,则AC与B1C1所成的角是
;AC与BC1所成的角是
.
15.一个三棱锥的三视图如图所示,则该三棱锥的体积是
;表面积是
.
16.如图,二面角α﹣l﹣β的大小是60°,线段AB?α.B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是
.
17.
如图,在长方形ABCD中,AB=,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
.
解答题(5题共53分)
18.(8分)已知圆柱的底面半径长为1,母线长为2,求它的侧面积和体积.
19.(10分).如图,AB是⊙O的直径,VA垂直⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点.
(I)求证:MN∥平面ABC
(II)求证:BC⊥平面VAC
20.(11分)如图,在棱长均为1的直三棱柱ABC﹣A1B1C1中,D是BC的中点.
(I)求证:平面ADC1⊥平面BCC1B1;
(II)求直线AC1与面BCC1B1所成角的正弦值.
21.(12分)如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(I)求证:PB∥平面AEC;
(II)设异面直线BP与CD所成角为45°,AP=1,AD=,求三棱锥E﹣ACD的体积.
22.(12分)如图,在三棱台ABC﹣DEF中,平面ACFD⊥平面ABC,
∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
数学试题卷
2020.10
选择题(每题4分,10题共40分)
1.用符号表示“点A在直线l上,l在平面α内”,正确的是( )
A.A∈l,l?α
B.A?l,l?α
C.A?l,l∈α
D.A∈l,l?α
2.如图的组合体是由()组合而成.
A.两个棱柱
B.棱柱和圆柱
C.圆柱和棱台
D.圆锥和棱柱
3.
如图,△A'B'C'是水平放置的△ABC的直观图,A'B'∥y'轴,B'C'∥x'轴,A'B'=2,B'C'=3,则△ABC中,AC=( )
A.2
B.
C.4
D.
5
4.下列说法正确的是( )
A.过平面外一点作此平面的垂面是唯一的
B.过直线外一点作此直线的垂线是唯一的
C.过平面的一条斜线作此平面的垂面是唯一的
D.过直线外一点作此直线的平行平面是唯一的
5.已知m,n表示两条不同的直线,α表示平面.下列说法正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,m⊥n,则n∥α
C.若m⊥α,n?α,则m⊥n
D.若m∥α,m⊥n,则n⊥α
6.某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是( )
A.
B.
C.3
D.6
7.已知底面边长为1,侧棱长为的正四棱柱(底面是正方形的直棱柱)的各顶点均在同一个球面上,则该球的体积为( )
A.
B.2π
C.4π
D.
8.正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,则下列关于截面的说法正确的是( )
A.满足条件的截面不存在
B.截面是一个菱形
C.截面是一个梯形
D.截面是一个三角形
9.如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是( )
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
10.如图,正方体ABCD﹣A1B1C1D1的棱长为2,E是棱AB的中点,F是侧面AA1D1D内一点,若EF∥平面BB1D1D,则EF长度的范围为( )
A.[]
B.[]
C.[]
D.[]
填空题(每空3分,9空共27分)
11.已知∠BAC=∠B1A1C1,AB∥A1B1,则AC与A1C1的位置关系是____________.
12.若一个圆锥的正视图是边长为2的等边三角形,那么它的侧面积为
.
13.如图,正方体ABCD﹣A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.
若EF∥平面AB1C,则线段EF的长度等于
.
14.在正方体ABCD﹣A1B1C1D1中,则AC与B1C1所成的角是
;AC与BC1所成的角是
.
15.一个三棱锥的三视图如图所示,则该三棱锥的体积是
;表面积是
.
16.如图,二面角α﹣l﹣β的大小是60°,线段AB?α.B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是
.
17.
如图,在长方形ABCD中,AB=,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
.
解答题(5题共53分)
18.(8分)已知圆柱的底面半径长为1,母线长为2,求它的侧面积和体积.
19.(10分).如图,AB是⊙O的直径,VA垂直⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点.
(I)求证:MN∥平面ABC
(II)求证:BC⊥平面VAC
20.(11分)如图,在棱长均为1的直三棱柱ABC﹣A1B1C1中,D是BC的中点.
(I)求证:平面ADC1⊥平面BCC1B1;
(II)求直线AC1与面BCC1B1所成角的正弦值.
21.(12分)如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(I)求证:PB∥平面AEC;
(II)设异面直线BP与CD所成角为45°,AP=1,AD=,求三棱锥E﹣ACD的体积.
22.(12分)如图,在三棱台ABC﹣DEF中,平面ACFD⊥平面ABC,
∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
