初中数学暑期讲义——圆的有关性质(无答案)
文档属性
| 名称 | 初中数学暑期讲义——圆的有关性质(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 166.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-07 00:00:00 | ||
图片预览



文档简介
第六讲 圆(一)
——考点汇总
考点一、圆的相关概念
1、圆的定义
在一个个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径。
2、圆的几何表示
以点O为圆心的圆记作“⊙O”,读作“圆O”
考点二、弦、弧等与圆有关的定义
(1)弦
连接圆上任意两点的线段叫做弦。(如图中的AB)
(2)直径
经过圆心的弦叫做直径。(如途中的CD)
直径等于半径的2倍。
(3)半圆
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
(4)弧、优弧、劣弧
圆上任意两点间的部分叫做圆弧,简称弧。
弧用符号“⌒”表示,以A,B为端点的弧记作“”,读作“圆弧AB”或“弧AB”。
大于半圆的弧叫做优弧(多用三个字母表示);小于半圆的弧叫做劣弧(多用两个字母表示)
考点三、垂径定理及其推论
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
垂径定理及其推论可概括为:
过圆心
垂直于弦
直径 平分弦 知二推三
平分弦所对的优弧
平分弦所对的劣弧
考点四、圆的对称性
1、圆的轴对称性
圆是轴对称图形,经过圆心的每一条直线都是它的对称轴。
2、圆的中心对称性
圆是以圆心为对称中心的中心对称图形。
考点五、弧、弦、弦心距、圆心角之间的关系定理
1、圆心角
顶点在圆心的角叫做圆心角。
2、弦心距
从圆心到弦的距离叫做弦心距。
3、弧、弦、弦心距、圆心角之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦想等,所对的弦的弦心距相等。
推论:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
考点六、圆周角定理及其推论
1、圆周角
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
2、圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
考点七、点和圆的位置关系
设⊙O的半径是r,点P到圆心O的距离为d,则有:
dd=r点P在⊙O上;
d>r点P在⊙O外。
考点八、过三点的圆
1、过三点的圆
不在同一直线上的三个点确定一个圆。
2、三角形的外接圆
经过三角形的三个顶点的圆叫做三角形的外接圆。
3、三角形的外心
三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,它叫做这个三角形的外心。
4、圆内接四边形性质(四点共圆的判定条件)
圆内接四边形对角互补。
考点九、反证法
先假设命题中的结论不成立,然后由此经过推理,引出矛盾,判定所做的假设不正确,从而得到原命题成立,这种证明方法叫做反证法。
考点十、直线与圆的位置关系
直线和圆有三种位置关系,具体如下:
(1)相交:直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线,公共点叫做交点;
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,
(3)相离:直线和圆没有公共点时,叫做直线和圆相离。
如果⊙O的半径为r,圆心O到直线l的距离为d,那么:
直线l与⊙O相交d直线l与⊙O相切d=r;
直线l与⊙O相离d>r;
考点十一、切线的判定和性质
1、切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线。
2、切线的性质定理
圆的切线垂直于经过切点的半径。
考点十二、切线长定理
1、切线长
在经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长。
2、切线长定理
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
考点十三、三角形的内切圆
1、三角形的内切圆
与三角形的各边都相切的圆叫做三角形的内切圆。
2、三角形的内心
三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心。
考点十四、圆和圆的位置关系
1、圆和圆的位置关系
如果两个圆没有公共点,那么就说这两个圆相离,相离分为外离和内含两种。
如果两个圆只有一个公共点,那么就说这两个圆相切,相切分为外切和内切两种。
如果两个圆有两个公共点,那么就说这两个圆相交。
2、圆心距
两圆圆心的距离叫做两圆的圆心距。
3、圆和圆位置关系的性质与判定
设两圆的半径分别为R和r,圆心距为d,那么
两圆外离d>R+r
两圆外切d=R+r
两圆相交R-r两圆内切d=R-r(R>r)
两圆内含dr)
4、两圆相切、相交的重要性质
如果两圆相切,那么切点一定在连心线上,它们是轴对称图形,对称轴是两圆的连心线;相交的两个圆的连心线垂直平分两圆的公共弦。
考点十五、正多边形和圆
1、正多边形的定义
各边相等,各角也相等的多边形叫做正多边形。
2、正多边形和圆的关系
只要把一个圆分成相等的一些弧,就可以做出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆。
考点十八、弧长和扇形面积
1、弧长公式
n°的圆心角所对的弧长l的计算公式为
2、扇形面积公式
其中n是扇形的圆心角度数,R是扇形的半径,l是扇形的弧长。
3、圆锥的侧面积
其中l是圆锥的母线长,r是圆锥的地面半径。
补充:
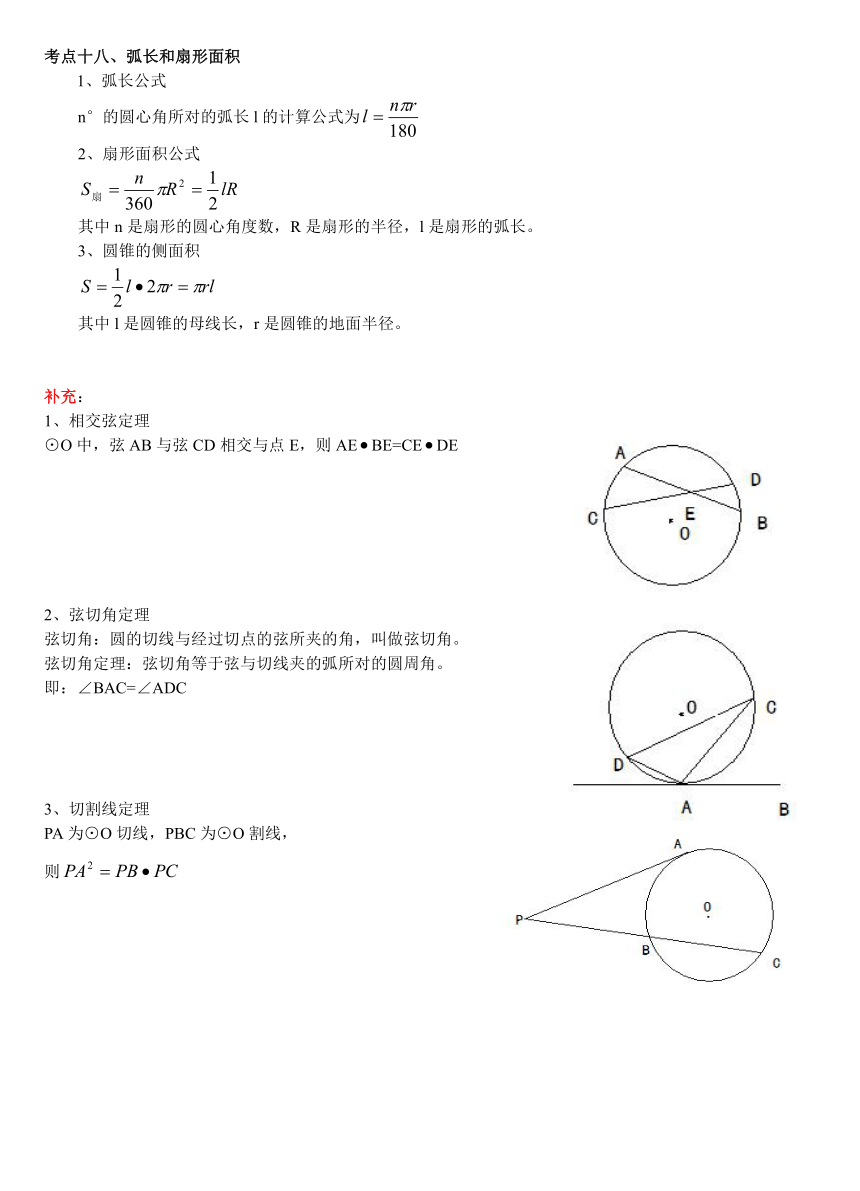
1、相交弦定理
⊙O中,弦AB与弦CD相交与点E,则AEBE=CEDE
2、弦切角定理
弦切角:圆的切线与经过切点的弦所夹的角,叫做弦切角。
弦切角定理:弦切角等于弦与切线夹的弧所对的圆周角。
即:∠BAC=∠ADC
3、切割线定理
PA为⊙O切线,PBC为⊙O割线,
则
1. (2011浙江金华,21,8分)如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE.
(1)求证:AP=AO;
(2)若tan∠OPB=,求弦AB的长;;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 ,能构成等腰梯形的四个点为 或 或 .
2. (2011山东德州22,10分)●观察计算
当,时, 与的大小关系是_________________.
当,时, 与的大小关系是_________________.
●探究证明
如图所示,为圆O的内接三角形,为直径,过C作于D,设,BD=b.
(1)分别用表示线段OC,CD ;
(2)探求OC与CD表达式之间存在的关系
(用含a,b的式子表示).
●归纳结论
根据上面的观察计算、探究证明,你能得出与的大小关系是:_________________________.
●实践应用
要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
3. (2011山东济宁,19,6分)如图,为外接圆的直径,,垂足为点,的平分线交于点,连接,.
(1) 求证:;
(2) 请判断,,三点是否在以为圆心,以为半径的圆上?并说明理由.
4. (2011山东烟台,25,12分)已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
5. (2011湖南常德,25,10分)已知 △ABC,分别以AC和BC为直径作半圆、P是AB的中点.
(1)如图8,若△ABC是等腰三角形,且AC=BC,在上分别取点E、F,使则有结论① ②四边形是菱形.请给出结论②的证明;
(2)如图9,若(1)中△ABC是任意三角形,其它条件不变,则(1)中的两个结论还成立吗?若成立,请给出证明;
(3)如图10,若PC是的切线,求证:
6. (2011江苏苏州,26,8分)如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB=________(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以点A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似?请写出解答过程.
7. (2011江苏泰州,26,10分)如图,以点O为圆心的两个同心圆中,矩形ABCD的边BC为大圆的弦,边AD与小圆相切于点M,OM的延长线与BC相交于点N.
(1)点N是线段BC的中点吗?为什么?
(2)若圆环的宽度(两圆半径之差)为6cm,AB=5cm,BC=10cm,求小圆的半径.
8. (2011四川成都,27,10分)已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙0,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
(1)求证:AE=CK;
(2)如果AB=,AD= (为大于零的常数),求BK的长;
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.
A
B
C
O
D
(第19题)
.
A
B
C
D
E
.
O
G
(图2)
A
B
C
D
E
F
P
.
O
G
(图1)
B
D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
——考点汇总
考点一、圆的相关概念
1、圆的定义
在一个个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径。
2、圆的几何表示
以点O为圆心的圆记作“⊙O”,读作“圆O”
考点二、弦、弧等与圆有关的定义
(1)弦
连接圆上任意两点的线段叫做弦。(如图中的AB)
(2)直径
经过圆心的弦叫做直径。(如途中的CD)
直径等于半径的2倍。
(3)半圆
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
(4)弧、优弧、劣弧
圆上任意两点间的部分叫做圆弧,简称弧。
弧用符号“⌒”表示,以A,B为端点的弧记作“”,读作“圆弧AB”或“弧AB”。
大于半圆的弧叫做优弧(多用三个字母表示);小于半圆的弧叫做劣弧(多用两个字母表示)
考点三、垂径定理及其推论
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
垂径定理及其推论可概括为:
过圆心
垂直于弦
直径 平分弦 知二推三
平分弦所对的优弧
平分弦所对的劣弧
考点四、圆的对称性
1、圆的轴对称性
圆是轴对称图形,经过圆心的每一条直线都是它的对称轴。
2、圆的中心对称性
圆是以圆心为对称中心的中心对称图形。
考点五、弧、弦、弦心距、圆心角之间的关系定理
1、圆心角
顶点在圆心的角叫做圆心角。
2、弦心距
从圆心到弦的距离叫做弦心距。
3、弧、弦、弦心距、圆心角之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦想等,所对的弦的弦心距相等。
推论:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
考点六、圆周角定理及其推论
1、圆周角
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
2、圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
考点七、点和圆的位置关系
设⊙O的半径是r,点P到圆心O的距离为d,则有:
d
d>r点P在⊙O外。
考点八、过三点的圆
1、过三点的圆
不在同一直线上的三个点确定一个圆。
2、三角形的外接圆
经过三角形的三个顶点的圆叫做三角形的外接圆。
3、三角形的外心
三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,它叫做这个三角形的外心。
4、圆内接四边形性质(四点共圆的判定条件)
圆内接四边形对角互补。
考点九、反证法
先假设命题中的结论不成立,然后由此经过推理,引出矛盾,判定所做的假设不正确,从而得到原命题成立,这种证明方法叫做反证法。
考点十、直线与圆的位置关系
直线和圆有三种位置关系,具体如下:
(1)相交:直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线,公共点叫做交点;
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,
(3)相离:直线和圆没有公共点时,叫做直线和圆相离。
如果⊙O的半径为r,圆心O到直线l的距离为d,那么:
直线l与⊙O相交d
直线l与⊙O相离d>r;
考点十一、切线的判定和性质
1、切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线。
2、切线的性质定理
圆的切线垂直于经过切点的半径。
考点十二、切线长定理
1、切线长
在经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长。
2、切线长定理
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
考点十三、三角形的内切圆
1、三角形的内切圆
与三角形的各边都相切的圆叫做三角形的内切圆。
2、三角形的内心
三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心。
考点十四、圆和圆的位置关系
1、圆和圆的位置关系
如果两个圆没有公共点,那么就说这两个圆相离,相离分为外离和内含两种。
如果两个圆只有一个公共点,那么就说这两个圆相切,相切分为外切和内切两种。
如果两个圆有两个公共点,那么就说这两个圆相交。
2、圆心距
两圆圆心的距离叫做两圆的圆心距。
3、圆和圆位置关系的性质与判定
设两圆的半径分别为R和r,圆心距为d,那么
两圆外离d>R+r
两圆外切d=R+r
两圆相交R-r
两圆内含d
4、两圆相切、相交的重要性质
如果两圆相切,那么切点一定在连心线上,它们是轴对称图形,对称轴是两圆的连心线;相交的两个圆的连心线垂直平分两圆的公共弦。
考点十五、正多边形和圆
1、正多边形的定义
各边相等,各角也相等的多边形叫做正多边形。
2、正多边形和圆的关系
只要把一个圆分成相等的一些弧,就可以做出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆。
考点十八、弧长和扇形面积
1、弧长公式
n°的圆心角所对的弧长l的计算公式为
2、扇形面积公式
其中n是扇形的圆心角度数,R是扇形的半径,l是扇形的弧长。
3、圆锥的侧面积
其中l是圆锥的母线长,r是圆锥的地面半径。
补充:
1、相交弦定理
⊙O中,弦AB与弦CD相交与点E,则AEBE=CEDE
2、弦切角定理
弦切角:圆的切线与经过切点的弦所夹的角,叫做弦切角。
弦切角定理:弦切角等于弦与切线夹的弧所对的圆周角。
即:∠BAC=∠ADC
3、切割线定理
PA为⊙O切线,PBC为⊙O割线,
则
1. (2011浙江金华,21,8分)如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE.
(1)求证:AP=AO;
(2)若tan∠OPB=,求弦AB的长;;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 ,能构成等腰梯形的四个点为 或 或 .
2. (2011山东德州22,10分)●观察计算
当,时, 与的大小关系是_________________.
当,时, 与的大小关系是_________________.
●探究证明
如图所示,为圆O的内接三角形,为直径,过C作于D,设,BD=b.
(1)分别用表示线段OC,CD ;
(2)探求OC与CD表达式之间存在的关系
(用含a,b的式子表示).
●归纳结论
根据上面的观察计算、探究证明,你能得出与的大小关系是:_________________________.
●实践应用
要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
3. (2011山东济宁,19,6分)如图,为外接圆的直径,,垂足为点,的平分线交于点,连接,.
(1) 求证:;
(2) 请判断,,三点是否在以为圆心,以为半径的圆上?并说明理由.
4. (2011山东烟台,25,12分)已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
5. (2011湖南常德,25,10分)已知 △ABC,分别以AC和BC为直径作半圆、P是AB的中点.
(1)如图8,若△ABC是等腰三角形,且AC=BC,在上分别取点E、F,使则有结论① ②四边形是菱形.请给出结论②的证明;
(2)如图9,若(1)中△ABC是任意三角形,其它条件不变,则(1)中的两个结论还成立吗?若成立,请给出证明;
(3)如图10,若PC是的切线,求证:
6. (2011江苏苏州,26,8分)如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB=________(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以点A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似?请写出解答过程.
7. (2011江苏泰州,26,10分)如图,以点O为圆心的两个同心圆中,矩形ABCD的边BC为大圆的弦,边AD与小圆相切于点M,OM的延长线与BC相交于点N.
(1)点N是线段BC的中点吗?为什么?
(2)若圆环的宽度(两圆半径之差)为6cm,AB=5cm,BC=10cm,求小圆的半径.
8. (2011四川成都,27,10分)已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙0,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
(1)求证:AE=CK;
(2)如果AB=,AD= (为大于零的常数),求BK的长;
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.
A
B
C
O
D
(第19题)
.
A
B
C
D
E
.
O
G
(图2)
A
B
C
D
E
F
P
.
O
G
(图1)
B
D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
同课章节目录
