初中数学暑期讲义——圆和圆的位置关系(无答案)
文档属性
| 名称 | 初中数学暑期讲义——圆和圆的位置关系(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-07 00:00:00 | ||
图片预览

文档简介
第八讲 圆(三)
——圆和圆的位置关系
1、定义:
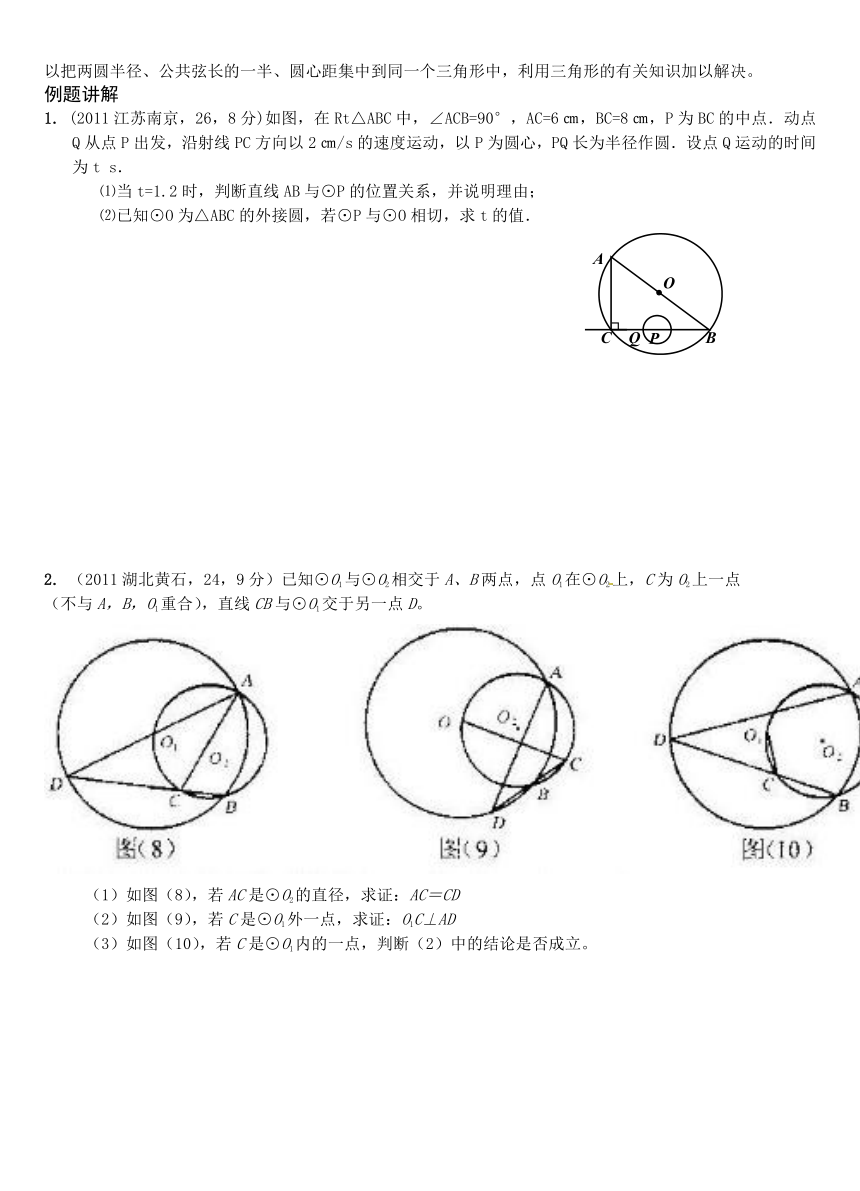
(1)如果两个圆没有公共点,那么就说这两个圆相离。
外离:两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离。(图(1))
内含:两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含(图(5))。两圆同心是两圆内含的一个特例。(图(6))
(2)如果两个圆只有一个公共点,那么就说这两个圆相切
外切:两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切。这个唯一的公共点叫做切点。(图(2))
内切:两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。这个唯一的公共点叫做切点。(图(4))
(3)两个圆有两个公共点,此时叫做这两个圆相交。(图(3))
注意:
(1)两圆外离与内含时,两圆都无公共点,但同时要考虑内部和外部的因素。两圆外切与内切也有这样的比较。
(2)两圆外切和内切统称两圆相切,即外切和内切的共性是公共点的个数唯一。
(3)两圆位置关系的五种情况也可归纳为三类:相离(外离和内含);相交;相切(外切和内切)。
2. 两圆位置关系的性质:
两圆外切d=R+r; 两圆内切d=R-r
两圆相交R-r<d<R+r; 两圆外离d>R+r;两圆内含d<R-r
为了方便记忆,将这五种数量关系用数轴表示为:
补充:
如果两个圆相切,那么切点一定在连心线上。(轴对称来说明,证明可用反证法,不作要求)
相交两圆的连心线垂直平分两圆的公共弦。
在解决有关相交两圆的问题时,常常添加以下几种辅助线:连心线、公共弦、连结交点与圆心。从而可以把两圆半径、公共弦长的一半、圆心距集中到同一个三角形中,利用三角形的有关知识加以解决。
例题讲解
1. (2011江苏南京,26,8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
2. (2011湖北黄石,24,9分)已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为O2上一点
(不与A,B,O1重合),直线CB与⊙O1交于另一点D。
(1)如图(8),若AC是⊙O2的直径,求证:AC=CD
(2)如图(9),若C是⊙O1外一点,求证:O1C⊥AD
(3)如图(10),若C是⊙O1内的一点,判断(2)中的结论是否成立。
3.(2010湖北十堰)(本小题满分9分)如图,已知⊙O1与⊙O2都过点A,AO1是⊙O2的切线,⊙O1交O1O2于点B,连结AB并延长交⊙O2于点C,连结O2C.
(1)求证:O2C⊥O1O2;
(2)证明:AB·BC=2O2B·BO1;
(3)如果AB·BC=12,O2C=4,求AO1的长.
4.(2010湖北黄石)在△ABC中,分别以AB、BC为直径⊙O、⊙O,交于另一点D.
⑴证明:交点D必在AC上;
⑵如图甲,当⊙O与⊙O半径之比为4︰3,且DO与⊙O相切时,判断△ABC的形状,并求tan∠ODB的值;
⑶如图乙,当⊙O经过点O,AB、DO的延长线交于E,且BE=BD时,求∠A的度数.
练习
一、选择题
1. (2011浙江温州,8,4分)已知线段AB=7cm.现以点A为圆心,2cm为半径画⊙A;再以点B为圆心,3cm为半径画⊙B,则⊙A和⊙B的位置关系是( )
A.内含 B.相交 C.外切 D.外离
2. (2011江苏扬州,4,3分)已知相交两圆的半径分别在4和7,则它们的圆心距可能是( )
A.2 B. 3 C. 6 D. 11
3. (2011山东济宁,5,3分)已知⊙O1与⊙O2相切,⊙O1的半径为9 cm,⊙O2的半径为2 cm,则O1O2的长是( )
A.1 cm B.5 cm C.1 cm或5 cm D.0.5cm或2.5cm
4. (2011福建泉州,5,3分)已知⊙O1和⊙O2的半径分别为2cm和5cm,两圆的圆心距是3.5cm,则两圆的位置关系是( ).
A.内含 B.外离 C.内切 D.相交
5.(2011广东茂名,7,3分)如图,⊙、⊙相内切于点A,其半径分别是8和4,将⊙沿直线平移至两圆相外切时,则点移动的长度是
A.4 B.8 C.16 D.8 或16
6. (2011湖北襄阳,9,3分)在△ABC中,∠C=90°,AC=3cm,BC=4cm,若⊙A,⊙B的半径分别为1cm,4cm,则⊙A,⊙B的位置关系是
A.外切 B.内切 C.相交 D.外离[
二、填空题
7. (2011浙江义乌,13,4分)已知⊙O1与⊙O2的半径分别为3和5,且⊙O1与⊙O2相切,则O1O2等于 .
8. (2011四川广安,14,3分)已知⊙O1与⊙O2的半径、分别是方程 的两实根,若⊙O1与⊙O2的圆心距=5.则⊙O1与⊙O2的位置关系是____
9. (2011江苏南通,18,3分)已知:如图,三个半圆以此相外切,它们的
圆心都在x轴的正半轴上并与直线y=x相切,设半圆C1、半圆C2、
半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3=
10. (2011广东肇庆,14,3分)已知两圆的半径分别为1和3,若两圆相切,则两圆的圆心距为 .
11. (2011山东枣庄,17,4分)如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0),半径为5.如果两圆内含,那么a的取值范围是________.
A
B
C
P
Q
O
O1
O2
A
B
C
D
(a,0)
x
y
O
·
3
5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
——圆和圆的位置关系
1、定义:
(1)如果两个圆没有公共点,那么就说这两个圆相离。
外离:两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离。(图(1))
内含:两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含(图(5))。两圆同心是两圆内含的一个特例。(图(6))
(2)如果两个圆只有一个公共点,那么就说这两个圆相切
外切:两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切。这个唯一的公共点叫做切点。(图(2))
内切:两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。这个唯一的公共点叫做切点。(图(4))
(3)两个圆有两个公共点,此时叫做这两个圆相交。(图(3))
注意:
(1)两圆外离与内含时,两圆都无公共点,但同时要考虑内部和外部的因素。两圆外切与内切也有这样的比较。
(2)两圆外切和内切统称两圆相切,即外切和内切的共性是公共点的个数唯一。
(3)两圆位置关系的五种情况也可归纳为三类:相离(外离和内含);相交;相切(外切和内切)。
2. 两圆位置关系的性质:
两圆外切d=R+r; 两圆内切d=R-r
两圆相交R-r<d<R+r; 两圆外离d>R+r;两圆内含d<R-r
为了方便记忆,将这五种数量关系用数轴表示为:
补充:
如果两个圆相切,那么切点一定在连心线上。(轴对称来说明,证明可用反证法,不作要求)
相交两圆的连心线垂直平分两圆的公共弦。
在解决有关相交两圆的问题时,常常添加以下几种辅助线:连心线、公共弦、连结交点与圆心。从而可以把两圆半径、公共弦长的一半、圆心距集中到同一个三角形中,利用三角形的有关知识加以解决。
例题讲解
1. (2011江苏南京,26,8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
2. (2011湖北黄石,24,9分)已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为O2上一点
(不与A,B,O1重合),直线CB与⊙O1交于另一点D。
(1)如图(8),若AC是⊙O2的直径,求证:AC=CD
(2)如图(9),若C是⊙O1外一点,求证:O1C⊥AD
(3)如图(10),若C是⊙O1内的一点,判断(2)中的结论是否成立。
3.(2010湖北十堰)(本小题满分9分)如图,已知⊙O1与⊙O2都过点A,AO1是⊙O2的切线,⊙O1交O1O2于点B,连结AB并延长交⊙O2于点C,连结O2C.
(1)求证:O2C⊥O1O2;
(2)证明:AB·BC=2O2B·BO1;
(3)如果AB·BC=12,O2C=4,求AO1的长.
4.(2010湖北黄石)在△ABC中,分别以AB、BC为直径⊙O、⊙O,交于另一点D.
⑴证明:交点D必在AC上;
⑵如图甲,当⊙O与⊙O半径之比为4︰3,且DO与⊙O相切时,判断△ABC的形状,并求tan∠ODB的值;
⑶如图乙,当⊙O经过点O,AB、DO的延长线交于E,且BE=BD时,求∠A的度数.
练习
一、选择题
1. (2011浙江温州,8,4分)已知线段AB=7cm.现以点A为圆心,2cm为半径画⊙A;再以点B为圆心,3cm为半径画⊙B,则⊙A和⊙B的位置关系是( )
A.内含 B.相交 C.外切 D.外离
2. (2011江苏扬州,4,3分)已知相交两圆的半径分别在4和7,则它们的圆心距可能是( )
A.2 B. 3 C. 6 D. 11
3. (2011山东济宁,5,3分)已知⊙O1与⊙O2相切,⊙O1的半径为9 cm,⊙O2的半径为2 cm,则O1O2的长是( )
A.1 cm B.5 cm C.1 cm或5 cm D.0.5cm或2.5cm
4. (2011福建泉州,5,3分)已知⊙O1和⊙O2的半径分别为2cm和5cm,两圆的圆心距是3.5cm,则两圆的位置关系是( ).
A.内含 B.外离 C.内切 D.相交
5.(2011广东茂名,7,3分)如图,⊙、⊙相内切于点A,其半径分别是8和4,将⊙沿直线平移至两圆相外切时,则点移动的长度是
A.4 B.8 C.16 D.8 或16
6. (2011湖北襄阳,9,3分)在△ABC中,∠C=90°,AC=3cm,BC=4cm,若⊙A,⊙B的半径分别为1cm,4cm,则⊙A,⊙B的位置关系是
A.外切 B.内切 C.相交 D.外离[
二、填空题
7. (2011浙江义乌,13,4分)已知⊙O1与⊙O2的半径分别为3和5,且⊙O1与⊙O2相切,则O1O2等于 .
8. (2011四川广安,14,3分)已知⊙O1与⊙O2的半径、分别是方程 的两实根,若⊙O1与⊙O2的圆心距=5.则⊙O1与⊙O2的位置关系是____
9. (2011江苏南通,18,3分)已知:如图,三个半圆以此相外切,它们的
圆心都在x轴的正半轴上并与直线y=x相切,设半圆C1、半圆C2、
半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3=
10. (2011广东肇庆,14,3分)已知两圆的半径分别为1和3,若两圆相切,则两圆的圆心距为 .
11. (2011山东枣庄,17,4分)如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0),半径为5.如果两圆内含,那么a的取值范围是________.
A
B
C
P
Q
O
O1
O2
A
B
C
D
(a,0)
x
y
O
·
3
5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
同课章节目录
