华师大版八年级数学上册第14章《勾股定理》章末检测(Word版 含答案)
文档属性
| 名称 | 华师大版八年级数学上册第14章《勾股定理》章末检测(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 236.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 19:42:01 | ||
图片预览



文档简介
章末检测
一、选择题(每题3分,共30分)
1.在Rt△ABC中,∠C=90°,a,b,c分别表示∠A,∠B,∠C的对边,则下列各式中不正确的是( )
A.a2+b2=c2
B.c2-a2=b2
C.a2-b2=c2
D.c2-b2=a2
2.用反证法证明“如果在△ABC中,∠C=90°,那么∠A,∠B中至少有一个角不大于45°”时,应先假设( )
A.∠A>45°,∠B>45°
B.∠A≥45°,∠B≥45°
C.∠A<45°,∠B<45°
D.∠A≤45°,∠B≤45°
3.若直角三角形的两直角边长各扩大为原来的3倍,则其斜边长扩大为原来的( )
A.1倍
B.2倍
C.3倍
D.4倍
4.已知一个直角三角形的面积为96,并且两直角边长的比为3:4,则这个三角形的斜边长为( )
A.10
B.20
C.5
D.15
5.下列各组数为勾股数的是( )
A.6,12,13
B.3,4,7
C.8,15,17
D.0.9,1.2,1.5
6.如图,在一块平地上,张大爷家屋前9米远处有一棵大树,在一次强风中,这棵大树从离地面6米处朝张大爷的房子方向折断倒下,量得倒下部分的长是10米,大树倒下时会砸到张大爷的房子吗?( )
A.一定不会
B.可能会
C.一定会
D.以上都不对
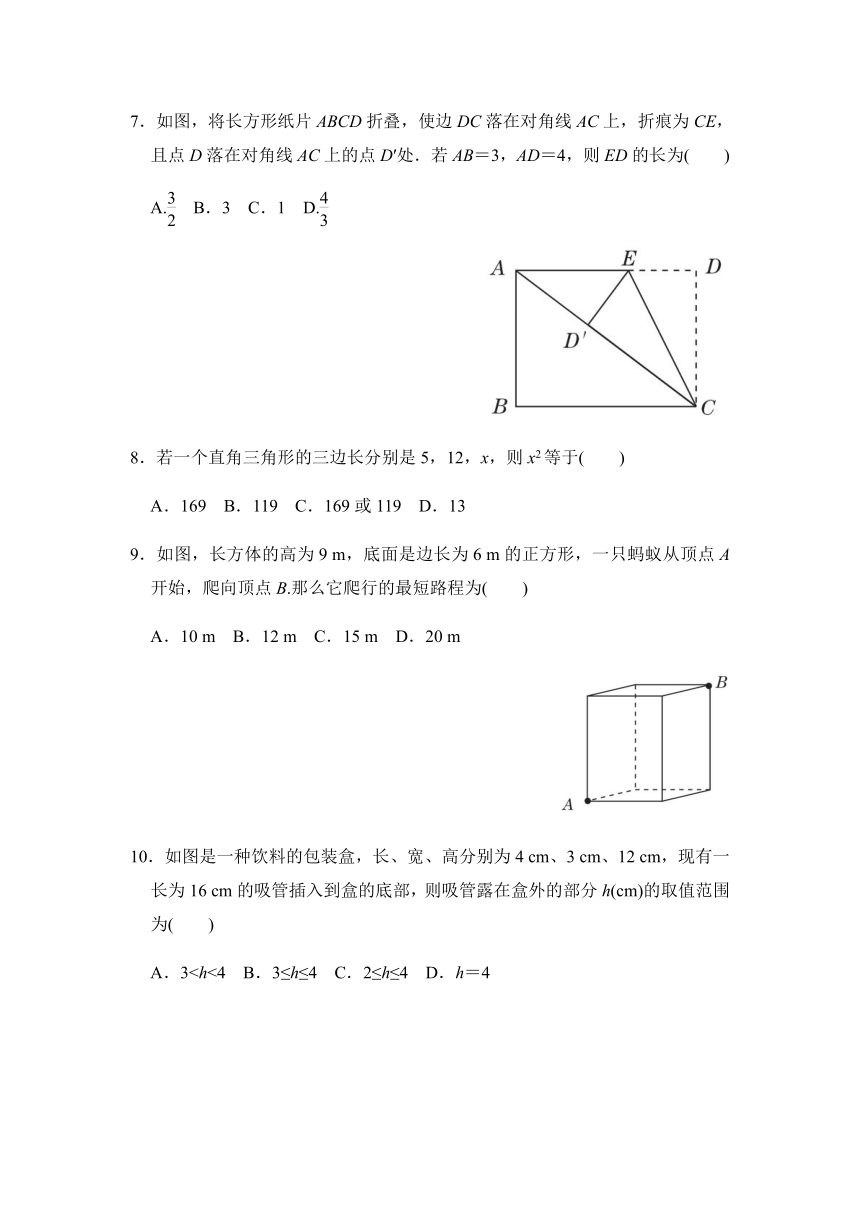
7.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且点D落在对角线AC上的点D′处.若AB=3,AD=4,则ED的长为( )
A.
B.3
C.1
D.
8.若一个直角三角形的三边长分别是5,12,x,则x2等于( )
A.169
B.119
C.169或119
D.13
9.如图,长方体的高为9
m,底面是边长为6
m的正方形,一只蚂蚁从顶点A开始,爬向顶点B.那么它爬行的最短路程为( )
A.10
m
B.12
m
C.15
m
D.20
m
10.如图是一种饮料的包装盒,长、宽、高分别为4
cm、3
cm、12
cm,现有一长为16
cm的吸管插入到盒的底部,则吸管露在盒外的部分h(cm)的取值范围为( )
A.3B.3≤h≤4
C.2≤h≤4
D.h=4
二、填空题(每题3分,共30分)
11.若用反证法证明“有两个内角不相等的三角形不是等边三角形”,可先假设这个三角形是________.
12.在△ABC中,AC2-AB2=BC2,则∠B的度数为________.
13.已知一个直角三角形木板三边长的平方和为1
800,则斜边长为________.
14.若一个三角形的三边之比为3:4:5,且周长为24
cm,则它的面积为________cm2.
15.飞机在空中水平飞行,某一时刻刚好飞到一个男孩正上方4
000
m处,过了10
s,飞机距离这个男孩头顶5
000
m,则飞机平均每小时飞行__________km.
16.已知a,b,c是△ABC的三边长,且满足关系+|a-b|=0,则△ABC的形状为____________.
17.如图,每个小方格的边长为1.若一束光线从点A出发,经过直线MN上一点反射后经过点B,则光线从点A到点B经过的路线长是________.
18.如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是________(结果精确到0.01).
19.如图,圆柱形无盖容器高为18
cm,底面周长为24
cm,在容器内壁离容器底4
cm的点B处有一滴蜂蜜,此时蚂蚁正好在容器外壁,离容器上沿2
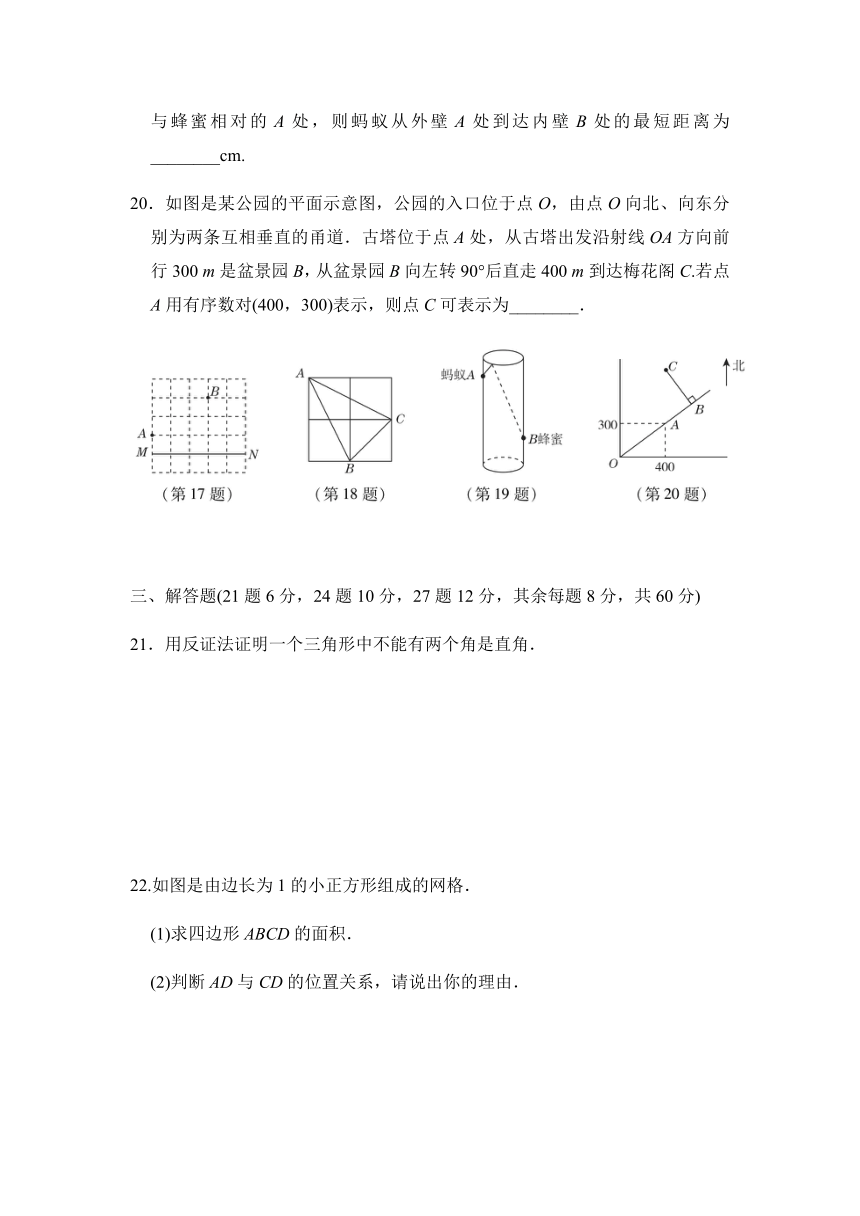
cm与蜂蜜相对的A处,则蚂蚁从外壁A处到达内壁B处的最短距离为________cm.
20.如图是某公园的平面示意图,公园的入口位于点O,由点O向北、向东分别为两条互相垂直的甬道.古塔位于点A处,从古塔出发沿射线OA方向前行300
m是盆景园B,从盆景园B向左转90°后直走400
m到达梅花阁C.若点A用有序数对(400,300)表示,则点C可表示为________.
三、解答题(21题6分,24题10分,27题12分,其余每题8分,共60分)
21.用反证法证明一个三角形中不能有两个角是直角.
22.如图是由边长为1的小正方形组成的网格.
(1)求四边形ABCD的面积.
(2)判断AD与CD的位置关系,请说出你的理由.
23.若△ABC的三边长a,b,c满足a2+b2+c2+50=6a+8b+10c,判断△ABC的形状.
24.我们把满足x2+y2=z2的正整数x,y,z叫做勾股数,如3,4,5就是一组勾股数.
(1)请你再写出两组勾股数:________,________;
(2)在研究勾股数时,古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2-1,z=n2+1,那么以x,y,z为三边长的三角形为直角三角形(即x,y,z为勾股数),请你加以证明.
25.如图,∠ABC=90°,AB=6
cm,AD=24
cm,BC+CD=34
cm,C是直线l上一动点,请你探索当点C离点B多远时,△ACD是一个以CD为斜边的直角三角形.
26.如图,在梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.求AB的长(提示:在直角三角形中,30°角所对的直角边等于斜边的一半).
27.“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN上限速60千米/时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
答案
一、1.C 2.A 3.C 4.B 5.C 6.A 7.A 8.C 9.C 10.B
二、11.等边三角形
12.90° 13.30 14.24 15.1
080
16.等腰直角三角形 点拨:由题意知c2-a2-b2=0,且a-b=0,∴a2+b2=c2,且a=b.
∴△ABC为等腰直角三角形.
17.5
18.2.12 点拨:在网格中求三角形的高,应借助三角形的面积求解.以AC,AB,BC为斜边的三个直角三角形的面积分别为1,1,,因此△ABC的面积为2×2-1-1-=;用勾股定理计算出BC的长为,因此BC
边上的高约为2.12.
19.20
20.(400,800) 点拨:如图,连结AC.由题意可得OA=500
m,AB=300
m,BC=400
m.在△AOD和△ACB中,AD=AB,∠ODA=∠ABC=90°,OD=CB,∴△AOD≌△ACB(S.A.S.),∴AC=AO=500
m,∠CAB=∠OAD.
∵点B,A,O在一条直线上,∴点C,A,D也在一条直线上,∴CD=AC+AD=800
m,∴点C可表示为(400,800).
三、21.证明:假设三角形ABC的三个内角∠A、∠B、∠C中有两个直角,不妨设∠A=∠B=90°,则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,所以∠A=∠B=90°不成立,所以一个三角形中不能有两个角是直角.
22.解:(1)如图,将四边形ABCD分成4个小直角三角形,发现每个小直角三角形的面积恰好是以小直角三角形的斜边为对角线的长方形(正方形)面积的一半,因此四边形ABCD的面积为整个网格面积的一半,即四边形ABCD的面积为×52=12.5.
(2)AD⊥CD.理由如下:
在△ADC中,因为AD2=12+22=5,
CD2=22+42=20,AC2=52=25,
∴AD2+CD2=AC2,
∴△ADC是直角三角形,且∠ADC=90°,
∴AD⊥CD.
23.解:∵a2+b2+c2+50=6a+8b+10c,
∴a2+b2+c2-6a-8b-10c+50=0,即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5.
∵32+42=52,即a2+b2=c2,
∴根据勾股定理的逆定理可判定△ABC是直角三角形.
点拨:本题利用配方法,先求出a,b,c的值,再利用勾股定理的逆定理进行判断.
24.(1)6,8,10;9,12,15(答案不唯一)
(2)证明:∵x2+y2=(2n)2+(n2-1)2=4n2+n4-2n2+1=n4+2n2+1=(n2+1)2=z2,
∴以x,y,z为三边长的三角形为直角三角形.
25.解:设当BC=x
cm时,△ACD是一个以CD为斜边的直角三角形.
∵BC+CD=34
cm,
∴CD=(34-x)cm.
∵∠ABC=90°,AB=6
cm,
∴在Rt△ABC中,由勾股定理得AC2=AB2+BC2=36+x2.
在Rt△ACD中,AD=24
cm,由勾股定理得AC2=CD2-AD2=(34-x)2-576,
∴36+x2=(34-x)2-576,
解得x=8.
∴当点C离点B
8
cm时,△ACD是一个以CD为斜边的直角三角形.
26.解:∵BF=CF=8,∠C=30°,
∴∠FBC=∠C=30°,∴∠DFB=60°.由题易知BE与BC关于直线BF对称,
∴∠DBF=∠FBC=30°,
∴∠BDC=90°.∴DF=BF=4,
∴BD2=BF2-DF2=64-16=48.
∵∠A=90°,AD∥BC,∴∠ABC=90°,
∴∠ABD=30°,∴AD=BD,
∴AB2=BD2-AD2=BD2-=BD2=×48=36.∴AB=6.
27.解:此车没有超速.理由如下:如图,过点C作CH⊥MN于H,
∵∠CBH=60°,∴∠BCH=30°.又BC=200米,∴BH=BC=100米,∴CH==≈173(米).
∵∠CAH=45°,∠CHA=90°,
∴AH=CH≈173米.
∴AB≈173-100=73(米).
∴小车的速度约为73÷5=(米/秒).
又∵60千米/时=米/秒,<,∴此车没有超速.
一、选择题(每题3分,共30分)
1.在Rt△ABC中,∠C=90°,a,b,c分别表示∠A,∠B,∠C的对边,则下列各式中不正确的是( )
A.a2+b2=c2
B.c2-a2=b2
C.a2-b2=c2
D.c2-b2=a2
2.用反证法证明“如果在△ABC中,∠C=90°,那么∠A,∠B中至少有一个角不大于45°”时,应先假设( )
A.∠A>45°,∠B>45°
B.∠A≥45°,∠B≥45°
C.∠A<45°,∠B<45°
D.∠A≤45°,∠B≤45°
3.若直角三角形的两直角边长各扩大为原来的3倍,则其斜边长扩大为原来的( )
A.1倍
B.2倍
C.3倍
D.4倍
4.已知一个直角三角形的面积为96,并且两直角边长的比为3:4,则这个三角形的斜边长为( )
A.10
B.20
C.5
D.15
5.下列各组数为勾股数的是( )
A.6,12,13
B.3,4,7
C.8,15,17
D.0.9,1.2,1.5
6.如图,在一块平地上,张大爷家屋前9米远处有一棵大树,在一次强风中,这棵大树从离地面6米处朝张大爷的房子方向折断倒下,量得倒下部分的长是10米,大树倒下时会砸到张大爷的房子吗?( )
A.一定不会
B.可能会
C.一定会
D.以上都不对
7.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且点D落在对角线AC上的点D′处.若AB=3,AD=4,则ED的长为( )
A.
B.3
C.1
D.
8.若一个直角三角形的三边长分别是5,12,x,则x2等于( )
A.169
B.119
C.169或119
D.13
9.如图,长方体的高为9
m,底面是边长为6
m的正方形,一只蚂蚁从顶点A开始,爬向顶点B.那么它爬行的最短路程为( )
A.10
m
B.12
m
C.15
m
D.20
m
10.如图是一种饮料的包装盒,长、宽、高分别为4
cm、3
cm、12
cm,现有一长为16
cm的吸管插入到盒的底部,则吸管露在盒外的部分h(cm)的取值范围为( )
A.3
C.2≤h≤4
D.h=4
二、填空题(每题3分,共30分)
11.若用反证法证明“有两个内角不相等的三角形不是等边三角形”,可先假设这个三角形是________.
12.在△ABC中,AC2-AB2=BC2,则∠B的度数为________.
13.已知一个直角三角形木板三边长的平方和为1
800,则斜边长为________.
14.若一个三角形的三边之比为3:4:5,且周长为24
cm,则它的面积为________cm2.
15.飞机在空中水平飞行,某一时刻刚好飞到一个男孩正上方4
000
m处,过了10
s,飞机距离这个男孩头顶5
000
m,则飞机平均每小时飞行__________km.
16.已知a,b,c是△ABC的三边长,且满足关系+|a-b|=0,则△ABC的形状为____________.
17.如图,每个小方格的边长为1.若一束光线从点A出发,经过直线MN上一点反射后经过点B,则光线从点A到点B经过的路线长是________.
18.如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是________(结果精确到0.01).
19.如图,圆柱形无盖容器高为18
cm,底面周长为24
cm,在容器内壁离容器底4
cm的点B处有一滴蜂蜜,此时蚂蚁正好在容器外壁,离容器上沿2
cm与蜂蜜相对的A处,则蚂蚁从外壁A处到达内壁B处的最短距离为________cm.
20.如图是某公园的平面示意图,公园的入口位于点O,由点O向北、向东分别为两条互相垂直的甬道.古塔位于点A处,从古塔出发沿射线OA方向前行300
m是盆景园B,从盆景园B向左转90°后直走400
m到达梅花阁C.若点A用有序数对(400,300)表示,则点C可表示为________.
三、解答题(21题6分,24题10分,27题12分,其余每题8分,共60分)
21.用反证法证明一个三角形中不能有两个角是直角.
22.如图是由边长为1的小正方形组成的网格.
(1)求四边形ABCD的面积.
(2)判断AD与CD的位置关系,请说出你的理由.
23.若△ABC的三边长a,b,c满足a2+b2+c2+50=6a+8b+10c,判断△ABC的形状.
24.我们把满足x2+y2=z2的正整数x,y,z叫做勾股数,如3,4,5就是一组勾股数.
(1)请你再写出两组勾股数:________,________;
(2)在研究勾股数时,古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2-1,z=n2+1,那么以x,y,z为三边长的三角形为直角三角形(即x,y,z为勾股数),请你加以证明.
25.如图,∠ABC=90°,AB=6
cm,AD=24
cm,BC+CD=34
cm,C是直线l上一动点,请你探索当点C离点B多远时,△ACD是一个以CD为斜边的直角三角形.
26.如图,在梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.求AB的长(提示:在直角三角形中,30°角所对的直角边等于斜边的一半).
27.“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN上限速60千米/时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
答案
一、1.C 2.A 3.C 4.B 5.C 6.A 7.A 8.C 9.C 10.B
二、11.等边三角形
12.90° 13.30 14.24 15.1
080
16.等腰直角三角形 点拨:由题意知c2-a2-b2=0,且a-b=0,∴a2+b2=c2,且a=b.
∴△ABC为等腰直角三角形.
17.5
18.2.12 点拨:在网格中求三角形的高,应借助三角形的面积求解.以AC,AB,BC为斜边的三个直角三角形的面积分别为1,1,,因此△ABC的面积为2×2-1-1-=;用勾股定理计算出BC的长为,因此BC
边上的高约为2.12.
19.20
20.(400,800) 点拨:如图,连结AC.由题意可得OA=500
m,AB=300
m,BC=400
m.在△AOD和△ACB中,AD=AB,∠ODA=∠ABC=90°,OD=CB,∴△AOD≌△ACB(S.A.S.),∴AC=AO=500
m,∠CAB=∠OAD.
∵点B,A,O在一条直线上,∴点C,A,D也在一条直线上,∴CD=AC+AD=800
m,∴点C可表示为(400,800).
三、21.证明:假设三角形ABC的三个内角∠A、∠B、∠C中有两个直角,不妨设∠A=∠B=90°,则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,所以∠A=∠B=90°不成立,所以一个三角形中不能有两个角是直角.
22.解:(1)如图,将四边形ABCD分成4个小直角三角形,发现每个小直角三角形的面积恰好是以小直角三角形的斜边为对角线的长方形(正方形)面积的一半,因此四边形ABCD的面积为整个网格面积的一半,即四边形ABCD的面积为×52=12.5.
(2)AD⊥CD.理由如下:
在△ADC中,因为AD2=12+22=5,
CD2=22+42=20,AC2=52=25,
∴AD2+CD2=AC2,
∴△ADC是直角三角形,且∠ADC=90°,
∴AD⊥CD.
23.解:∵a2+b2+c2+50=6a+8b+10c,
∴a2+b2+c2-6a-8b-10c+50=0,即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5.
∵32+42=52,即a2+b2=c2,
∴根据勾股定理的逆定理可判定△ABC是直角三角形.
点拨:本题利用配方法,先求出a,b,c的值,再利用勾股定理的逆定理进行判断.
24.(1)6,8,10;9,12,15(答案不唯一)
(2)证明:∵x2+y2=(2n)2+(n2-1)2=4n2+n4-2n2+1=n4+2n2+1=(n2+1)2=z2,
∴以x,y,z为三边长的三角形为直角三角形.
25.解:设当BC=x
cm时,△ACD是一个以CD为斜边的直角三角形.
∵BC+CD=34
cm,
∴CD=(34-x)cm.
∵∠ABC=90°,AB=6
cm,
∴在Rt△ABC中,由勾股定理得AC2=AB2+BC2=36+x2.
在Rt△ACD中,AD=24
cm,由勾股定理得AC2=CD2-AD2=(34-x)2-576,
∴36+x2=(34-x)2-576,
解得x=8.
∴当点C离点B
8
cm时,△ACD是一个以CD为斜边的直角三角形.
26.解:∵BF=CF=8,∠C=30°,
∴∠FBC=∠C=30°,∴∠DFB=60°.由题易知BE与BC关于直线BF对称,
∴∠DBF=∠FBC=30°,
∴∠BDC=90°.∴DF=BF=4,
∴BD2=BF2-DF2=64-16=48.
∵∠A=90°,AD∥BC,∴∠ABC=90°,
∴∠ABD=30°,∴AD=BD,
∴AB2=BD2-AD2=BD2-=BD2=×48=36.∴AB=6.
27.解:此车没有超速.理由如下:如图,过点C作CH⊥MN于H,
∵∠CBH=60°,∴∠BCH=30°.又BC=200米,∴BH=BC=100米,∴CH==≈173(米).
∵∠CAH=45°,∠CHA=90°,
∴AH=CH≈173米.
∴AB≈173-100=73(米).
∴小车的速度约为73÷5=(米/秒).
又∵60千米/时=米/秒,<,∴此车没有超速.
