鲁教版(五四制)八年级数学上册《第4章 图形的平移与旋转》 单元测试卷 (Word版 含解析)
文档属性
| 名称 | 鲁教版(五四制)八年级数学上册《第4章 图形的平移与旋转》 单元测试卷 (Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 428.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 00:00:00 | ||
图片预览


文档简介
第4章
图形的平移与旋转
一、选择题(每小题3分,共30分)
1.下列图形中,既是中心对称图形,又是轴对称图形的是( )
A.
B.
C.
D.
2.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
3.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(﹣2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再把△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1,则点A的对应点A2的坐标是( )
A.(5,2)
B.(1,0)
C.(3,﹣1)
D.(5,﹣2)
4.如图,∠C=90°,AC=4,BC=3,△ADE由△ABC旋转而成,则BE的长为( )
A.1
B.
C.1.2
D.2
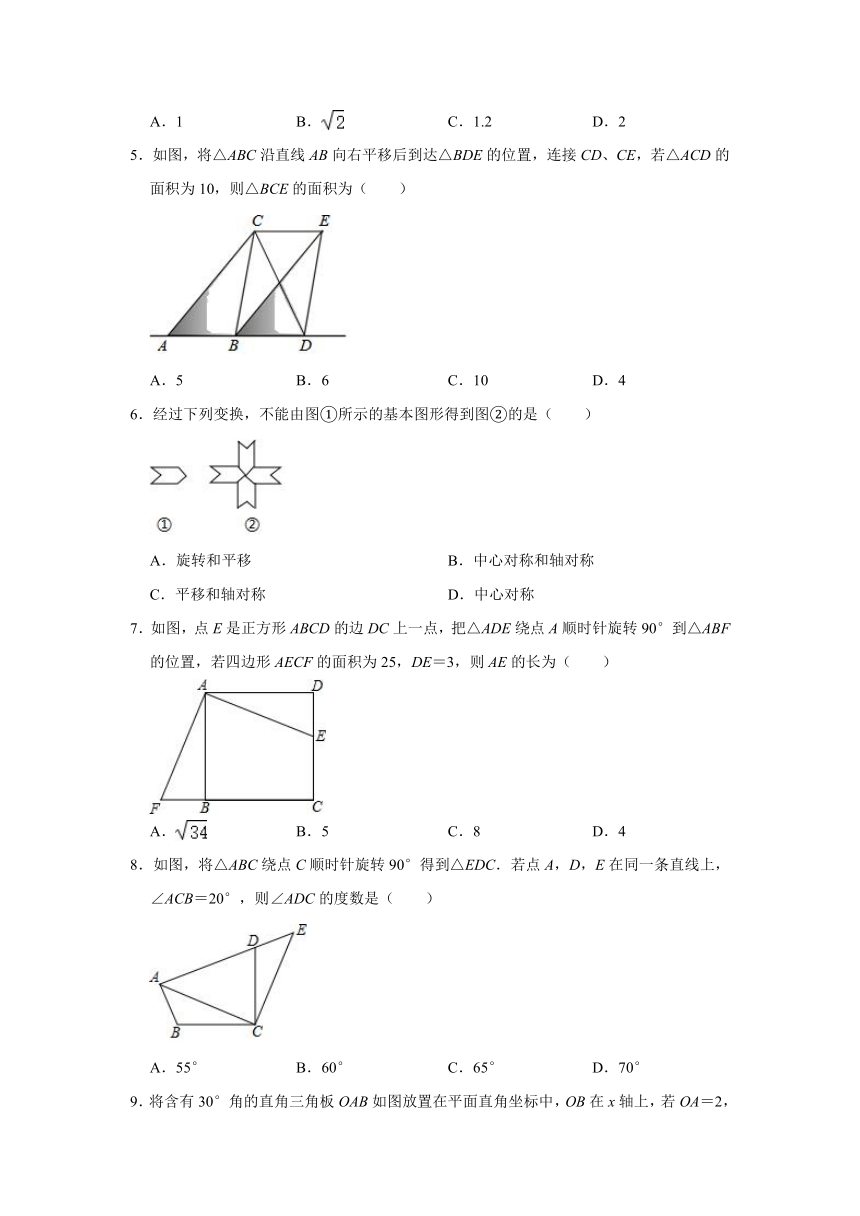
5.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为10,则△BCE的面积为( )
A.5
B.6
C.10
D.4
6.经过下列变换,不能由图①所示的基本图形得到图②的是( )
A.旋转和平移
B.中心对称和轴对称
C.平移和轴对称
D.中心对称
7.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=3,则AE的长为( )
A.
B.5
C.8
D.4
8.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
9.将含有30°角的直角三角板OAB如图放置在平面直角坐标中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A.(,1)
B.(1,﹣)
C.(,﹣)
D.(﹣,)
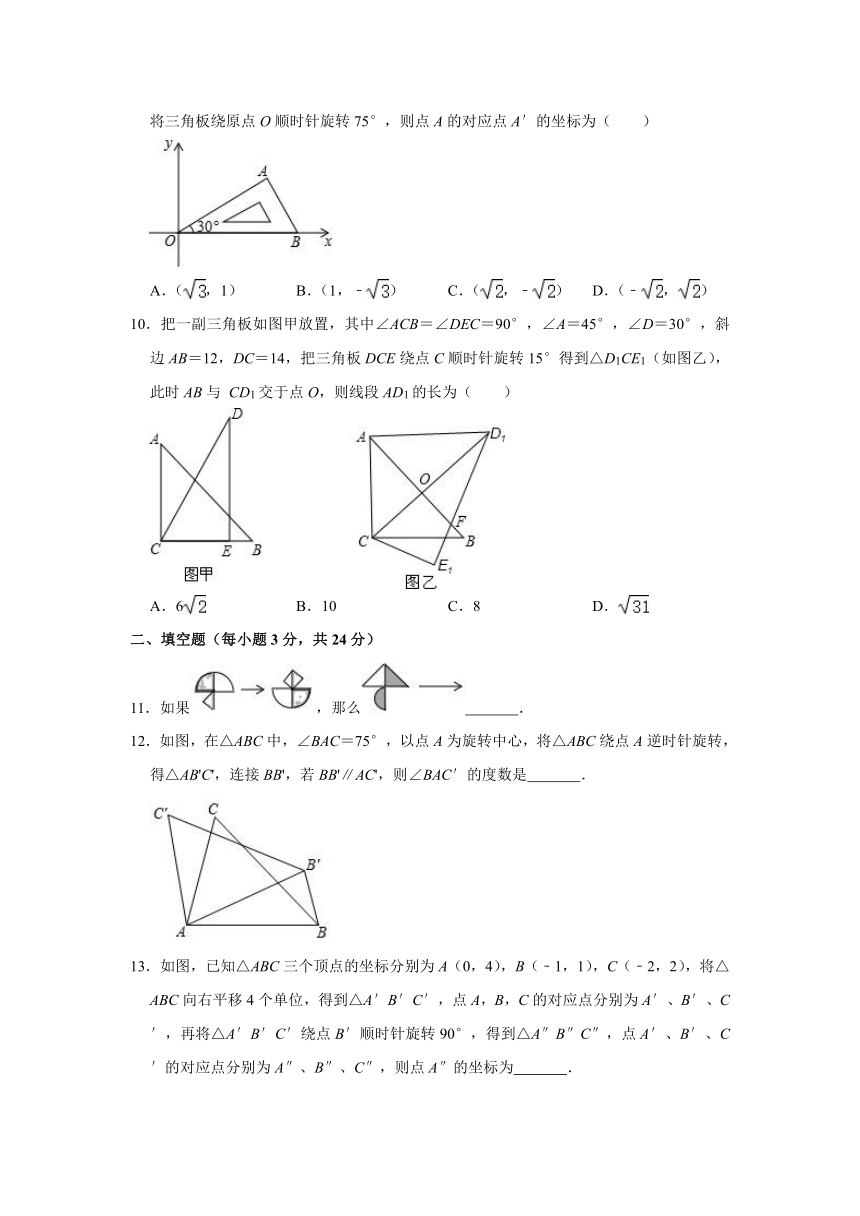
10.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与
CD1交于点O,则线段AD1的长为( )
A.6
B.10
C.8
D.
二、填空题(每小题3分,共24分)
11.如果,那么
.
12.如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′的度数是
.
13.如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为
.
14.如图,Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,下列结论:
①△ABC≌△DEF;②∠DEF=90°;③AC=DF;④EC=CF;⑤S四动形ABEG=S四边形DGCF.其中正确的有
(填序号).
15.边长为1的正方形网格在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为A(3,3),B(5,0),若A1的坐标为(﹣5,﹣3),则B1的坐标为
.
16.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为
.
17.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB′C′,点B、C的对应点分别为点B'、C′,AB′与BC相交于点D,当B′C′∥AB时,则CD=
.
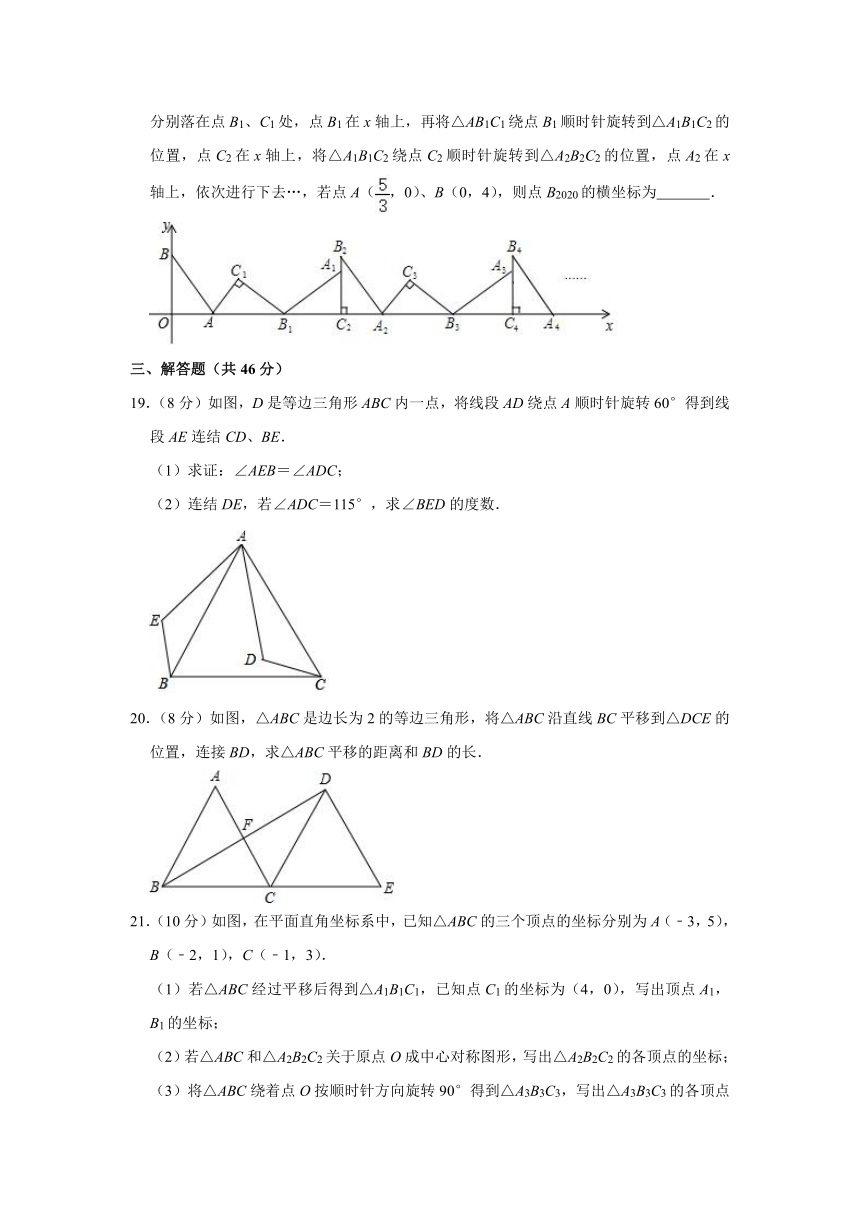
18.如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(,0)、B(0,4),则点B2020的横坐标为
.
三、解答题(共46分)
19.(8分)如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°得到线段AE连结CD、BE.
(1)求证:∠AEB=∠ADC;
(2)连结DE,若∠ADC=115°,求∠BED的度数.
20.(8分)如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
21.(10分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
22.(10分)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
23.(10分)已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.下列图形中,既是中心对称图形,又是轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、不是中心对称图形,不是轴对称图形,故此选项不合题意;
B、既是中心对称图形,又是轴对称图形,故此选项符合题意;
C、不是中心对称图形,是轴对称图形,故此选项不合题意;
D、是中心对称图形,不是轴对称图形,故此选项不合题意;
故选:B.
2.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
【分析】根据图形的对称性,用360°除以3计算即可得解.
【解答】解:∵360°÷3=120°,
∴旋转的角度是120°的整数倍,
∴旋转的角度至少是120°.
故选:C.
3.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(﹣2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再把△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1,则点A的对应点A2的坐标是( )
A.(5,2)
B.(1,0)
C.(3,﹣1)
D.(5,﹣2)
【分析】根据平移变换,旋转变换的性质画出图象即可解决问题;
【解答】解:如图,△A2B2C1即为所求.
观察图象可知:A2(5,2)
故选:A.
4.如图,∠C=90°,AC=4,BC=3,△ADE由△ABC旋转而成,则BE的长为( )
A.1
B.
C.1.2
D.2
【分析】根据BE=AB﹣AE,求出AB,AE即可解决问题;
【解答】解:在Rt△ABC中,∵∠C=90°,AC=4,BC=3,
∴AB==5,
由旋转不变性可知:AE=AC=4,
∴BE=AB﹣AE=5﹣4=1,
故选:A.
5.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为10,则△BCE的面积为( )
A.5
B.6
C.10
D.4
【分析】根据平移的性质得到AB=BD,BC∥DE,利用三角形面积公式得到S△BCD=S△ACD=5,然后利用DE∥BC得到S△BCE=S△BCD=5.
【解答】解:∵△ABC沿直线AB向右平移后到达△BDE的位置,
∴AB=BD,BC∥DE,
∴S△ABC=S△BCD=S△ACD=×10=5,
∵DE∥BC,
∴S△BCE=S△BCD=5.
故选:A.
6.经过下列变换,不能由图①所示的基本图形得到图②的是( )
A.旋转和平移
B.中心对称和轴对称
C.平移和轴对称
D.中心对称
【分析】根据旋转、平移、轴对称、中心对称的性质即可进行逐一判断.
【解答】解:因为经过旋转和平移能由图①所示的基本图形得到图②,所以A选项不符合题意;
因为经过中心对称和轴对称能由图①所示的基本图形得到图②,所以B选项不符合题意;
因为经过平移和轴对称能由图①所示的基本图形得到图②,所以C选项不符合题意;
因为经过中心对称不能由图①所示的基本图形得到图②,所以D选项符合题意.
故选:D.
7.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=3,则AE的长为( )
A.
B.5
C.8
D.4
【分析】利用旋转的性质得出四边形AECF的面积等于正方形ABCD的面积,进而可求出正方形的边长,再利用勾股定理得出答案.
【解答】解:∵把△ADE顺时针旋转△ABF的位置,
∴四边形AECF的面积等于正方形ABCD的面积等于25,
∴AD=DC=5,
∵DE=3,
∴Rt△ADE中,AE===.
故选:A.
8.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
【分析】根据旋转的性质和三角形内角和解答即可.
【解答】解:∵将△ABC绕点C顺时针旋转90°得到△EDC.
∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,
∴∠CAD=45°,∠ACD=90°﹣20°=70°,
∴∠ADC=180°﹣45°﹣70°=65°,
故选:C.
9.将含有30°角的直角三角板OAB如图放置在平面直角坐标中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A.(,1)
B.(1,﹣)
C.(,﹣)
D.(﹣,)
【分析】求出旋转后OA与y轴夹角为45°,然后求出点A′的横坐标与纵坐标,从而得解.
【解答】解:如图,
∵三角板绕原点O顺时针旋转75°,
∴旋转后OA与y轴夹角为45°,
∵OA=2,
∴OA′=2,
∴点A′的横坐标为2×=,
纵坐标为﹣2×=﹣,
所以,点A′的坐标为(,﹣).
故选:C.
10.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与
CD1交于点O,则线段AD1的长为( )
A.6
B.10
C.8
D.
【分析】先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°,然后判断出△ACO是等腰直角三角形,再根据等腰直角三角形的性质求出AO、CO,AB⊥CO,再求出OD1然后利用勾股定理列式计算即可得解.
【解答】解:∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°﹣30°=60°,
∴∠ACD=90°﹣60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°,
又∵∠A=45°,
∴△ACO是等腰直角三角形,
∴AO=CO=AB=×12=6,AB⊥CO,
∵DC=14,
∴D1C=DC=14,
∴D1O=14﹣6=8,
在Rt△AOD1中,AD1===10.
故选:B.
二、填空题(每小题3分,共24分)
11.如果,那么 .
【分析】观察图象的变化,根据旋转变换的性质轴对称的性质即可解决问题.
【解答】解:由题意性质180,可得图形:
12.如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′的度数是 105° .
【分析】由旋转的性质可得∠BAC=∠B'AC'=75°,AB=AB',由平行线的性质和等腰三角形的性质可得∠BAB'=30°,即可求解.
【解答】解:∵以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',
∴∠BAC=∠B'AC'=75°,AB=AB',
∵BB'∥AC',
∴∠C'AB'=∠AB'B=75°,
∵AB=AB',
∴∠AB'B=∠BB'A=75°,
∴∠BAB'=30°,
∴∠BAC'=∠BAB'+∠B'A'C'=75°+30°=105°,
故答案为:105°.
13.如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为 (6,0) .
【分析】由平移的性质和旋转的性质作出图形,即可得出答案.
【解答】解:如图所示:
∵A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,
∴A′、B′、C′的坐标分别为(4,4),B(3,1),C(2,2),
再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,
则点A″的坐标为
(6,0);
故答案为:(6,0).
14.如图,Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,下列结论:
①△ABC≌△DEF;②∠DEF=90°;③AC=DF;④EC=CF;⑤S四动形ABEG=S四边形DGCF.其中正确的有 ①②③⑤ (填序号).
【分析】由平移的性质可得Rt△ABC≌△Rt△DEF,由全等三角形的性质依次判断可求解.
【解答】解:∵Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,
∴Rt△ABC≌△Rt△DEF,故①正确;
∴S△ABC=S△DEF,∠ABC=∠DEF=90°,BC=EF,AC=DF,故②、③正确;
∴S四动形ABEG=S四边形DGCF,CF=BE,故④错误,⑤正确,
故答案为:①②③⑤.
15.边长为1的正方形网格在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为A(3,3),B(5,0),若A1的坐标为(﹣5,﹣3),则B1的坐标为 (﹣3,﹣6) .
【分析】各对应点之间的关系是横坐标加﹣8,纵坐标加﹣6,那么让点B的横坐标加﹣8,纵坐标加﹣6即为点B1的坐标.
【解答】解:由点A到A1可知:各对应点之间的关系是横坐标加﹣8,纵坐标加﹣6,那点B到B1的移动规律也如此,则B1的横坐标为5+(﹣8)=﹣3;纵坐标为0+(﹣6)=﹣6;
∴B1的坐标为(﹣3,﹣6).
故答案为:(﹣3,﹣6).
16.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 6 .
【分析】根据中心对称图形的概念,以及长方形的面积公式即可解答.
【解答】解:∵直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D,OB=3,OD=2,
∴AB=2,
∴阴影部分的面积之和为3×2=6.
故答案为:6.
17.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB′C′,点B、C的对应点分别为点B'、C′,AB′与BC相交于点D,当B′C′∥AB时,则CD= .
【分析】设CD=x,由B′C′∥AB,可推得∠BAD=∠B′,由旋转的性质得:∠B=∠B′,于是得到∠BAD=∠B,AC=AC′=4,AD=BD=8﹣x,由勾股定理可求解.
【解答】解:设CD=x,
∵B′C′∥AB,
∴∠BAD=∠B′,
由旋转的性质得:∠B=∠B′,AC=AC′=6,
∴∠BAD=∠B,
∴AD=BD=8﹣x,
∴(8﹣x)2=x2+62,
∴x=,
∴CD=,
故答案为:.
18.如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(,0)、B(0,4),则点B2020的横坐标为 10100 .
【分析】首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…,即可得每偶数之间的B相差10个单位长度,根据这个规律可以求得B2020的坐标.
【解答】解:由图象可知点B2020在第一象限,
∵OA=,OB=4,∠AOB=90°,
∴AB===,
∴B2(10,4),B4(20,4),B6(30,4),…
∴B2020(10100,4).
∴点B2020横坐标为10100.
故答案为10100
三、解答题(共46分)
19.(8分)如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°得到线段AE连结CD、BE.
(1)求证:∠AEB=∠ADC;
(2)连结DE,若∠ADC=115°,求∠BED的度数.
【分析】(1)由等边三角形的性质知∠BAC=60°,AB=AC,由旋转的性质知∠DAE=60°,AE=AD,从而得∠EAB=∠DAC,再证△EAB≌△DAC可得答案;
(2)由∠DAE=60°,AE=AD知△EAD为等边三角形,即∠AED=60°,继而由∠AEB=∠ADC=115°可得.
【解答】解:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
,
∴△EAB≌△DAC(SAS),
∴∠AEB=∠ADC;
(2)如图,
∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形.
∴∠AED=60°,
又∵∠AEB=∠ADC=115°.
∴∠BED=55°.
20.(8分)如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
【分析】由平移的性质可知△ABC平移的距离,以及BE=2BC=4,DE=AC=2,故可得出BD⊥DE,由∠E=∠ACB=60°,在Rt△BDE中利用勾股定理即可得出BD的长.
【解答】解:∵△DCE由△ABC平移而成,
∴△ABC平移的距离为:BC=2,
且BE=2BC=4,DE=AC=2,∠E=∠ACB=60°,
∴DE=BE,
∴BD⊥DE,
又∵∠E=∠ACB=60°,
∴AC∥DE,
∴BD⊥AC,
∴△BED是直角三角形,
∵BE=4,DE=2,
∴BD==2.
21.(10分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
【分析】(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
【解答】解:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
22.(10分)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【分析】(1)根据题意补全图形,如图所示;
(2)由旋转的性质得到∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到三角形BDC与三角形EFC全等,利用全等三角形对应角相等即可得证.
【解答】解:(1)补全图形,如图所示;
(2)由旋转的性质得:∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
在△BDC和△EFC中,
,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
23.(10分)已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
【分析】(1)根据等腰直角三角形的性质、全等三角形的判定定理证明Rt△BCD≌Rt△ACE,根据全等三角形的性质解答;
(2)证明△EBD≌△ADF,根据全等三角形的性质证明即可.
【解答】解:(1)AE=DB,AE⊥DB,
证明:∵△ABC与△DEC是等腰直角三角形,
∴AC=BC,EC=DC,
在Rt△BCD和Rt△ACE中,
,
∴Rt△BCD≌Rt△ACE,
∴AE=BD,∠AEC=∠BDC,
∵∠BCD=90°,
∴∠DHE=90°,
∴AE⊥DB;
(2)DE=AF,DE⊥AF,
证明:设DE与AF交于N,
由题意得,BE=AD,
∵∠EBD=∠C+∠BDC=90°+∠BDC,
∠ADF=∠BDF+∠BDC=90°+∠BDC,
∴∠EBD=∠ADF,
在△EBD和△ADF中,
,
∴△EBD≌△ADF,
∴DE=AF,∠E=∠FAD,
∵∠E=45°,∠EDC=45°,
∴∠FAD=45°,
∴∠AND=90°,即DE⊥AF.
图形的平移与旋转
一、选择题(每小题3分,共30分)
1.下列图形中,既是中心对称图形,又是轴对称图形的是( )
A.
B.
C.
D.
2.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
3.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(﹣2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再把△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1,则点A的对应点A2的坐标是( )
A.(5,2)
B.(1,0)
C.(3,﹣1)
D.(5,﹣2)
4.如图,∠C=90°,AC=4,BC=3,△ADE由△ABC旋转而成,则BE的长为( )
A.1
B.
C.1.2
D.2
5.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为10,则△BCE的面积为( )
A.5
B.6
C.10
D.4
6.经过下列变换,不能由图①所示的基本图形得到图②的是( )
A.旋转和平移
B.中心对称和轴对称
C.平移和轴对称
D.中心对称
7.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=3,则AE的长为( )
A.
B.5
C.8
D.4
8.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
9.将含有30°角的直角三角板OAB如图放置在平面直角坐标中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A.(,1)
B.(1,﹣)
C.(,﹣)
D.(﹣,)
10.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与
CD1交于点O,则线段AD1的长为( )
A.6
B.10
C.8
D.
二、填空题(每小题3分,共24分)
11.如果,那么
.
12.如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′的度数是
.
13.如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为
.
14.如图,Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,下列结论:
①△ABC≌△DEF;②∠DEF=90°;③AC=DF;④EC=CF;⑤S四动形ABEG=S四边形DGCF.其中正确的有
(填序号).
15.边长为1的正方形网格在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为A(3,3),B(5,0),若A1的坐标为(﹣5,﹣3),则B1的坐标为
.
16.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为
.
17.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB′C′,点B、C的对应点分别为点B'、C′,AB′与BC相交于点D,当B′C′∥AB时,则CD=
.
18.如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(,0)、B(0,4),则点B2020的横坐标为
.
三、解答题(共46分)
19.(8分)如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°得到线段AE连结CD、BE.
(1)求证:∠AEB=∠ADC;
(2)连结DE,若∠ADC=115°,求∠BED的度数.
20.(8分)如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
21.(10分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
22.(10分)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
23.(10分)已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.下列图形中,既是中心对称图形,又是轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、不是中心对称图形,不是轴对称图形,故此选项不合题意;
B、既是中心对称图形,又是轴对称图形,故此选项符合题意;
C、不是中心对称图形,是轴对称图形,故此选项不合题意;
D、是中心对称图形,不是轴对称图形,故此选项不合题意;
故选:B.
2.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
【分析】根据图形的对称性,用360°除以3计算即可得解.
【解答】解:∵360°÷3=120°,
∴旋转的角度是120°的整数倍,
∴旋转的角度至少是120°.
故选:C.
3.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(﹣2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再把△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1,则点A的对应点A2的坐标是( )
A.(5,2)
B.(1,0)
C.(3,﹣1)
D.(5,﹣2)
【分析】根据平移变换,旋转变换的性质画出图象即可解决问题;
【解答】解:如图,△A2B2C1即为所求.
观察图象可知:A2(5,2)
故选:A.
4.如图,∠C=90°,AC=4,BC=3,△ADE由△ABC旋转而成,则BE的长为( )
A.1
B.
C.1.2
D.2
【分析】根据BE=AB﹣AE,求出AB,AE即可解决问题;
【解答】解:在Rt△ABC中,∵∠C=90°,AC=4,BC=3,
∴AB==5,
由旋转不变性可知:AE=AC=4,
∴BE=AB﹣AE=5﹣4=1,
故选:A.
5.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为10,则△BCE的面积为( )
A.5
B.6
C.10
D.4
【分析】根据平移的性质得到AB=BD,BC∥DE,利用三角形面积公式得到S△BCD=S△ACD=5,然后利用DE∥BC得到S△BCE=S△BCD=5.
【解答】解:∵△ABC沿直线AB向右平移后到达△BDE的位置,
∴AB=BD,BC∥DE,
∴S△ABC=S△BCD=S△ACD=×10=5,
∵DE∥BC,
∴S△BCE=S△BCD=5.
故选:A.
6.经过下列变换,不能由图①所示的基本图形得到图②的是( )
A.旋转和平移
B.中心对称和轴对称
C.平移和轴对称
D.中心对称
【分析】根据旋转、平移、轴对称、中心对称的性质即可进行逐一判断.
【解答】解:因为经过旋转和平移能由图①所示的基本图形得到图②,所以A选项不符合题意;
因为经过中心对称和轴对称能由图①所示的基本图形得到图②,所以B选项不符合题意;
因为经过平移和轴对称能由图①所示的基本图形得到图②,所以C选项不符合题意;
因为经过中心对称不能由图①所示的基本图形得到图②,所以D选项符合题意.
故选:D.
7.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=3,则AE的长为( )
A.
B.5
C.8
D.4
【分析】利用旋转的性质得出四边形AECF的面积等于正方形ABCD的面积,进而可求出正方形的边长,再利用勾股定理得出答案.
【解答】解:∵把△ADE顺时针旋转△ABF的位置,
∴四边形AECF的面积等于正方形ABCD的面积等于25,
∴AD=DC=5,
∵DE=3,
∴Rt△ADE中,AE===.
故选:A.
8.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
【分析】根据旋转的性质和三角形内角和解答即可.
【解答】解:∵将△ABC绕点C顺时针旋转90°得到△EDC.
∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,
∴∠CAD=45°,∠ACD=90°﹣20°=70°,
∴∠ADC=180°﹣45°﹣70°=65°,
故选:C.
9.将含有30°角的直角三角板OAB如图放置在平面直角坐标中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A.(,1)
B.(1,﹣)
C.(,﹣)
D.(﹣,)
【分析】求出旋转后OA与y轴夹角为45°,然后求出点A′的横坐标与纵坐标,从而得解.
【解答】解:如图,
∵三角板绕原点O顺时针旋转75°,
∴旋转后OA与y轴夹角为45°,
∵OA=2,
∴OA′=2,
∴点A′的横坐标为2×=,
纵坐标为﹣2×=﹣,
所以,点A′的坐标为(,﹣).
故选:C.
10.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与
CD1交于点O,则线段AD1的长为( )
A.6
B.10
C.8
D.
【分析】先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°,然后判断出△ACO是等腰直角三角形,再根据等腰直角三角形的性质求出AO、CO,AB⊥CO,再求出OD1然后利用勾股定理列式计算即可得解.
【解答】解:∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°﹣30°=60°,
∴∠ACD=90°﹣60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°,
又∵∠A=45°,
∴△ACO是等腰直角三角形,
∴AO=CO=AB=×12=6,AB⊥CO,
∵DC=14,
∴D1C=DC=14,
∴D1O=14﹣6=8,
在Rt△AOD1中,AD1===10.
故选:B.
二、填空题(每小题3分,共24分)
11.如果,那么 .
【分析】观察图象的变化,根据旋转变换的性质轴对称的性质即可解决问题.
【解答】解:由题意性质180,可得图形:
12.如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′的度数是 105° .
【分析】由旋转的性质可得∠BAC=∠B'AC'=75°,AB=AB',由平行线的性质和等腰三角形的性质可得∠BAB'=30°,即可求解.
【解答】解:∵以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',
∴∠BAC=∠B'AC'=75°,AB=AB',
∵BB'∥AC',
∴∠C'AB'=∠AB'B=75°,
∵AB=AB',
∴∠AB'B=∠BB'A=75°,
∴∠BAB'=30°,
∴∠BAC'=∠BAB'+∠B'A'C'=75°+30°=105°,
故答案为:105°.
13.如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为 (6,0) .
【分析】由平移的性质和旋转的性质作出图形,即可得出答案.
【解答】解:如图所示:
∵A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,
∴A′、B′、C′的坐标分别为(4,4),B(3,1),C(2,2),
再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,
则点A″的坐标为
(6,0);
故答案为:(6,0).
14.如图,Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,下列结论:
①△ABC≌△DEF;②∠DEF=90°;③AC=DF;④EC=CF;⑤S四动形ABEG=S四边形DGCF.其中正确的有 ①②③⑤ (填序号).
【分析】由平移的性质可得Rt△ABC≌△Rt△DEF,由全等三角形的性质依次判断可求解.
【解答】解:∵Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,
∴Rt△ABC≌△Rt△DEF,故①正确;
∴S△ABC=S△DEF,∠ABC=∠DEF=90°,BC=EF,AC=DF,故②、③正确;
∴S四动形ABEG=S四边形DGCF,CF=BE,故④错误,⑤正确,
故答案为:①②③⑤.
15.边长为1的正方形网格在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为A(3,3),B(5,0),若A1的坐标为(﹣5,﹣3),则B1的坐标为 (﹣3,﹣6) .
【分析】各对应点之间的关系是横坐标加﹣8,纵坐标加﹣6,那么让点B的横坐标加﹣8,纵坐标加﹣6即为点B1的坐标.
【解答】解:由点A到A1可知:各对应点之间的关系是横坐标加﹣8,纵坐标加﹣6,那点B到B1的移动规律也如此,则B1的横坐标为5+(﹣8)=﹣3;纵坐标为0+(﹣6)=﹣6;
∴B1的坐标为(﹣3,﹣6).
故答案为:(﹣3,﹣6).
16.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 6 .
【分析】根据中心对称图形的概念,以及长方形的面积公式即可解答.
【解答】解:∵直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D,OB=3,OD=2,
∴AB=2,
∴阴影部分的面积之和为3×2=6.
故答案为:6.
17.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB′C′,点B、C的对应点分别为点B'、C′,AB′与BC相交于点D,当B′C′∥AB时,则CD= .
【分析】设CD=x,由B′C′∥AB,可推得∠BAD=∠B′,由旋转的性质得:∠B=∠B′,于是得到∠BAD=∠B,AC=AC′=4,AD=BD=8﹣x,由勾股定理可求解.
【解答】解:设CD=x,
∵B′C′∥AB,
∴∠BAD=∠B′,
由旋转的性质得:∠B=∠B′,AC=AC′=6,
∴∠BAD=∠B,
∴AD=BD=8﹣x,
∴(8﹣x)2=x2+62,
∴x=,
∴CD=,
故答案为:.
18.如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(,0)、B(0,4),则点B2020的横坐标为 10100 .
【分析】首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…,即可得每偶数之间的B相差10个单位长度,根据这个规律可以求得B2020的坐标.
【解答】解:由图象可知点B2020在第一象限,
∵OA=,OB=4,∠AOB=90°,
∴AB===,
∴B2(10,4),B4(20,4),B6(30,4),…
∴B2020(10100,4).
∴点B2020横坐标为10100.
故答案为10100
三、解答题(共46分)
19.(8分)如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°得到线段AE连结CD、BE.
(1)求证:∠AEB=∠ADC;
(2)连结DE,若∠ADC=115°,求∠BED的度数.
【分析】(1)由等边三角形的性质知∠BAC=60°,AB=AC,由旋转的性质知∠DAE=60°,AE=AD,从而得∠EAB=∠DAC,再证△EAB≌△DAC可得答案;
(2)由∠DAE=60°,AE=AD知△EAD为等边三角形,即∠AED=60°,继而由∠AEB=∠ADC=115°可得.
【解答】解:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
,
∴△EAB≌△DAC(SAS),
∴∠AEB=∠ADC;
(2)如图,
∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形.
∴∠AED=60°,
又∵∠AEB=∠ADC=115°.
∴∠BED=55°.
20.(8分)如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
【分析】由平移的性质可知△ABC平移的距离,以及BE=2BC=4,DE=AC=2,故可得出BD⊥DE,由∠E=∠ACB=60°,在Rt△BDE中利用勾股定理即可得出BD的长.
【解答】解:∵△DCE由△ABC平移而成,
∴△ABC平移的距离为:BC=2,
且BE=2BC=4,DE=AC=2,∠E=∠ACB=60°,
∴DE=BE,
∴BD⊥DE,
又∵∠E=∠ACB=60°,
∴AC∥DE,
∴BD⊥AC,
∴△BED是直角三角形,
∵BE=4,DE=2,
∴BD==2.
21.(10分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
【分析】(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
【解答】解:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
22.(10分)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【分析】(1)根据题意补全图形,如图所示;
(2)由旋转的性质得到∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到三角形BDC与三角形EFC全等,利用全等三角形对应角相等即可得证.
【解答】解:(1)补全图形,如图所示;
(2)由旋转的性质得:∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
在△BDC和△EFC中,
,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
23.(10分)已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
【分析】(1)根据等腰直角三角形的性质、全等三角形的判定定理证明Rt△BCD≌Rt△ACE,根据全等三角形的性质解答;
(2)证明△EBD≌△ADF,根据全等三角形的性质证明即可.
【解答】解:(1)AE=DB,AE⊥DB,
证明:∵△ABC与△DEC是等腰直角三角形,
∴AC=BC,EC=DC,
在Rt△BCD和Rt△ACE中,
,
∴Rt△BCD≌Rt△ACE,
∴AE=BD,∠AEC=∠BDC,
∵∠BCD=90°,
∴∠DHE=90°,
∴AE⊥DB;
(2)DE=AF,DE⊥AF,
证明:设DE与AF交于N,
由题意得,BE=AD,
∵∠EBD=∠C+∠BDC=90°+∠BDC,
∠ADF=∠BDF+∠BDC=90°+∠BDC,
∴∠EBD=∠ADF,
在△EBD和△ADF中,
,
∴△EBD≌△ADF,
∴DE=AF,∠E=∠FAD,
∵∠E=45°,∠EDC=45°,
∴∠FAD=45°,
∴∠AND=90°,即DE⊥AF.
