_苏科版八年级上册数学第3章3.1~3.2勾股定理及逆定理阶段培优训练试卷(word解析版)
文档属性
| 名称 | _苏科版八年级上册数学第3章3.1~3.2勾股定理及逆定理阶段培优训练试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 887.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览



文档简介
2020-2021学年苏科版八年级上学期数学第3章勾股定理3.1~3.2阶段培优训练试卷(1)
一、选择题
1、下列说法正确的是(
).
A.若、、是的三边长,则
B.若、、是的三边长,则
C.若、、是的三边长,,则
D.若、、是的三边长,,则
2、如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次
为2,4,3,则正方形D的面积为( )
A.9
B.8
C.27
D.45
3、如图,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,且ED⊥AB,若AC=6,BC=8,则BD的长( )
A.2
B.3
C.4
D.5
4、如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A.1.5
B.2.4
C.2.5
D.3.5
5、如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要(??
)
A.?4米???????????????????????????????????????B.?5米???????????????????????????????????????C.?6米???????????????????????????????????????D.?7米
6、2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )
A.2
B.0.5
C.13
D.1
7、a、b、c为△ABC三边,下列条件不能判断它是直角三角形的是( )
A.a2=c2﹣b2
B.∠A:∠B:∠C=3:4:5
C.a=3,b=4,c=5
D.a=5k,b=12k,c=13k(k为正整数)
8、适合下列条件的△ABC中,
直角三角形的个数为
①
②,∠A=45°;
③∠A=32°,
∠B=58°;
④
⑤
⑥
⑦
⑧
A.2个
B.3个
C.4个
D.5个
9、下列各组线段中的三个长度①9、12、15;②7、24、25;③32、42、52;④5,12,13,其中可以构成直角三角形的有( )
A.1组
B.2组
C.3组
D.4组
10、如图,方格中的点A、B、C、D、E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是(
)
A.2和3
B.3和3
C.2和4
D.3和4
二、填空题
11、在△ABC中,∠C=90°,BC=12,AB=13,AC=
.
12、如图,在△ABC中,∠BAC=90°,AC=16,BC=20,AD⊥BC,垂足为D,则AD的长为
.
13、把图1中长和宽分别6和4的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2的正方形,则图2中小正方形ABCD的面积为 .
14、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大正方形M的边长是3,则正方形A、B、C、D、E、F的面积之和是
.
15、若直角三角形的两边长分别为a,b,且满足a2﹣6a+9+|b﹣4|=0,则该直角三角形的第三边长的平方为
.
16、如图,有一个三级台阶,它的每一级的长,
宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,
则蚂蚁沿着台阶表面爬到点的最短路程是____
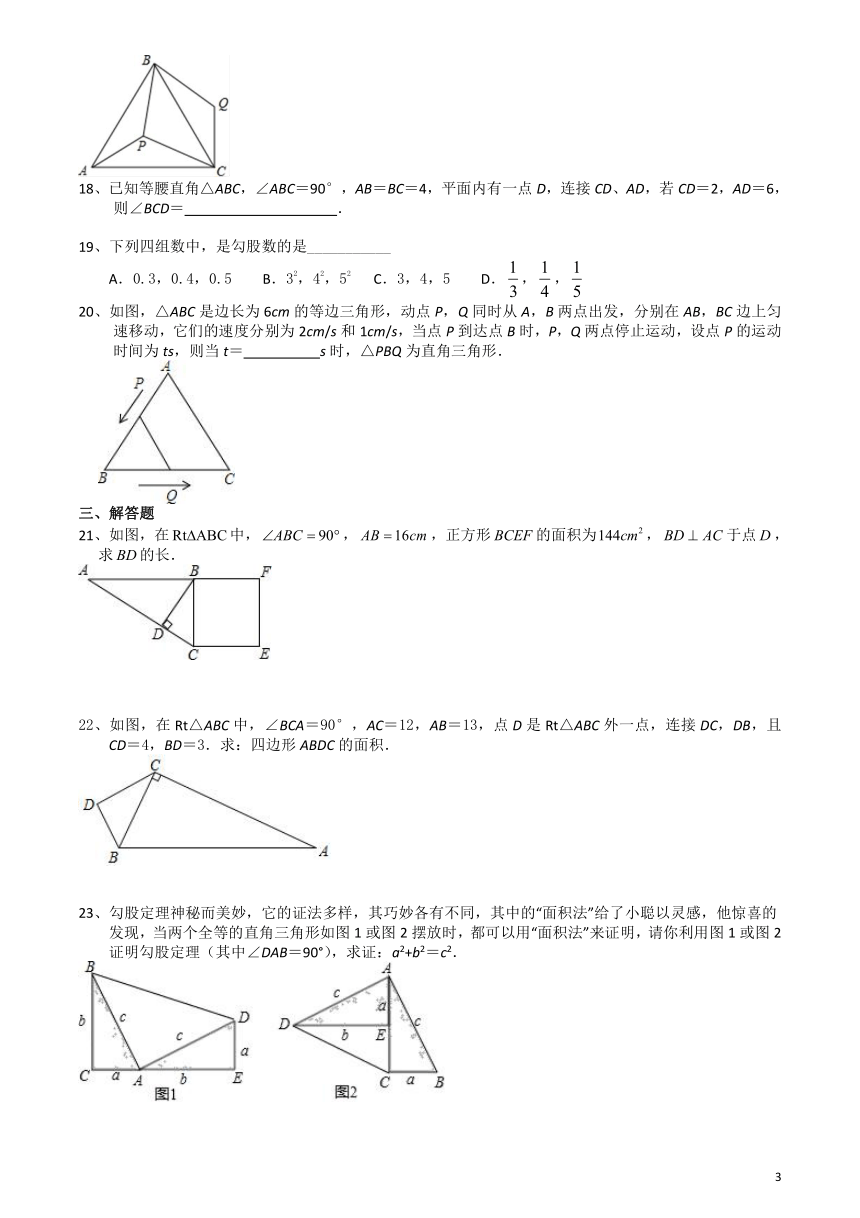
17、如图,点P是等边三角形ABC内一点,且PA=3,PB=4,
PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.
18、已知等腰直角△ABC,∠ABC=90°,AB=BC=4,平面内有一点D,连接CD、AD,若CD=2,AD=6,则∠BCD=
.
19、下列四组数中,是勾股数的是___________
A.0.3,0.4,0.5
B.32,42,52
C.3,4,5
D.,,
20、如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t=
s时,△PBQ为直角三角形.
三、解答题
21、如图,在中,,,正方形的面积为,于点,求的长.
22、如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.求:四边形ABDC的面积.
23、勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,请你利用图1或图2证明勾股定理(其中∠DAB=90°),求证:a2+b2=c2.
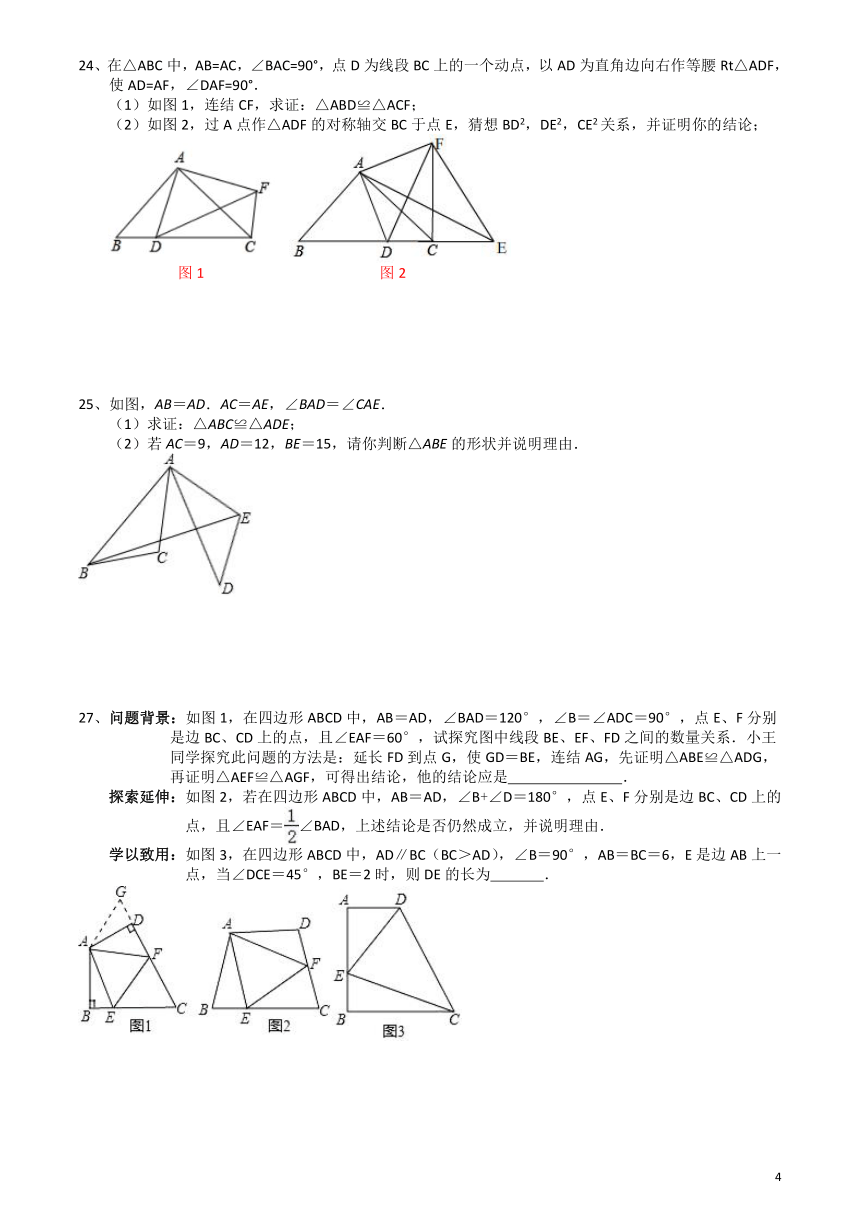
24、在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上的一个动点,以AD为直角边向右作等腰Rt△ADF,使AD=AF,∠DAF=90°.
(1)如图1,连结CF,求证:△ABD≌△ACF;
(2)如图2,过A点作△ADF的对称轴交BC于点E,猜想BD2,DE2,CE2关系,并证明你的结论;
图1
图2
25、如图,AB=AD.AC=AE,∠BAD=∠CAE.
(1)求证:△ABC≌△ADE;
(2)若AC=9,AD=12,BE=15,请你判断△ABE的形状并说明理由.
27、问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E、F分别是边BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使GD=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是
.
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别是边BC、CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.
学以致用:如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是边AB上一点,当∠DCE=45°,BE=2时,则DE的长为
.
2020-2021学年苏科版八年级上学期数学第3章勾股定理3.1~3.2阶段培优训练试卷(1)
(答案)
一、选择题
1、下列说法正确的是(
).
A.若、、是的三边长,则
B.若、、是的三边长,则
C.若、、是的三边长,,则
D.若、、是的三边长,,则
解:由勾股定理,
A、没有确定直角和斜边,故A
错误;
B、没有确定斜边,故B错误;
C、斜边为,则,故C错误;
D、,则与为直角边,为斜边,则,故D正确;
故选择:D.
2、如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次
为2,4,3,则正方形D的面积为( )
A.9
B.8
C.27
D.45
【解答】∵正方形A.
B.?C的面积依次为2、4、3
∴根据图形得:2+4=x?3
解得:x=9
故选A.
3、如图,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,且ED⊥AB,若AC=6,BC=8,则BD的长( )
A.2
B.3
C.4
D.5
【解析】∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB,AB=10
∵AE为△ABC的角平分线,ED⊥AB,
∴CE=ED,
∴△ACE≌△ADE(AAS),
∴AD=AC=6,
∴BD=10﹣6=4,
故选:C.
4、如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A.1.5
B.2.4
C.2.5
D.3.5
【解答】连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得,
又S△AMCMN?ACAM?MC,
∴MN2.4.
故选B.
5、如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要(??
)
A.?4米???????????????????????????????????????B.?5米???????????????????????????????????????C.?6米???????????????????????????????????????D.?7米
【答案】解:在Rt△ABC中,AC=
=4米,
故可得地毯长度=AC+BC=7米,
故答案为:D
6、2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )
A.2
B.0.5
C.13
D.1
【解答】∵(a+b)2=49,
∴a2+2ab+b2=49,
∵大正方形的面积为25,
∴2ab=49﹣25=24,
∴小正方形的面积为25﹣24=1.
故选:D.
7、a、b、c为△ABC三边,下列条件不能判断它是直角三角形的是( )
A.a2=c2﹣b2
B.∠A:∠B:∠C=3:4:5
C.a=3,b=4,c=5
D.a=5k,b=12k,c=13k(k为正整数)
【解答】A.若a2=c2﹣b2,则△ABC为直角三角形,故本选项不合题意;
B.若∠A:∠B:∠C=3:4:5,则最大角∠C<90°,△ABC不是直角三角形,故本选项符合题意;
C.若a=3,b=4,c=5,则△ABC为直角三角形,故本选项不合题意;
D.若a=5k,b=12k,c=13k(k为正整数),则a2+b2=c2,那么这个三角形就是直角三角形,故本选项不合题意.
故选:B.
8、适合下列条件的△ABC中,
直角三角形的个数为
①
②,∠A=45°;
③∠A=32°,
∠B=58°;
④
⑤
⑥
⑦
⑧
A.2个
B.3个
C.4个
D.5个
【答案】根据勾股定理的逆定理,可分别求出各边的平方,然后计算判断:,故①不能构成直角三角形;
当a=6,∠A=45°时,②不足以判定该三角形是直角三角形;
根据直角三角形的两锐角互余,可由∠A+∠B=90°,可知③是直角三角形;
根据72=49,242=576,252=625,可知72+242=252,故④能够成直角三角形;
由三角形的三边关系,2+2=4可知⑤不能构成三角形;
令a=3x,b=4x,c=5x,可知a2+b2=c2,故⑥能够成直角三角形;
根据三角形的内角和可知⑦不等构成直角三角形;
由a2=25,b2=144,c2=169,可知a2+b2=c2,故⑧能够成直角三角形.故选:C.
9、下列各组线段中的三个长度①9、12、15;②7、24、25;③32、42、52;④5,12,13,其中可以构成直角三角形的有( )
A.1组
B.2组
C.3组
D.4组
【解答】①中有92+122=152;
②中有72+242=252;
③中(32)2+(42)25≠(52)2;
④中52+122=132;
所以可以构成3组直角三角形.
故选C.
10、如图,方格中的点A、B、C、D、E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是(
)
A.2和3
B.3和3
C.2和4
D.3和4
【解答】解:(1)如图,为等腰三角形有两种
由勾股定理易知:ED=DC=,
符合题意,
由勾股定理易知:AE=EC=,符合题意,
(2)如图,为直角三角形有三种
由勾股定理及格点图知:AB=2,BE=4,AE=,
满足,由勾股定理逆定理知?ABE为直角三角形;
由勾股定理及格点图知:BC=2,BE=4,CE=,
满足,由勾股定理逆定理知?CBE为直角三角形;由勾股定理及格点图知:DC=,DE=,CE=,
满足,由勾股定理逆定理知?CDE为直角三角形,故选:A
二、填空题
11、在△ABC中,∠C=90°,BC=12,AB=13,AC= 5 .
【解答】∵在△ABC中,∠C=90°,BC=12,AB=13,
∴AC5.AC=5
故答案为:5.
12、如图,在△ABC中,∠BAC=90°,AC=16,BC=20,AD⊥BC,垂足为D,则AD的长为 .
【解答】∵∠BAC=90°,AC=16,BC=20,
∴AB144,AB=12
∵S△ABCAB?ACBC?AD,
∴12×1620AD,
∴AD.
故答案为:.
13、把图1中长和宽分别6和4的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2的正方形,则图2中小正方形ABCD的面积为 .
【解答】6﹣4=2,
2×2=4.
故图2中小正方形ABCD的面积为4.
故答案为4.
14、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大正方形M的边长是3,则正方形A、B、C、D、E、F的面积之和是
.
【解答】根据勾股定理得到:A与B的面积的和是E的面积;C与D的面积的和是F的面积;而E,F的面积的和是M的面积.
即A、B、C、D、E、F的面积之和为2个M的面积.
∵M的面积是32=9,
∴A、B、C、D、E、F的面积之和为9×2=18.
故答案为18.
15、若直角三角形的两边长分别为a,b,且满足a2﹣6a+9+|b﹣4|=0,则该直角三角形的第三边长的平方为 7或25 .
【解答】∵a2﹣6a+9+|b﹣4|=0,
∴(a﹣3)2,b﹣4=0,
∴a=3,b=4,
∴直角三角形的第三边长5,或直角三角形的第三边长
∴直角三角形的第三平方为25或7,
故答案为:7或25.
16、如图,有一个三级台阶,它的每一级的长,
宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,
则蚂蚁沿着台阶表面爬到点的最短路程是____
【解答】解:三级台阶平面展开图为长方形,长为16,宽为(3+1)×3,
则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到B点最短路程为x,
由勾股定理得:x2=162+[(3+1)×3]2=400,解得x=20.
17、如图,点P是等边三角形ABC内一点,且PA=3,PB=4,
PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.
【解答】解:连接PQ,
由题意可知△ABP≌△CBQ
则QB=PB=4,PA=QC=3,∠ABP=∠CBQ,
∵△ABC是等边三角形,∴∠ABC=∠ABP+∠PBC=60°,
∴∠PBQ=∠CBQ+∠PBC=60°,∴△BPQ为等边三角形,∴PQ=PB=BQ=4,
又∵PQ=4,PC=5,QC=3,∴PQ2+QC2=PC2,∴∠PQC=90°,
∵△BPQ为等边三角形,∴∠BQP=60°,
∴∠BQC=∠BQP+∠PQC=150°∴∠APB=∠BQC=150°
18、已知等腰直角△ABC,∠ABC=90°,AB=BC=4,平面内有一点D,连接CD、AD,若CD=2,AD=6,则∠BCD=
.
【解答】∵∠ABC=90°,AB=BC=4,
∴AC2=42+42=32,而CD2=4,AD2=62=36,
∴AD2=AC2+CD2,
∴△ACD为直角三角形,∠ACD=90°;
∵△ABC为等腰直角三角形,
∴∠ACB=45°,
∴①∠BCD=90°+45°=135°;
②∠BCD=90°﹣45°=45°.
故∠BCD=135°或45°.
故答案为:135°或45°.
19、下列四组数中,是勾股数的是___________
A.0.3,0.4,0.5
B.32,42,52
C.3,4,5
D.
【解答】A、0.32+0.42=0.52,能构成直角三角形,但不是整数,不是勾股数,故本选项不符合题意;
B、(32)2+(42)2≠(52)2,不是勾股数,故本选项不符合题意;
C、32+42=52,是勾股数,故本选项符合题意;
D、()2+()2≠()2,不是勾股数,故本选项不符合题意.
故选C.
20、如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t= 或 s时,△PBQ为直角三角形.
【解答】∵△ABC是等边三角形,
∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=6﹣2x,BQ=x,
∴6﹣2x=2x,
解得x;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴x=2(6﹣2x),
解得x.
答:或秒时,△BPQ是直角三角形.
故答案为或.
三、解答题
21、如图,在中,,,正方形的面积为,于点,求的长.
【解答】解:正方形的面积为,
,
,,
.
,
,
.
22、如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.求:四边形ABDC的面积.
【解答】∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴;
∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=BC2,∴△BCD是直角三角形,
∴四边形ABDC的面积=S△ABC+S△BCD12×53×4=36.
23、勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,请你利用图1或图2证明勾股定理(其中∠DAB=90°),求证:a2+b2=c2.
【解答】利用图1进行证明:
证明:∵∠DAB=90°,点C,A,E在一条直线上,BC∥DE,则CE=a+b,
∵S四边形BCED=S△ABC+S△ABD+S△AED=ab+c2+ab,
又∵S四边形BCED=(a+b)2,∴ab+c2+ab=(a+b)2,∴a2+b2=c2.
利用图2进行证明:
证明:如图,连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a),∴b2+ab=c2+a(b﹣a),∴a2+b2=c2.
24、在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上的一个动点,以AD为直角边向右作等腰Rt△ADF,使AD=AF,∠DAF=90°.
(1)如图1,连结CF,求证:△ABD≌△ACF;
(2)如图2,过A点作△ADF的对称轴交BC于点E,猜想BD2,DE2,CE2关系,并证明你的结论;
图1
图2
【解答】(1)∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,
在△ABD和△ACF中,,∴△ABD≌△ACF;
(2)CE2+BD2=DE2;理由:∵AB=AC,∠BAC=90°,∴∠ABD=∠ACB=45°,
由(1)知,△ABD≌△ACF,∴BD=CF,∠ACF=∠ABD=45°,∴∠ECF=90°,
根据勾股定理得,CE2+CF2=EF2,
∵AE是△ADF的对称轴,∴DE=EF,∴CE2+BD2=DE2;
25、如图,AB=AD.AC=AE,∠BAD=∠CAE.
(1)求证:△ABC≌△ADE;
(2)若AC=9,AD=12,BE=15,请你判断△ABE的形状并说明理由.
【解答】(1)证明:∵∠BAD=∠CAE,∴∠BAC=∠DAE,
在△ABC和△ADE中,,∴△ABC≌△ADE(SAS).
(2)解:结论△ABE是直角三角形.
理由:∵AB=AD=12,AE=AC=9,BE=15,
∴AB2+AE2=122+92=225,BE2=225,
∴AB2+AE2=BE2,∴∠BAE=90°,∴△BAE是直角三角形.
26、在△ABC中,D为BC的中点,AB=5,AD=6,AC=13.试判断AD与AB的位置关系.
【解答】
延长AD至E,使得,连接BE,
∵D为BC的中点,∴,
在△ADC和△EDB中,,∴△ADC≌△EDB(SAS),∴,
∵,∴,
∵,∴,∴,∴AD⊥AB.
27、问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E、F分别是边BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使GD=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是
.
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别是边BC、CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.
学以致用:如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是边AB上一点,当∠DCE=45°,BE=2时,则DE的长为
.
【解答】
问题背景:解:如图1,在△ABE和△ADG中,
∵,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,∵,∴△AEF≌△AGF(SAS),∴EF=FG,
∵FG=DG+DF=BE+FD,∴EF=BE+FD;故答案为:EF=BE+FD.
探索延伸:解:结论EF=BE+DF仍然成立;理由:如图2,延长FD到点G.使DG=BE.连结AG,
在△ABE和△ADG中,∵,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,∵,∴△AEF≌△AGF(SAS),∴EF=FG,
∵FG=DG+DF=BE+FD,∴EF=BE+FD;
学以致用:如图3,过点C作CG⊥AD,交AD的延长线于点G,
由【探索延伸】和题设知:DE=DG+BE,设DG=x,则AD=6﹣x,DE=x+3,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴(6﹣x)2+32=(x+3)2,解得x=2.∴DE=2+3=5.故答案是:5.
一、选择题
1、下列说法正确的是(
).
A.若、、是的三边长,则
B.若、、是的三边长,则
C.若、、是的三边长,,则
D.若、、是的三边长,,则
2、如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次
为2,4,3,则正方形D的面积为( )
A.9
B.8
C.27
D.45
3、如图,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,且ED⊥AB,若AC=6,BC=8,则BD的长( )
A.2
B.3
C.4
D.5
4、如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A.1.5
B.2.4
C.2.5
D.3.5
5、如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要(??
)
A.?4米???????????????????????????????????????B.?5米???????????????????????????????????????C.?6米???????????????????????????????????????D.?7米
6、2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )
A.2
B.0.5
C.13
D.1
7、a、b、c为△ABC三边,下列条件不能判断它是直角三角形的是( )
A.a2=c2﹣b2
B.∠A:∠B:∠C=3:4:5
C.a=3,b=4,c=5
D.a=5k,b=12k,c=13k(k为正整数)
8、适合下列条件的△ABC中,
直角三角形的个数为
①
②,∠A=45°;
③∠A=32°,
∠B=58°;
④
⑤
⑥
⑦
⑧
A.2个
B.3个
C.4个
D.5个
9、下列各组线段中的三个长度①9、12、15;②7、24、25;③32、42、52;④5,12,13,其中可以构成直角三角形的有( )
A.1组
B.2组
C.3组
D.4组
10、如图,方格中的点A、B、C、D、E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是(
)
A.2和3
B.3和3
C.2和4
D.3和4
二、填空题
11、在△ABC中,∠C=90°,BC=12,AB=13,AC=
.
12、如图,在△ABC中,∠BAC=90°,AC=16,BC=20,AD⊥BC,垂足为D,则AD的长为
.
13、把图1中长和宽分别6和4的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2的正方形,则图2中小正方形ABCD的面积为 .
14、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大正方形M的边长是3,则正方形A、B、C、D、E、F的面积之和是
.
15、若直角三角形的两边长分别为a,b,且满足a2﹣6a+9+|b﹣4|=0,则该直角三角形的第三边长的平方为
.
16、如图,有一个三级台阶,它的每一级的长,
宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,
则蚂蚁沿着台阶表面爬到点的最短路程是____
17、如图,点P是等边三角形ABC内一点,且PA=3,PB=4,
PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.
18、已知等腰直角△ABC,∠ABC=90°,AB=BC=4,平面内有一点D,连接CD、AD,若CD=2,AD=6,则∠BCD=
.
19、下列四组数中,是勾股数的是___________
A.0.3,0.4,0.5
B.32,42,52
C.3,4,5
D.,,
20、如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t=
s时,△PBQ为直角三角形.
三、解答题
21、如图,在中,,,正方形的面积为,于点,求的长.
22、如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.求:四边形ABDC的面积.
23、勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,请你利用图1或图2证明勾股定理(其中∠DAB=90°),求证:a2+b2=c2.
24、在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上的一个动点,以AD为直角边向右作等腰Rt△ADF,使AD=AF,∠DAF=90°.
(1)如图1,连结CF,求证:△ABD≌△ACF;
(2)如图2,过A点作△ADF的对称轴交BC于点E,猜想BD2,DE2,CE2关系,并证明你的结论;
图1
图2
25、如图,AB=AD.AC=AE,∠BAD=∠CAE.
(1)求证:△ABC≌△ADE;
(2)若AC=9,AD=12,BE=15,请你判断△ABE的形状并说明理由.
27、问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E、F分别是边BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使GD=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是
.
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别是边BC、CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.
学以致用:如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是边AB上一点,当∠DCE=45°,BE=2时,则DE的长为
.
2020-2021学年苏科版八年级上学期数学第3章勾股定理3.1~3.2阶段培优训练试卷(1)
(答案)
一、选择题
1、下列说法正确的是(
).
A.若、、是的三边长,则
B.若、、是的三边长,则
C.若、、是的三边长,,则
D.若、、是的三边长,,则
解:由勾股定理,
A、没有确定直角和斜边,故A
错误;
B、没有确定斜边,故B错误;
C、斜边为,则,故C错误;
D、,则与为直角边,为斜边,则,故D正确;
故选择:D.
2、如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次
为2,4,3,则正方形D的面积为( )
A.9
B.8
C.27
D.45
【解答】∵正方形A.
B.?C的面积依次为2、4、3
∴根据图形得:2+4=x?3
解得:x=9
故选A.
3、如图,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,且ED⊥AB,若AC=6,BC=8,则BD的长( )
A.2
B.3
C.4
D.5
【解析】∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB,AB=10
∵AE为△ABC的角平分线,ED⊥AB,
∴CE=ED,
∴△ACE≌△ADE(AAS),
∴AD=AC=6,
∴BD=10﹣6=4,
故选:C.
4、如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A.1.5
B.2.4
C.2.5
D.3.5
【解答】连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得,
又S△AMCMN?ACAM?MC,
∴MN2.4.
故选B.
5、如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要(??
)
A.?4米???????????????????????????????????????B.?5米???????????????????????????????????????C.?6米???????????????????????????????????????D.?7米
【答案】解:在Rt△ABC中,AC=
=4米,
故可得地毯长度=AC+BC=7米,
故答案为:D
6、2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )
A.2
B.0.5
C.13
D.1
【解答】∵(a+b)2=49,
∴a2+2ab+b2=49,
∵大正方形的面积为25,
∴2ab=49﹣25=24,
∴小正方形的面积为25﹣24=1.
故选:D.
7、a、b、c为△ABC三边,下列条件不能判断它是直角三角形的是( )
A.a2=c2﹣b2
B.∠A:∠B:∠C=3:4:5
C.a=3,b=4,c=5
D.a=5k,b=12k,c=13k(k为正整数)
【解答】A.若a2=c2﹣b2,则△ABC为直角三角形,故本选项不合题意;
B.若∠A:∠B:∠C=3:4:5,则最大角∠C<90°,△ABC不是直角三角形,故本选项符合题意;
C.若a=3,b=4,c=5,则△ABC为直角三角形,故本选项不合题意;
D.若a=5k,b=12k,c=13k(k为正整数),则a2+b2=c2,那么这个三角形就是直角三角形,故本选项不合题意.
故选:B.
8、适合下列条件的△ABC中,
直角三角形的个数为
①
②,∠A=45°;
③∠A=32°,
∠B=58°;
④
⑤
⑥
⑦
⑧
A.2个
B.3个
C.4个
D.5个
【答案】根据勾股定理的逆定理,可分别求出各边的平方,然后计算判断:,故①不能构成直角三角形;
当a=6,∠A=45°时,②不足以判定该三角形是直角三角形;
根据直角三角形的两锐角互余,可由∠A+∠B=90°,可知③是直角三角形;
根据72=49,242=576,252=625,可知72+242=252,故④能够成直角三角形;
由三角形的三边关系,2+2=4可知⑤不能构成三角形;
令a=3x,b=4x,c=5x,可知a2+b2=c2,故⑥能够成直角三角形;
根据三角形的内角和可知⑦不等构成直角三角形;
由a2=25,b2=144,c2=169,可知a2+b2=c2,故⑧能够成直角三角形.故选:C.
9、下列各组线段中的三个长度①9、12、15;②7、24、25;③32、42、52;④5,12,13,其中可以构成直角三角形的有( )
A.1组
B.2组
C.3组
D.4组
【解答】①中有92+122=152;
②中有72+242=252;
③中(32)2+(42)25≠(52)2;
④中52+122=132;
所以可以构成3组直角三角形.
故选C.
10、如图,方格中的点A、B、C、D、E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是(
)
A.2和3
B.3和3
C.2和4
D.3和4
【解答】解:(1)如图,为等腰三角形有两种
由勾股定理易知:ED=DC=,
符合题意,
由勾股定理易知:AE=EC=,符合题意,
(2)如图,为直角三角形有三种
由勾股定理及格点图知:AB=2,BE=4,AE=,
满足,由勾股定理逆定理知?ABE为直角三角形;
由勾股定理及格点图知:BC=2,BE=4,CE=,
满足,由勾股定理逆定理知?CBE为直角三角形;由勾股定理及格点图知:DC=,DE=,CE=,
满足,由勾股定理逆定理知?CDE为直角三角形,故选:A
二、填空题
11、在△ABC中,∠C=90°,BC=12,AB=13,AC= 5 .
【解答】∵在△ABC中,∠C=90°,BC=12,AB=13,
∴AC5.AC=5
故答案为:5.
12、如图,在△ABC中,∠BAC=90°,AC=16,BC=20,AD⊥BC,垂足为D,则AD的长为 .
【解答】∵∠BAC=90°,AC=16,BC=20,
∴AB144,AB=12
∵S△ABCAB?ACBC?AD,
∴12×1620AD,
∴AD.
故答案为:.
13、把图1中长和宽分别6和4的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2的正方形,则图2中小正方形ABCD的面积为 .
【解答】6﹣4=2,
2×2=4.
故图2中小正方形ABCD的面积为4.
故答案为4.
14、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大正方形M的边长是3,则正方形A、B、C、D、E、F的面积之和是
.
【解答】根据勾股定理得到:A与B的面积的和是E的面积;C与D的面积的和是F的面积;而E,F的面积的和是M的面积.
即A、B、C、D、E、F的面积之和为2个M的面积.
∵M的面积是32=9,
∴A、B、C、D、E、F的面积之和为9×2=18.
故答案为18.
15、若直角三角形的两边长分别为a,b,且满足a2﹣6a+9+|b﹣4|=0,则该直角三角形的第三边长的平方为 7或25 .
【解答】∵a2﹣6a+9+|b﹣4|=0,
∴(a﹣3)2,b﹣4=0,
∴a=3,b=4,
∴直角三角形的第三边长5,或直角三角形的第三边长
∴直角三角形的第三平方为25或7,
故答案为:7或25.
16、如图,有一个三级台阶,它的每一级的长,
宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,
则蚂蚁沿着台阶表面爬到点的最短路程是____
【解答】解:三级台阶平面展开图为长方形,长为16,宽为(3+1)×3,
则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到B点最短路程为x,
由勾股定理得:x2=162+[(3+1)×3]2=400,解得x=20.
17、如图,点P是等边三角形ABC内一点,且PA=3,PB=4,
PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.
【解答】解:连接PQ,
由题意可知△ABP≌△CBQ
则QB=PB=4,PA=QC=3,∠ABP=∠CBQ,
∵△ABC是等边三角形,∴∠ABC=∠ABP+∠PBC=60°,
∴∠PBQ=∠CBQ+∠PBC=60°,∴△BPQ为等边三角形,∴PQ=PB=BQ=4,
又∵PQ=4,PC=5,QC=3,∴PQ2+QC2=PC2,∴∠PQC=90°,
∵△BPQ为等边三角形,∴∠BQP=60°,
∴∠BQC=∠BQP+∠PQC=150°∴∠APB=∠BQC=150°
18、已知等腰直角△ABC,∠ABC=90°,AB=BC=4,平面内有一点D,连接CD、AD,若CD=2,AD=6,则∠BCD=
.
【解答】∵∠ABC=90°,AB=BC=4,
∴AC2=42+42=32,而CD2=4,AD2=62=36,
∴AD2=AC2+CD2,
∴△ACD为直角三角形,∠ACD=90°;
∵△ABC为等腰直角三角形,
∴∠ACB=45°,
∴①∠BCD=90°+45°=135°;
②∠BCD=90°﹣45°=45°.
故∠BCD=135°或45°.
故答案为:135°或45°.
19、下列四组数中,是勾股数的是___________
A.0.3,0.4,0.5
B.32,42,52
C.3,4,5
D.
【解答】A、0.32+0.42=0.52,能构成直角三角形,但不是整数,不是勾股数,故本选项不符合题意;
B、(32)2+(42)2≠(52)2,不是勾股数,故本选项不符合题意;
C、32+42=52,是勾股数,故本选项符合题意;
D、()2+()2≠()2,不是勾股数,故本选项不符合题意.
故选C.
20、如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t= 或 s时,△PBQ为直角三角形.
【解答】∵△ABC是等边三角形,
∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=6﹣2x,BQ=x,
∴6﹣2x=2x,
解得x;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴x=2(6﹣2x),
解得x.
答:或秒时,△BPQ是直角三角形.
故答案为或.
三、解答题
21、如图,在中,,,正方形的面积为,于点,求的长.
【解答】解:正方形的面积为,
,
,,
.
,
,
.
22、如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.求:四边形ABDC的面积.
【解答】∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴;
∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=BC2,∴△BCD是直角三角形,
∴四边形ABDC的面积=S△ABC+S△BCD12×53×4=36.
23、勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,请你利用图1或图2证明勾股定理(其中∠DAB=90°),求证:a2+b2=c2.
【解答】利用图1进行证明:
证明:∵∠DAB=90°,点C,A,E在一条直线上,BC∥DE,则CE=a+b,
∵S四边形BCED=S△ABC+S△ABD+S△AED=ab+c2+ab,
又∵S四边形BCED=(a+b)2,∴ab+c2+ab=(a+b)2,∴a2+b2=c2.
利用图2进行证明:
证明:如图,连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a),∴b2+ab=c2+a(b﹣a),∴a2+b2=c2.
24、在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上的一个动点,以AD为直角边向右作等腰Rt△ADF,使AD=AF,∠DAF=90°.
(1)如图1,连结CF,求证:△ABD≌△ACF;
(2)如图2,过A点作△ADF的对称轴交BC于点E,猜想BD2,DE2,CE2关系,并证明你的结论;
图1
图2
【解答】(1)∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,
在△ABD和△ACF中,,∴△ABD≌△ACF;
(2)CE2+BD2=DE2;理由:∵AB=AC,∠BAC=90°,∴∠ABD=∠ACB=45°,
由(1)知,△ABD≌△ACF,∴BD=CF,∠ACF=∠ABD=45°,∴∠ECF=90°,
根据勾股定理得,CE2+CF2=EF2,
∵AE是△ADF的对称轴,∴DE=EF,∴CE2+BD2=DE2;
25、如图,AB=AD.AC=AE,∠BAD=∠CAE.
(1)求证:△ABC≌△ADE;
(2)若AC=9,AD=12,BE=15,请你判断△ABE的形状并说明理由.
【解答】(1)证明:∵∠BAD=∠CAE,∴∠BAC=∠DAE,
在△ABC和△ADE中,,∴△ABC≌△ADE(SAS).
(2)解:结论△ABE是直角三角形.
理由:∵AB=AD=12,AE=AC=9,BE=15,
∴AB2+AE2=122+92=225,BE2=225,
∴AB2+AE2=BE2,∴∠BAE=90°,∴△BAE是直角三角形.
26、在△ABC中,D为BC的中点,AB=5,AD=6,AC=13.试判断AD与AB的位置关系.
【解答】
延长AD至E,使得,连接BE,
∵D为BC的中点,∴,
在△ADC和△EDB中,,∴△ADC≌△EDB(SAS),∴,
∵,∴,
∵,∴,∴,∴AD⊥AB.
27、问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E、F分别是边BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使GD=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是
.
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别是边BC、CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.
学以致用:如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是边AB上一点,当∠DCE=45°,BE=2时,则DE的长为
.
【解答】
问题背景:解:如图1,在△ABE和△ADG中,
∵,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,∵,∴△AEF≌△AGF(SAS),∴EF=FG,
∵FG=DG+DF=BE+FD,∴EF=BE+FD;故答案为:EF=BE+FD.
探索延伸:解:结论EF=BE+DF仍然成立;理由:如图2,延长FD到点G.使DG=BE.连结AG,
在△ABE和△ADG中,∵,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,∵,∴△AEF≌△AGF(SAS),∴EF=FG,
∵FG=DG+DF=BE+FD,∴EF=BE+FD;
学以致用:如图3,过点C作CG⊥AD,交AD的延长线于点G,
由【探索延伸】和题设知:DE=DG+BE,设DG=x,则AD=6﹣x,DE=x+3,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴(6﹣x)2+32=(x+3)2,解得x=2.∴DE=2+3=5.故答案是:5.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
