鲁教版(五四制)七年级上册第一章《三角形》单元综合练习—基础巩固训练(word版含答案)
文档属性
| 名称 | 鲁教版(五四制)七年级上册第一章《三角形》单元综合练习—基础巩固训练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 23:42:20 | ||
图片预览



文档简介
第一章
三角形
【基础巩固训练】
题型发散
1.选择题,把正确答案的代号填入题中括号内.
(1)下列各条件中,不能作出惟一三角形的是(
)
(A)已知两角和夹边
(B)已知两边和夹角
(C)已知两边和其中一边的对角
(D)已知三边
(2)已知一个三角形的周长为15cm,且其中两边都等于第三边的2倍,那么这个三角形的最短边为(
)
(A)1cm
(B)2cm
(C)3cm
(D)4cm
(3)如果角形的一个内角等于其余两个内角的和,那么这个三角形是
(A)锐角三角形
(B)直角三角形
(C)钝角三角形
(D)锐角三角形或钝角三角形
(4)已知线段AB,用规尺作AB的垂直平分线CD,垂足为E,在CD上取—点F,使EF=AB,连结AF,BF,那么∠AFB的度数是(
)
(A)
(B)
(C)
(D)
(5)在Rt△ABC中,∠ACB=,CD⊥AB,E为AB的中点,AC=3cm,AB=6cm,那么∠DCE的度数是(
)
(A)
(B)
(C)
(D)
2.填空题.
(1)若两个三角形全等,则它们对应高、对应中线、对应的角平分线分别______________.
(2)在△ABC中,∠B=2∠C,AD⊥AC,交BC于D,若AB=a,则CD=______________.
(3)在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大,则这个三角形是__________角三角形.
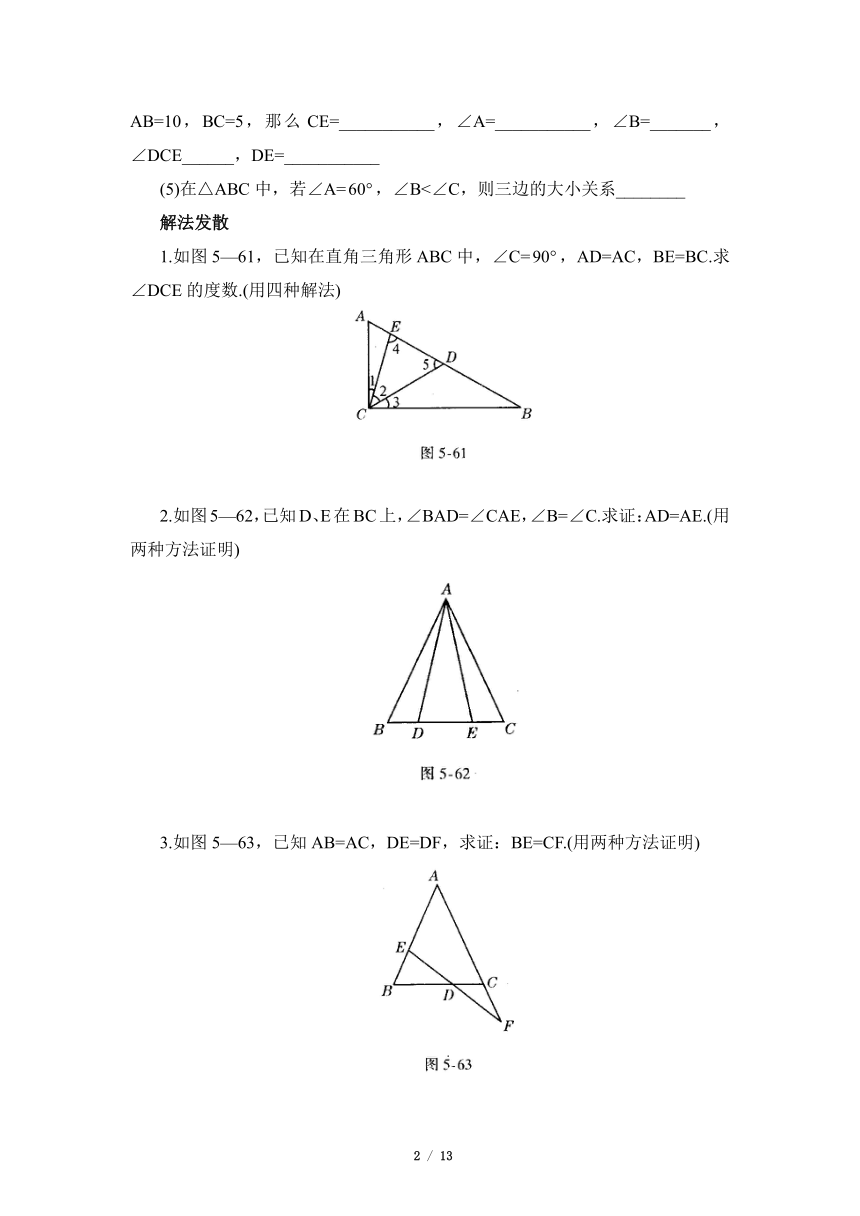
(4)在△ABC中,∠ACB=,CD⊥AB,垂足是D,E是AB的中点,如果AB=10,BC=5,那么CE=___________,∠A=___________,∠B=_______,∠DCE______,DE=___________
(5)在△ABC中,若∠A=,∠B<∠C,则三边的大小关系________
解法发散
1.如图5—61,已知在直角三角形ABC中,∠C=,AD=AC,BE=BC.求∠DCE的度数.(用四种解法)
2.如图5—62,已知D、E在BC上,∠BAD=∠CAE,∠B=∠C.求证:AD=AE.(用两种方法证明)
3.如图5—63,已知AB=AC,DE=DF,求证:BE=CF.(用两种方法证明)
变更命题发散
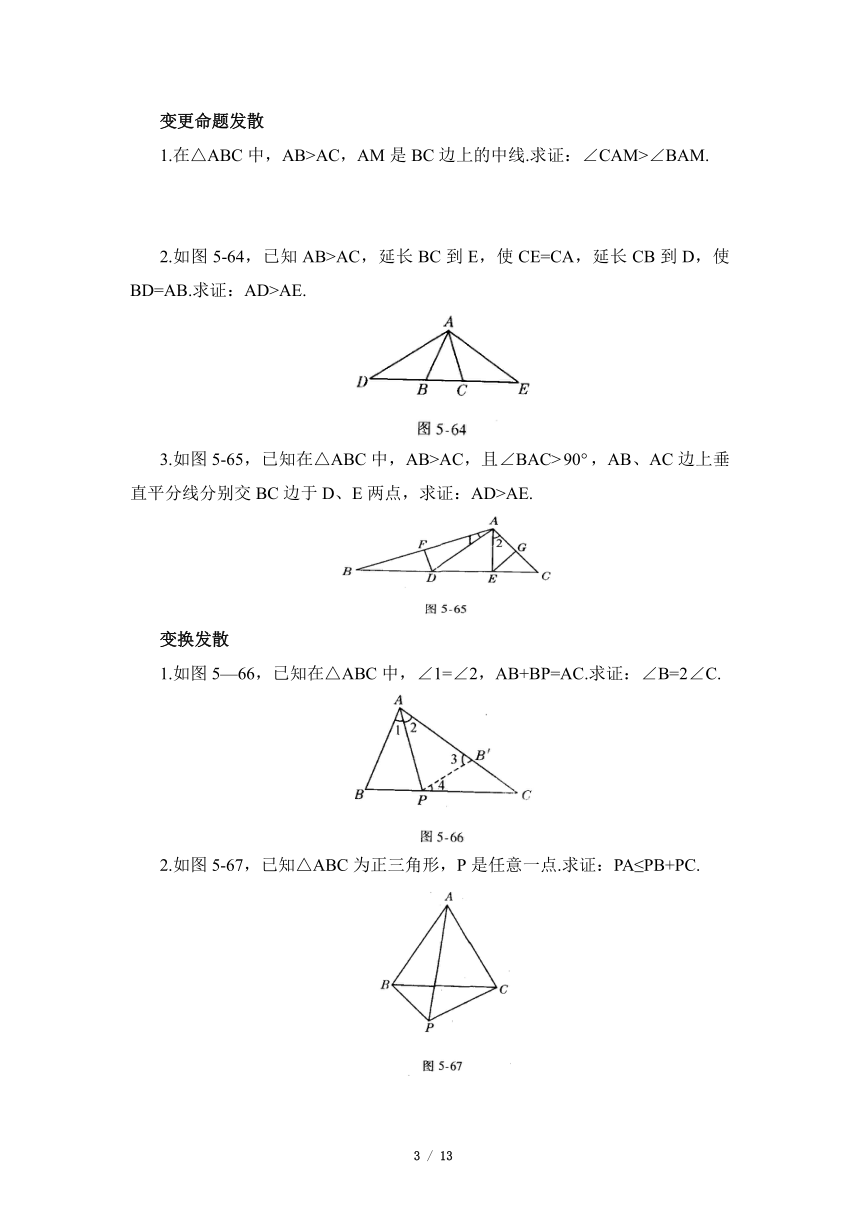
1.在△ABC中,AB>AC,AM是BC边上的中线.求证:∠CAM>∠BAM.
2.如图5-64,已知AB>AC,延长BC到E,使CE=CA,延长CB到D,使BD=AB.求证:AD>AE.
3.如图5-65,已知在△ABC中,AB>AC,且∠BAC>,AB、AC边上垂直平分线分别交BC边于D、E两点,求证:AD>AE.
变换发散
1.如图5—66,已知在△ABC中,∠1=∠2,AB+BP=AC.求证:∠B=2∠C.
2.如图5-67,已知△ABC为正三角形,P是任意一点.求证:PA≤PB+PC.
逆向发散
1.如图5—68,已知AD∥EC,CE>CB.求证:∠B>∠A.
2.如图5—69,在△ABC中,AB=AC,D为AC上一点.求证:∠ADB>∠ABD.
构造发散
1.如图5—70,在△ABC中,AB=AC.E是AB上任意一点,延长AC到F,使BE=CF.连接EF交BC于M,求证:EM=FM.
2.如图5—71,已知AE∥BC,AD、BD分别平分∠EAB、∠CBA,EC过点D.求证:AB=AE+BC.
纵横发散
1.如图5—72,△ABC为等边三角形,D、E分别是BC、AC上的一点,且BD=EC,AD和BE相交于F,BG⊥AD于G.求的值.
2.已知斜边和一锐角,作直角三角形.
已知:线段c及锐角α.求作Rt△ABC,使斜边等于c,其中—个锐角等于α.
综合发散
1.如图5—73所示,△ABC中,AB=AC,EF∥BC,分别交AB、AC于E、F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,连结BH与CG交于O.求证:
(1)BH=CG;
(2)AO平分∠BAC.
2.设AD是△ABC中∠A的平分线,过A引直线MN⊥AD,过B作BE⊥MN于E.求证:△EBC的周长大于△ABC的周长.
3.如图5—74,△ABC是等边三角形.∠ABE=∠BCF=∠CAD,求证:△DEF是等边三角形.
4.AD是△ABC中BC边上的中线,F是DC上—点,DE=EC,AC=BC,求证:AD平分∠BAE.
5.在△ABC中,AD是∠A的平分线且AB=AC+CD.求证:∠C=2∠B
参考答案
【巩固基础知识】
1.(1)(C)
(2)(C)
(3)(B)
(4)(C)
(5)(B)
2.(1)相等.
(2)2a.
(3)钝.
(4)5,,,,2.5.
(5)b解法发散
1.解法1∵AD=AC,∴∠5=∠2+∠1.
∴BE=BC,∴∠4=∠2+∠3.
∴∠A=-(∠5+∠1+∠2)=-2(∠1+∠2)①
同理∠B=-2(∠2+∠3).②
①+②得:2(∠1+∠2+∠3)+2∠2=-(∠A+∠B),
即+2∠2=-(∠A+∠B),
故∠2=∠DCE=.
解法2∵∠4=-∠B,∠5=-∠A,
∴∠4+∠5=-.
又∠2=-(∠4+∠5),
∴∠2=.
解法3∵∠4=∠1+∠A,∠4=-∠1,
∴∠1+∠A=-∠1.2∠1=-∠A即∠1=∠B.
同理∠3=∠A.
∠2=-(∠1+∠3)=.
解法4
-2∠4-2∠5=∠A+∠B,-2(∠4+∠5)=,
2(∠4+∠5)=,∠4+∠5=;
∴∠2=.
2.证法1在△ABC中,∵∠B=∠C,∴AC=AB.
在△ABD和△ACE中,
∵∠BAD=∠CAE,AB=AC,∠B=∠C,
∴△ABD≌△ACE.AD=AE.
证法2
在△ABD和△ACE中,
∵∠B=∠C,∠BAD=∠CAE,
∴∠ADB=∠AEC,
∴∠ADE=∠AED.AD=AE.
3.证法1如图,过E、F分别作BC的垂线,交BC和BC的延长线于M、N.
∵∠EMD=∠FND=,∠1=∠2,DE=DF,
∴△MDE≌△NDF,EM=FN.
∵AB=AC,
∴∠ABC=∠ACB=∠NCF.又∠EMB=∠ENC=,
∴Rt△EMB≌Rt△FNC.BE=CF.
证法2如图,在BC上取点G,使DG=DC,连结EG,则△EDG≌△FDC.
∴EG=CF,∠DEG=∠DFC.
∴EG∥AF,∠3=∠4.
又AB=AC,∴∠B=∠4.∴∠B=∠3.
∴BE=EG.BE=CF.
变更命题发散
1.分析:如图,延长AM至D,使AM=MD,通过证明△CMD≌△AMB,将∠BAM=∠CDM和∠CAM集中到同一个三角形ACD中,进行证明.
证明:延长AM到D,使MD=AM,连结CD,则△AMB≌△DMC.
∴∠1=∠D,AB=DC,∵AB>AC,
∴CD>AC.∠DAC>∠D.
故∠CAM>∠BAM.
2.∵AB>AC,∴∠ACB>∠ABC.
∴∠ABD>∠ACE.
又∵AB=BD.∴∠D=∠DAB=(-∠ABD),
同理得:∠E=(-∠ACE),
∴∠E>∠D.在△ADE中,
∵∠E>∠D,∴AD>AE.
3.在△ABC中,∵AB>AC,∴∠C>∠B,∴DF垂直平分AB,
∴AD=BD.∴∠B=∠1.同理∠C=∠2.
∵∠ADE=∠B+∠1=2∠B,∠AED=∠C+∠2=2∠C,
∴∠AED>∠ADE.AD>AE.
变换发散
1.分析:用对称法.本题利用角平分线是角的对称轴,在AC上截取,得到,从而构造与△ABP两个轴对称图形.
证明:在AC上截取连结.
∵AB=,∠1=∠2,AP=AP,∴△ABP≌△(SAS).
∴∠B=∠3,BP=.AB+BP=AC,,
∴AB+BP=.
又∵
∴∠4=∠C.∠B=∠3=2∠C.
2.分析:考虑本题是等边三角形,如图,以B为旋转中心,将△PBC旋转,则BC和BA重合,△BPC落到的位置,连.
∵,
∴为等边三角形.
∴,而与AP构成一个三角形,
∴AP<,即AP若∠BCP=∠BAP,则P为△ABC的外接圆上的一点,落在AP上.
∴BP+PC=AP.
证明:以B为顶点、BA为边作,以A为顶点、AB为边作=∠PCB,与交于,则.
∴,.
∵∠ABC=,=∠PBC,∴.
∴为等边三角形.
∴.若∠BAP≠∠BCP,则不落在AP上,
则在中,,
∴BP+PC>PA.若,
则落在AP上,这时,
∴PA≤BP+PC.
逆向发散
1.∵AD∥EC,
∴∠A=∠CEB.在△CEB中,
∵CE>CB,∴∠B>∠CEB.∴∠B>∠A.
2.在△CBD中,∠ADB>∠C.∵AB=AC,
∴∠ABC=∠C.∴∠ADB>∠BAC,
又∵∠ABC>∠ABD,
∴∠ADB>∠ABD.
构造发散
1.分析:本题通过作辅助线来构造全等三角形,过E作ED∥AC,那么∠1=∠2=∠B,BE=ED=CF,不难证得△EDM≌△FCM,于是EM=FM.
证明:过E作ED∥AC交BC于D.
∵ED∥AC(作法),
∴∠1=∠2(两直线平行,同位角相等),
∠EDM=∠FCM(两直线平行,内错角相等).
∵AB=AC(已知),∴∠B=∠2(等边对等角).
∴∠B=∠1(等量代换),EB=ED(等角对等边).
又∵EB=CF(已知).∴ED=CF.在△EDM与△FCM中,
∵ED=CF,∠EDM=∠FCM,∠EMD=∠EMC(对顶角相等),
∴△EDM≌△FCM(AAS).∴EM=FM.
2.分析:本题在BA上截取BF=BC,构造新△AFD,通过证明△ADF≌△ADE达到将线段AE的位置转移到AF,使得AB=AF+FB转化为AB=AE+BC.
证明在BA上截取BF=BC,连结DF.
在△BCD和△BFD中,∵BD=BD,∠CBD=∠FBD,CB=FB,
∴△BCD≌△BFD.∴∠BCD=∠BFD.
∵BC∥AE,∠C+∠E=.
又∠BFD+∠AFD=,
∴∠AFD=∠E.在△AFD和△AED中,
∵∠AFD=∠E,∠FAD=∠EAD,AD=AD,
∴△AFD≌△AED.∴AF=AE.
∵AB=AF+FB.AB=AE+BC.
纵横发散
1.解△ABC是等边三角形,∴AB=BC,∠ABD=∠BCE=.
又BD=CE.∴△ABD≌△BCE,∴∠BAD=∠CBE,
从而∠BFG=∠BAD+∠ABE=∠CBE+∠ABE=,
∠FBG=.∴BF=2FG,即的值为2.
2.作法图,
(1)作∠DBE=α.
(2)在BD上截取BA=c.
(3)过A作AC上BE交BE于C.
则△ABC为所求作的三角形.
证明:由作法得,∠DBE=α,BA=c,AC⊥BE,∠ACB=Rt∠.
∴△ABC即为所作的三角形.
综合发散
1.(1)证△AGC≌△AHB;
(2)证△AOB≌△AOC.
2.延长BE到,使=BE,连结.
3.∵△ABC是等边三角形,∴∠ABC=∠ABC=∠ACB=①
又∵∠ABE=∠BCF=∠CAD,②
①-②得:∠BAE=∠CBF=∠ACD.
∵∠EDF=∠CAD+∠DCA,∠DEF=∠ABE+∠BAE,∠DFE=∠FBC+∠BCF.
∴∠EDF=∠DEF=∠DFE.
∴△DEF是等边三角形.
4.如图,延长AE到F,使EF=AE,连接DF,则△DEF≌△CEA(SAS).
∴DF=AC,∠1=∠C,
∵BD=DC,AC=BC,
∴AC=CD=BD.
∴∠CAD=∠2,DF=BD=AC.
∵∠ADB=∠C+∠CAD,
∴∠ADB=∠1+∠2.
∴△ADB≌△ADF(SAS).
∴∠BAD=∠FAD,即AD平分∠BAE.
5.如图,在AB上截取AE=AC,连接DE,
∵AD平分∠A,
∴△ACD≌△AED.
∴CD=DE,∠ACD=∠AED.
∵AB=AC+CD,
∴DE=BE,∠EDB=∠EBD.
∴∠AED=2∠B,即∠ACB=2∠B.
1
/
13
三角形
【基础巩固训练】
题型发散
1.选择题,把正确答案的代号填入题中括号内.
(1)下列各条件中,不能作出惟一三角形的是(
)
(A)已知两角和夹边
(B)已知两边和夹角
(C)已知两边和其中一边的对角
(D)已知三边
(2)已知一个三角形的周长为15cm,且其中两边都等于第三边的2倍,那么这个三角形的最短边为(
)
(A)1cm
(B)2cm
(C)3cm
(D)4cm
(3)如果角形的一个内角等于其余两个内角的和,那么这个三角形是
(A)锐角三角形
(B)直角三角形
(C)钝角三角形
(D)锐角三角形或钝角三角形
(4)已知线段AB,用规尺作AB的垂直平分线CD,垂足为E,在CD上取—点F,使EF=AB,连结AF,BF,那么∠AFB的度数是(
)
(A)
(B)
(C)
(D)
(5)在Rt△ABC中,∠ACB=,CD⊥AB,E为AB的中点,AC=3cm,AB=6cm,那么∠DCE的度数是(
)
(A)
(B)
(C)
(D)
2.填空题.
(1)若两个三角形全等,则它们对应高、对应中线、对应的角平分线分别______________.
(2)在△ABC中,∠B=2∠C,AD⊥AC,交BC于D,若AB=a,则CD=______________.
(3)在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大,则这个三角形是__________角三角形.
(4)在△ABC中,∠ACB=,CD⊥AB,垂足是D,E是AB的中点,如果AB=10,BC=5,那么CE=___________,∠A=___________,∠B=_______,∠DCE______,DE=___________
(5)在△ABC中,若∠A=,∠B<∠C,则三边的大小关系________
解法发散
1.如图5—61,已知在直角三角形ABC中,∠C=,AD=AC,BE=BC.求∠DCE的度数.(用四种解法)
2.如图5—62,已知D、E在BC上,∠BAD=∠CAE,∠B=∠C.求证:AD=AE.(用两种方法证明)
3.如图5—63,已知AB=AC,DE=DF,求证:BE=CF.(用两种方法证明)
变更命题发散
1.在△ABC中,AB>AC,AM是BC边上的中线.求证:∠CAM>∠BAM.
2.如图5-64,已知AB>AC,延长BC到E,使CE=CA,延长CB到D,使BD=AB.求证:AD>AE.
3.如图5-65,已知在△ABC中,AB>AC,且∠BAC>,AB、AC边上垂直平分线分别交BC边于D、E两点,求证:AD>AE.
变换发散
1.如图5—66,已知在△ABC中,∠1=∠2,AB+BP=AC.求证:∠B=2∠C.
2.如图5-67,已知△ABC为正三角形,P是任意一点.求证:PA≤PB+PC.
逆向发散
1.如图5—68,已知AD∥EC,CE>CB.求证:∠B>∠A.
2.如图5—69,在△ABC中,AB=AC,D为AC上一点.求证:∠ADB>∠ABD.
构造发散
1.如图5—70,在△ABC中,AB=AC.E是AB上任意一点,延长AC到F,使BE=CF.连接EF交BC于M,求证:EM=FM.
2.如图5—71,已知AE∥BC,AD、BD分别平分∠EAB、∠CBA,EC过点D.求证:AB=AE+BC.
纵横发散
1.如图5—72,△ABC为等边三角形,D、E分别是BC、AC上的一点,且BD=EC,AD和BE相交于F,BG⊥AD于G.求的值.
2.已知斜边和一锐角,作直角三角形.
已知:线段c及锐角α.求作Rt△ABC,使斜边等于c,其中—个锐角等于α.
综合发散
1.如图5—73所示,△ABC中,AB=AC,EF∥BC,分别交AB、AC于E、F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,连结BH与CG交于O.求证:
(1)BH=CG;
(2)AO平分∠BAC.
2.设AD是△ABC中∠A的平分线,过A引直线MN⊥AD,过B作BE⊥MN于E.求证:△EBC的周长大于△ABC的周长.
3.如图5—74,△ABC是等边三角形.∠ABE=∠BCF=∠CAD,求证:△DEF是等边三角形.
4.AD是△ABC中BC边上的中线,F是DC上—点,DE=EC,AC=BC,求证:AD平分∠BAE.
5.在△ABC中,AD是∠A的平分线且AB=AC+CD.求证:∠C=2∠B
参考答案
【巩固基础知识】
1.(1)(C)
(2)(C)
(3)(B)
(4)(C)
(5)(B)
2.(1)相等.
(2)2a.
(3)钝.
(4)5,,,,2.5.
(5)b
1.解法1∵AD=AC,∴∠5=∠2+∠1.
∴BE=BC,∴∠4=∠2+∠3.
∴∠A=-(∠5+∠1+∠2)=-2(∠1+∠2)①
同理∠B=-2(∠2+∠3).②
①+②得:2(∠1+∠2+∠3)+2∠2=-(∠A+∠B),
即+2∠2=-(∠A+∠B),
故∠2=∠DCE=.
解法2∵∠4=-∠B,∠5=-∠A,
∴∠4+∠5=-.
又∠2=-(∠4+∠5),
∴∠2=.
解法3∵∠4=∠1+∠A,∠4=-∠1,
∴∠1+∠A=-∠1.2∠1=-∠A即∠1=∠B.
同理∠3=∠A.
∠2=-(∠1+∠3)=.
解法4
-2∠4-2∠5=∠A+∠B,-2(∠4+∠5)=,
2(∠4+∠5)=,∠4+∠5=;
∴∠2=.
2.证法1在△ABC中,∵∠B=∠C,∴AC=AB.
在△ABD和△ACE中,
∵∠BAD=∠CAE,AB=AC,∠B=∠C,
∴△ABD≌△ACE.AD=AE.
证法2
在△ABD和△ACE中,
∵∠B=∠C,∠BAD=∠CAE,
∴∠ADB=∠AEC,
∴∠ADE=∠AED.AD=AE.
3.证法1如图,过E、F分别作BC的垂线,交BC和BC的延长线于M、N.
∵∠EMD=∠FND=,∠1=∠2,DE=DF,
∴△MDE≌△NDF,EM=FN.
∵AB=AC,
∴∠ABC=∠ACB=∠NCF.又∠EMB=∠ENC=,
∴Rt△EMB≌Rt△FNC.BE=CF.
证法2如图,在BC上取点G,使DG=DC,连结EG,则△EDG≌△FDC.
∴EG=CF,∠DEG=∠DFC.
∴EG∥AF,∠3=∠4.
又AB=AC,∴∠B=∠4.∴∠B=∠3.
∴BE=EG.BE=CF.
变更命题发散
1.分析:如图,延长AM至D,使AM=MD,通过证明△CMD≌△AMB,将∠BAM=∠CDM和∠CAM集中到同一个三角形ACD中,进行证明.
证明:延长AM到D,使MD=AM,连结CD,则△AMB≌△DMC.
∴∠1=∠D,AB=DC,∵AB>AC,
∴CD>AC.∠DAC>∠D.
故∠CAM>∠BAM.
2.∵AB>AC,∴∠ACB>∠ABC.
∴∠ABD>∠ACE.
又∵AB=BD.∴∠D=∠DAB=(-∠ABD),
同理得:∠E=(-∠ACE),
∴∠E>∠D.在△ADE中,
∵∠E>∠D,∴AD>AE.
3.在△ABC中,∵AB>AC,∴∠C>∠B,∴DF垂直平分AB,
∴AD=BD.∴∠B=∠1.同理∠C=∠2.
∵∠ADE=∠B+∠1=2∠B,∠AED=∠C+∠2=2∠C,
∴∠AED>∠ADE.AD>AE.
变换发散
1.分析:用对称法.本题利用角平分线是角的对称轴,在AC上截取,得到,从而构造与△ABP两个轴对称图形.
证明:在AC上截取连结.
∵AB=,∠1=∠2,AP=AP,∴△ABP≌△(SAS).
∴∠B=∠3,BP=.AB+BP=AC,,
∴AB+BP=.
又∵
∴∠4=∠C.∠B=∠3=2∠C.
2.分析:考虑本题是等边三角形,如图,以B为旋转中心,将△PBC旋转,则BC和BA重合,△BPC落到的位置,连.
∵,
∴为等边三角形.
∴,而与AP构成一个三角形,
∴AP<,即AP
∴BP+PC=AP.
证明:以B为顶点、BA为边作,以A为顶点、AB为边作=∠PCB,与交于,则.
∴,.
∵∠ABC=,=∠PBC,∴.
∴为等边三角形.
∴.若∠BAP≠∠BCP,则不落在AP上,
则在中,,
∴BP+PC>PA.若,
则落在AP上,这时,
∴PA≤BP+PC.
逆向发散
1.∵AD∥EC,
∴∠A=∠CEB.在△CEB中,
∵CE>CB,∴∠B>∠CEB.∴∠B>∠A.
2.在△CBD中,∠ADB>∠C.∵AB=AC,
∴∠ABC=∠C.∴∠ADB>∠BAC,
又∵∠ABC>∠ABD,
∴∠ADB>∠ABD.
构造发散
1.分析:本题通过作辅助线来构造全等三角形,过E作ED∥AC,那么∠1=∠2=∠B,BE=ED=CF,不难证得△EDM≌△FCM,于是EM=FM.
证明:过E作ED∥AC交BC于D.
∵ED∥AC(作法),
∴∠1=∠2(两直线平行,同位角相等),
∠EDM=∠FCM(两直线平行,内错角相等).
∵AB=AC(已知),∴∠B=∠2(等边对等角).
∴∠B=∠1(等量代换),EB=ED(等角对等边).
又∵EB=CF(已知).∴ED=CF.在△EDM与△FCM中,
∵ED=CF,∠EDM=∠FCM,∠EMD=∠EMC(对顶角相等),
∴△EDM≌△FCM(AAS).∴EM=FM.
2.分析:本题在BA上截取BF=BC,构造新△AFD,通过证明△ADF≌△ADE达到将线段AE的位置转移到AF,使得AB=AF+FB转化为AB=AE+BC.
证明在BA上截取BF=BC,连结DF.
在△BCD和△BFD中,∵BD=BD,∠CBD=∠FBD,CB=FB,
∴△BCD≌△BFD.∴∠BCD=∠BFD.
∵BC∥AE,∠C+∠E=.
又∠BFD+∠AFD=,
∴∠AFD=∠E.在△AFD和△AED中,
∵∠AFD=∠E,∠FAD=∠EAD,AD=AD,
∴△AFD≌△AED.∴AF=AE.
∵AB=AF+FB.AB=AE+BC.
纵横发散
1.解△ABC是等边三角形,∴AB=BC,∠ABD=∠BCE=.
又BD=CE.∴△ABD≌△BCE,∴∠BAD=∠CBE,
从而∠BFG=∠BAD+∠ABE=∠CBE+∠ABE=,
∠FBG=.∴BF=2FG,即的值为2.
2.作法图,
(1)作∠DBE=α.
(2)在BD上截取BA=c.
(3)过A作AC上BE交BE于C.
则△ABC为所求作的三角形.
证明:由作法得,∠DBE=α,BA=c,AC⊥BE,∠ACB=Rt∠.
∴△ABC即为所作的三角形.
综合发散
1.(1)证△AGC≌△AHB;
(2)证△AOB≌△AOC.
2.延长BE到,使=BE,连结.
3.∵△ABC是等边三角形,∴∠ABC=∠ABC=∠ACB=①
又∵∠ABE=∠BCF=∠CAD,②
①-②得:∠BAE=∠CBF=∠ACD.
∵∠EDF=∠CAD+∠DCA,∠DEF=∠ABE+∠BAE,∠DFE=∠FBC+∠BCF.
∴∠EDF=∠DEF=∠DFE.
∴△DEF是等边三角形.
4.如图,延长AE到F,使EF=AE,连接DF,则△DEF≌△CEA(SAS).
∴DF=AC,∠1=∠C,
∵BD=DC,AC=BC,
∴AC=CD=BD.
∴∠CAD=∠2,DF=BD=AC.
∵∠ADB=∠C+∠CAD,
∴∠ADB=∠1+∠2.
∴△ADB≌△ADF(SAS).
∴∠BAD=∠FAD,即AD平分∠BAE.
5.如图,在AB上截取AE=AC,连接DE,
∵AD平分∠A,
∴△ACD≌△AED.
∴CD=DE,∠ACD=∠AED.
∵AB=AC+CD,
∴DE=BE,∠EDB=∠EBD.
∴∠AED=2∠B,即∠ACB=2∠B.
1
/
13
