鲁教版五四制七年级上册数学第一章 《三角形》单元测试5(Word版 含答案)
文档属性
| 名称 | 鲁教版五四制七年级上册数学第一章 《三角形》单元测试5(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 48.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 00:00:00 | ||
图片预览


文档简介
第一章
三角形
单元测试
(总分100?
时间60分钟)
?一、填空题:(每题3分,共30分)
?1.如果三角形的两边长分别为3cm和7cm,那么第三边长应大于_______
而小于_______,如果这个三角形中有两条边相等,那么它的周长是________.
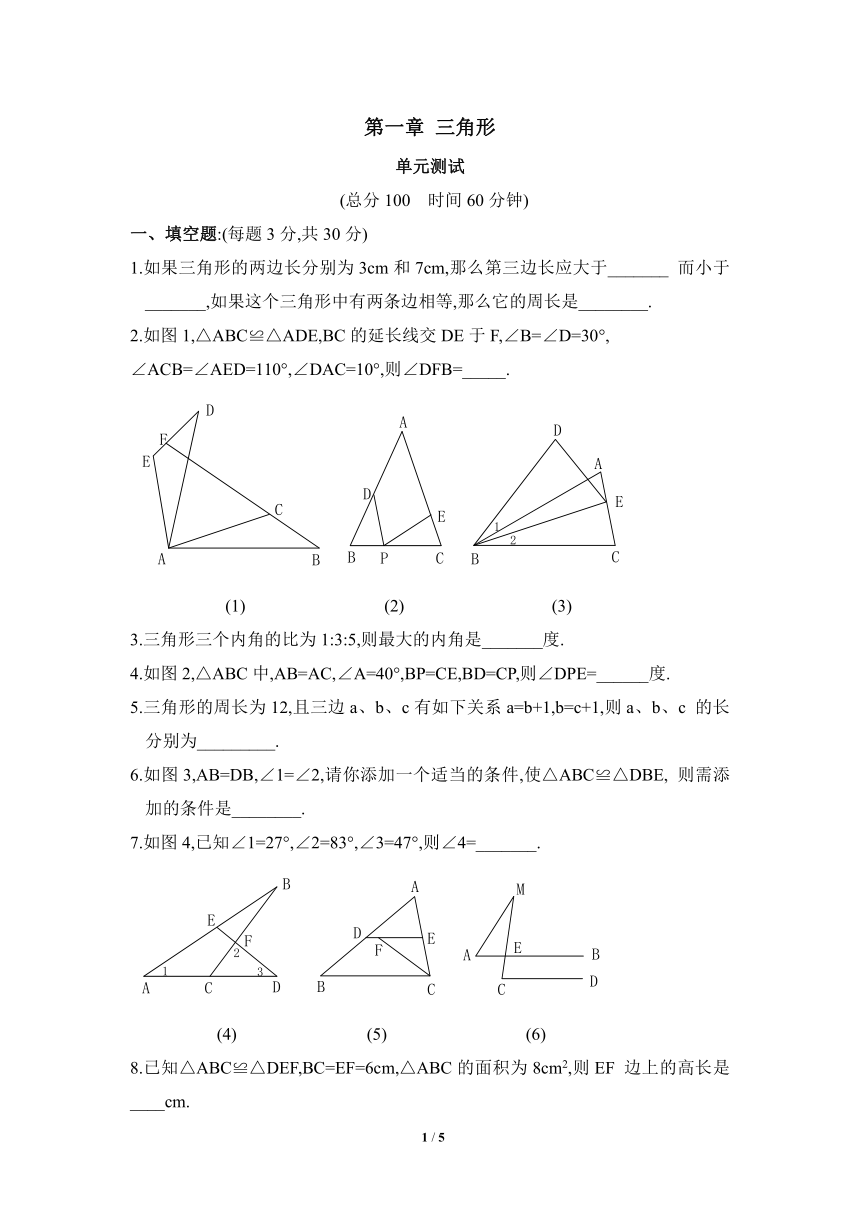
?2.如图1,△ABC≌△ADE,BC的延长线交DE于F,∠B=∠D=30°,
∠ACB=∠AED=110°,∠DAC=10°,则∠DFB=_____.
(1)
(2)
(3)
?3.三角形三个内角的比为1:3:5,则最大的内角是_______度.
?4.如图2,△ABC中,AB=AC,∠A=40°,BP=CE,BD=CP,则∠DPE=______度.
?5.三角形的周长为12,且三边a、b、c有如下关系a=b+1,b=c+1,则a、b、c
的长分别为_________.
?6.如图3,AB=DB,∠1=∠2,请你添加一个适当的条件,使△ABC≌△DBE,
则需添加的条件是________.
?7.如图4,已知∠1=27°,∠2=83°,∠3=47°,则∠4=_______.
(4)
(5)
(6)
?8.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为8cm2,则EF
边上的高长是____cm.
?9.AD和BE是△ABC中的高,H是AD与BE或是AD的延长线与EB的延长线的交点,
若BH=AC,则∠ABC=______.
?10.如图5,D、E分别是AB、AC的中点,∠ACB的平分线CF交DE于点F,若AC=6,则EF=________.
?二、选择题:(每题3分,共30分)
?11.长度为下列四组数的三条线段可构成三角形的是(
)
?
A.1,2,3?
B.4,6,11
C.5,6,7?
D.1.5,2.5,4.5
?12.如图6,AB∥CD,∠A=38°,∠C=80°,那么∠M等于(
)
?
A.52°?
B.42°?
C.10°?
D.40°
?13.如图7,AB∥CD,BC∥AD,AB=CD,BE=DF,其中全等三角形的对数是(
)
?
A.3?
B.4?
C.5?
D.6
(7)
(8)
(9)
?14.在△MNP中,Q为MN的中点,且PQ⊥MN,那么下列结论中不正确的是(
)
?
A.△MPQ≌△NPQ?
B.MP=NP
C.∠MPQ=∠NPQ?
D.MQ=NP
?15.△ABC的三个外角平分线所在直线相交构成一个△LMN,那么△LMN是(
)
?
A.直角三角形?
B.钝角三角形
?C.锐角三角形
D.等边三角形
?16.如图8,L1、L2、L3是三条互相平行的直线,且L1和L2的距离等于L2与L3
的距离,直线AB、CD分别交L1、L2、L3于A、O、B和C、O、D,连结BC,
则图中面积相等的三角形共有(
)
?
A.3对?
B.4对?
C.5对?
D.6对
?17.如图9,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面三个结论:①AS=AR
②QP∥AR
③△BRP≌△CSP正确的是(?
)
?
A.①和③?
B.②和③?
C.①和②?
D.①②和③
?18.△ABC中,如果∠A+∠B=2∠C,∠A≠∠B,则一定成立的是(
)
?
A.∠A、∠B、∠C都不等于60°?
B.∠A=60°
C.∠B=60°?????
D.∠C=60°
?19.下列命题错误的是(
)
?
A.有三边对应相等的两个三角形全;
B.有两边和它们的夹角对应相等的两个三角形全等
?
C.有两边和其中一边的对角对应相等的两个三角形全等
?
D.有两角和其中一角的对边对应相等的两个三角形全等
?20.如图,在△ABC中,已知∠B和∠C的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为(
)
?
A.9?
B.8?
C.7?
D.6
?三、解答题:(每题10分,共40分)
?21.已知Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC,求证:MN=AC.
?
22.已知:如图AC⊥BC,DC⊥EC,AC=BC,DC=EC,求证:∠D=∠E.
?
23.已知∠ABC=∠DAB=90°,AD+BC=CE,E为AB的中点,求证:∠DEC=90.
?
24.已知点C是AB上一点,△ACM、△CBN是等边三角形.
?
(1)请说明AN=BM.
?
(2)将△ACM绕点C按逆时针方向旋转180°,使A点能在CB上,
请对照原题图在右图画出符合要求的图形.
?
(3)若(2)所得到的图形中,结论“AN=BM”是否成立?若成立,请说明理由,
若不成立,也请说明理由.
?
(4)在(2)所得到的图形中,设MA的延长线与BN交于D点,请你判断△ABD的形状,
并说明你的理由.
?
参考答案
?1.4cm,10cm,17cm
2.50°
3.100
4.70
5.5,4,3
6.BE=BC或∠D=∠A
或∠DEB=∠C
7.23°
8.
9.45°或135°
10.3
?11.C
12.B
13.A
14.D
15.C
16.C
17.C
18.D
19.C
20.A
?21.连结CM,证△ACM≌△MNA
?22.证△DBC≌△EAC即可
?23.延长DE、CB,使之相交于F点,先由“AAS”证得△DAE≌△FBE得到AD=FB,DE=FE,再由AD+BC=CD
得FB+BC=CD
即FC=CD,结合已证结论DE=EF,可得CE⊥FD,
故得∠DEC=90°
?24.(1)证明△ACN≌△MCB(SAS)
(2)略
(3)成立,证△ACN≌△MCB
(4)△ABD是等边三角形,证略.
PAGE
1
/
5
三角形
单元测试
(总分100?
时间60分钟)
?一、填空题:(每题3分,共30分)
?1.如果三角形的两边长分别为3cm和7cm,那么第三边长应大于_______
而小于_______,如果这个三角形中有两条边相等,那么它的周长是________.
?2.如图1,△ABC≌△ADE,BC的延长线交DE于F,∠B=∠D=30°,
∠ACB=∠AED=110°,∠DAC=10°,则∠DFB=_____.
(1)
(2)
(3)
?3.三角形三个内角的比为1:3:5,则最大的内角是_______度.
?4.如图2,△ABC中,AB=AC,∠A=40°,BP=CE,BD=CP,则∠DPE=______度.
?5.三角形的周长为12,且三边a、b、c有如下关系a=b+1,b=c+1,则a、b、c
的长分别为_________.
?6.如图3,AB=DB,∠1=∠2,请你添加一个适当的条件,使△ABC≌△DBE,
则需添加的条件是________.
?7.如图4,已知∠1=27°,∠2=83°,∠3=47°,则∠4=_______.
(4)
(5)
(6)
?8.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为8cm2,则EF
边上的高长是____cm.
?9.AD和BE是△ABC中的高,H是AD与BE或是AD的延长线与EB的延长线的交点,
若BH=AC,则∠ABC=______.
?10.如图5,D、E分别是AB、AC的中点,∠ACB的平分线CF交DE于点F,若AC=6,则EF=________.
?二、选择题:(每题3分,共30分)
?11.长度为下列四组数的三条线段可构成三角形的是(
)
?
A.1,2,3?
B.4,6,11
C.5,6,7?
D.1.5,2.5,4.5
?12.如图6,AB∥CD,∠A=38°,∠C=80°,那么∠M等于(
)
?
A.52°?
B.42°?
C.10°?
D.40°
?13.如图7,AB∥CD,BC∥AD,AB=CD,BE=DF,其中全等三角形的对数是(
)
?
A.3?
B.4?
C.5?
D.6
(7)
(8)
(9)
?14.在△MNP中,Q为MN的中点,且PQ⊥MN,那么下列结论中不正确的是(
)
?
A.△MPQ≌△NPQ?
B.MP=NP
C.∠MPQ=∠NPQ?
D.MQ=NP
?15.△ABC的三个外角平分线所在直线相交构成一个△LMN,那么△LMN是(
)
?
A.直角三角形?
B.钝角三角形
?C.锐角三角形
D.等边三角形
?16.如图8,L1、L2、L3是三条互相平行的直线,且L1和L2的距离等于L2与L3
的距离,直线AB、CD分别交L1、L2、L3于A、O、B和C、O、D,连结BC,
则图中面积相等的三角形共有(
)
?
A.3对?
B.4对?
C.5对?
D.6对
?17.如图9,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面三个结论:①AS=AR
②QP∥AR
③△BRP≌△CSP正确的是(?
)
?
A.①和③?
B.②和③?
C.①和②?
D.①②和③
?18.△ABC中,如果∠A+∠B=2∠C,∠A≠∠B,则一定成立的是(
)
?
A.∠A、∠B、∠C都不等于60°?
B.∠A=60°
C.∠B=60°?????
D.∠C=60°
?19.下列命题错误的是(
)
?
A.有三边对应相等的两个三角形全;
B.有两边和它们的夹角对应相等的两个三角形全等
?
C.有两边和其中一边的对角对应相等的两个三角形全等
?
D.有两角和其中一角的对边对应相等的两个三角形全等
?20.如图,在△ABC中,已知∠B和∠C的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为(
)
?
A.9?
B.8?
C.7?
D.6
?三、解答题:(每题10分,共40分)
?21.已知Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC,求证:MN=AC.
?
22.已知:如图AC⊥BC,DC⊥EC,AC=BC,DC=EC,求证:∠D=∠E.
?
23.已知∠ABC=∠DAB=90°,AD+BC=CE,E为AB的中点,求证:∠DEC=90.
?
24.已知点C是AB上一点,△ACM、△CBN是等边三角形.
?
(1)请说明AN=BM.
?
(2)将△ACM绕点C按逆时针方向旋转180°,使A点能在CB上,
请对照原题图在右图画出符合要求的图形.
?
(3)若(2)所得到的图形中,结论“AN=BM”是否成立?若成立,请说明理由,
若不成立,也请说明理由.
?
(4)在(2)所得到的图形中,设MA的延长线与BN交于D点,请你判断△ABD的形状,
并说明你的理由.
?
参考答案
?1.4cm,10cm,17cm
2.50°
3.100
4.70
5.5,4,3
6.BE=BC或∠D=∠A
或∠DEB=∠C
7.23°
8.
9.45°或135°
10.3
?11.C
12.B
13.A
14.D
15.C
16.C
17.C
18.D
19.C
20.A
?21.连结CM,证△ACM≌△MNA
?22.证△DBC≌△EAC即可
?23.延长DE、CB,使之相交于F点,先由“AAS”证得△DAE≌△FBE得到AD=FB,DE=FE,再由AD+BC=CD
得FB+BC=CD
即FC=CD,结合已证结论DE=EF,可得CE⊥FD,
故得∠DEC=90°
?24.(1)证明△ACN≌△MCB(SAS)
(2)略
(3)成立,证△ACN≌△MCB
(4)△ABD是等边三角形,证略.
PAGE
1
/
5
