五年级上册数学一课一练-5.6解决问题 西师大版(2014秋)(含答案)
文档属性
| 名称 | 五年级上册数学一课一练-5.6解决问题 西师大版(2014秋)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 117.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览



文档简介
五年级上册数学一课一练-5.6解决问题
一、单选题
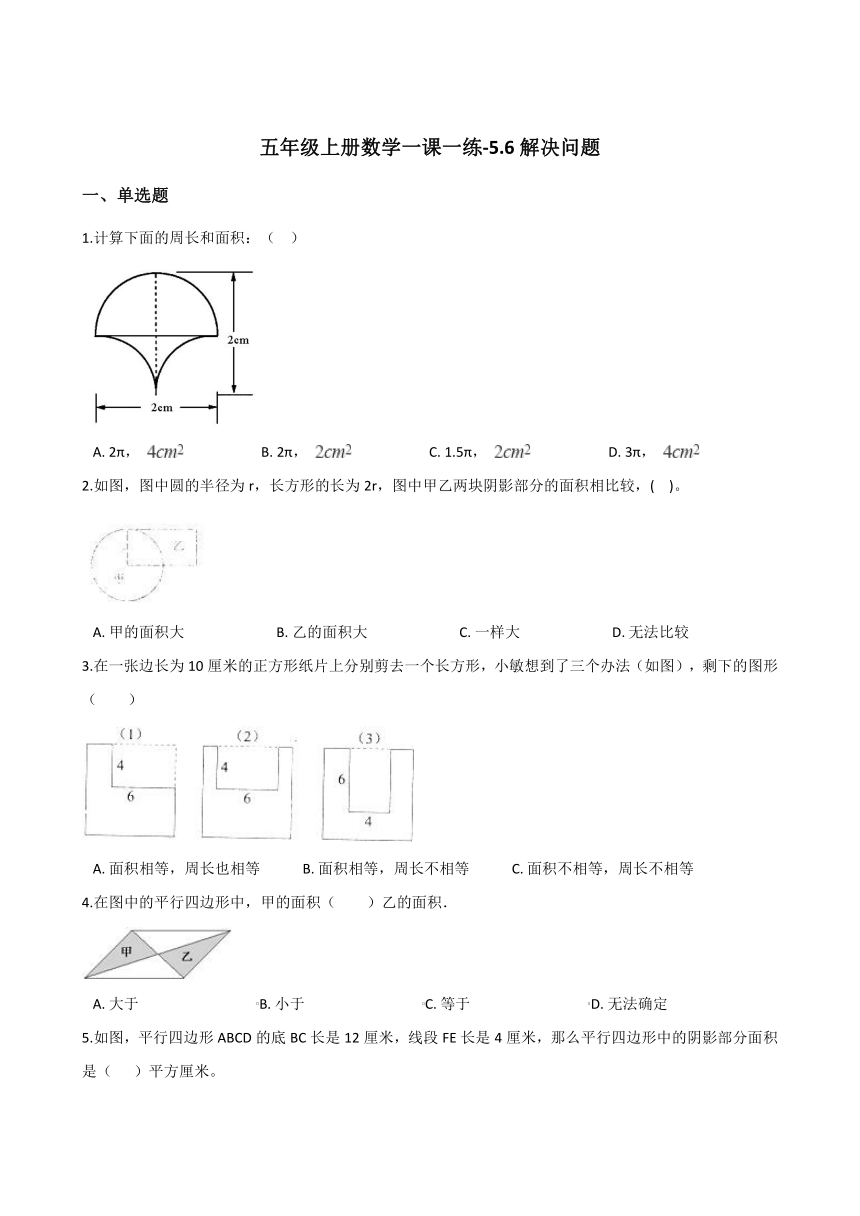
1.计算下面的周长和面积:(?? )
A.?2π, ??????????????????????B.?2π, ??????????????????????C.?1.5π, ??????????????????????D.?3π,
2.如图,图中圆的半径为r,长方形的长为2r,图中甲乙两块阴影部分的面积相比较,( ??)。
A.?甲的面积大??????????????????????????B.?乙的面积大??????????????????????????C.?一样大??????????????????????????D.?无法比较
3.在一张边长为10厘米的正方形纸片上分别剪去一个长方形,小敏想到了三个办法(如图),剩下的图形( )
A.?面积相等,周长也相等????????????B.?面积相等,周长不相等????????????C.?面积不相等,周长不相等
4.在图中的平行四边形中,甲的面积( )乙的面积.
A.?大于??????????????????????????????????B.?小于??????????????????????????????????C.?等于??????????????????????????????????D.?无法确定
5.如图,平行四边形ABCD的底BC长是12厘米,线段FE长是4厘米,那么平行四边形中的阴影部分面积是(???? )平方厘米。
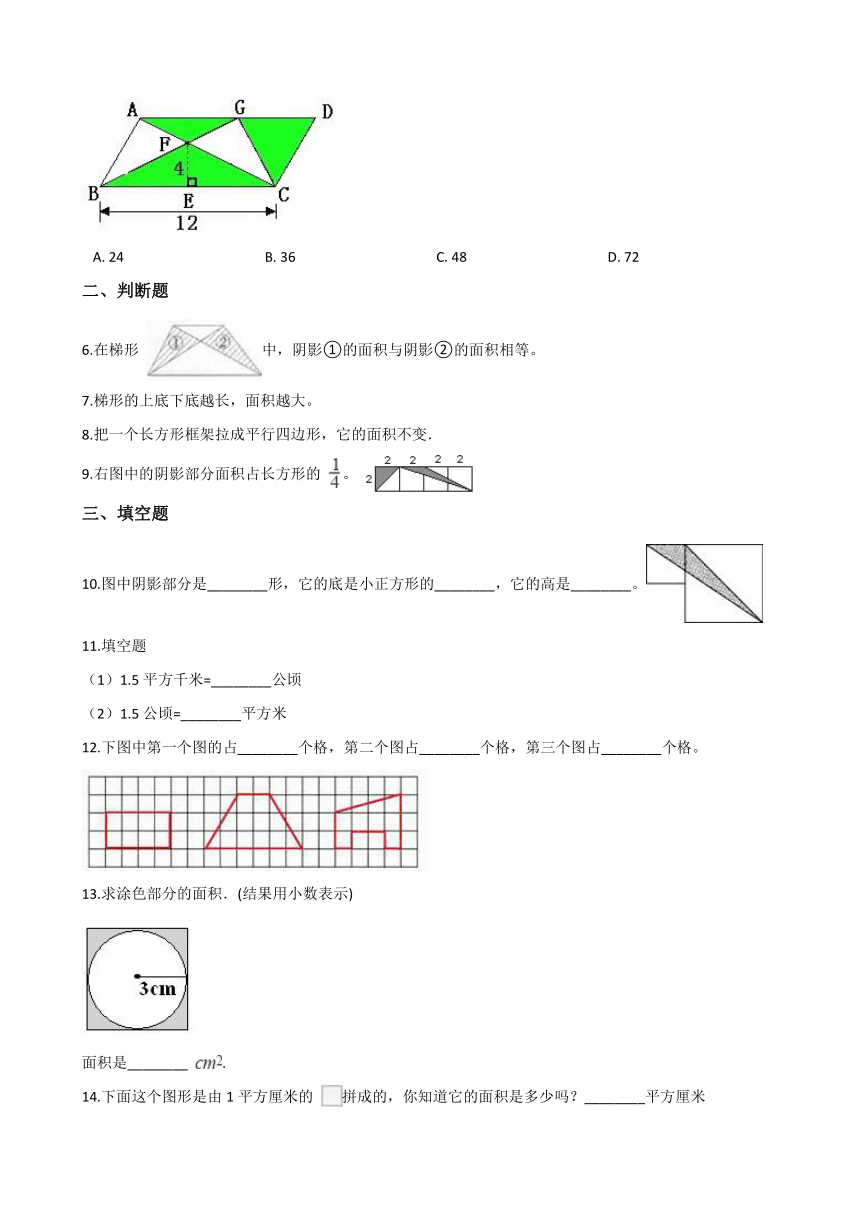
A.?24?????????????????????????????????????????B.?36?????????????????????????????????????????C.?48?????????????????????????????????????????D.?72
二、判断题
6.在梯形 中,阴影①的面积与阴影②的面积相等。
7.梯形的上底下底越长,面积越大。
8.把一个长方形框架拉成平行四边形,它的面积不变.
9.右图中的阴影部分面积占长方形的 。
三、填空题
10.图中阴影部分是________形,它的底是小正方形的________,它的高是________。
11.填空题
(1)1.5平方千米=________公顷
(2)1.5公顷=________平方米
12.下图中第一个图的占________个格,第二个图占________个格,第三个图占________个格。
13.求涂色部分的面积.(结果用小数表示)
面积是________ .
14.下面这个图形是由1平方厘米的 拼成的,你知道它的面积是多少吗?________平方厘米
15.把2个边长4厘米的正方形拼成一个长方形,这个长方形的周长是________厘米,面积是________平方厘米。
四、解答题
16.如图,正方形的边长是4厘米,求阴影部分的周长和面积.
五、综合题
17.图是小明家住房平面图.(单位:米)
(1)客厅的面积是多少平方米?
(2)厨房的面积比客厅少多少平方米?
(3)你还能提出什么数学问题?并尝试解决.
六、应用题
18.如图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是多少?
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:周长:π×2=2π(cm)
面积:2÷2=1(cm),2×1=2(cm2)
故答案为:B
【分析】这个图形的周长实际就是一个直径2cm的圆的周长,图形的面积实际就是长2cm、宽1cm的长方形的面积.
2.【答案】 A
【解析】【解答】解:甲的面积:π×r?×=2.355r?;乙的面积:2r×r=2r?;2.355r?>2r?,所以甲的面积大.
故答案为:A
【分析】甲的面积是所在圆面积的, 根据圆面积公式用含有r的式子表示甲的面积;根据长方形面积公式用式子表示出乙的面积;然后比较大小即可.
3.【答案】 B
【解析】【解答】(1)是从一个角上剪去一个长方形,剪去的两条边的长度等于又露出的两条边的长度,它的周长不变,面积比原来的面积减少了6×4=24平方厘米.(2)是从1条边上剪去一个长方形,周长比原来增加了4×2=8厘米,面积比原来减少了6×4=24平方厘米.(3)虽然也是从1条边上剪去一个长方形,但是周长比原来增加了6×2=12厘米,面积比原来减少了6×4=24平方厘米三种剪法剩下的面积相等,周长不相等.
故答案为:B
【分析】根据边长的变化进行分析.
4.【答案】C
【解析】【解答】解:因为三角形甲和上面的空白三角形与三角形乙和上面的空白三角形,组成了两个等底等高的大三角形,
都去掉公共部分,即上面的空白三角形,剩下的面积仍然相等,即甲的面积等于乙的面积;
故选:C.
【分析】由题意可知,三角形甲和上面的空白三角形与三角形乙和上面的空白三角形,组成了两个等底等高的大三角形,都去掉公共部分,即上面的空白三角形,剩下的面积仍然相等,即甲的面积等于乙的面积,据此解答即可.
5.【答案】C
【解析】【解答】解:因为△FAG与△CGD的面积之和与△FBC的面积相等,所以△GBC与△CAD的面积相等,阴影部分的总面积是:
12×4÷2×2
=48÷2×2
=48(平方厘米)
故答案为:C
【分析】先求出三角形BFC的面积,因为两个空白三角形的面积相等,所以三角形GBC与三角形CAD面积相等,都是四边形ABCD面积的一半,而三角形GFC是公共部分,所以三角形FAG与三角形CGD的面积之和与三角形FBC的面积相等,从而可以求出阴影部分的面积.
二、判断题
6.【答案】 正确
【解析】【解答】解:图中阴影①的面积与阴影②的面积相等。
故答案为:正确。
【分析】图中阴影①和下面白色三角形与阴影②和下面白色三角形等底等高,所以它们的面积相等,都去掉下面白色三角形,剩下的面积也相等,所以阴影①的面积与阴影②的面积相等。
7.【答案】错误
【解析】【解答】梯形的面积=(上底+下底)×高÷2 ,一个梯形面积的大小与上底下底之和、高有关系,因此梯形的上底下底越长,面积越大的说法是错误的。
故答案为:错误。
【分析】因为梯形的面积=(上底+下底)×高÷2 ,一个梯形面积的大小与上底下底之和、高的大小有关, 据此解答。
8.【答案】错误
【解析】【解答】解答:把一个长方形框架拉成平行四边形,它的面积发生变化.平行四边形的底和高与长方形的长和宽相比,发生了变化,面积也变了.故错误。
【分析】把一个长方形框架拉成平行四边形,周长不变,面积变小.
9.【答案】正确
【解析】【解答】解:(2×2÷2×2)÷(2×8)
=4÷16
=
原题计算正确.
故答案为:正确
【分析】两块阴影部分是等底等高的三角形,根据面积公式分别计算阴影部分的面积之和和长方形的面积,用阴影部分面积除以长方形面积即可.
三、填空题
10.【答案】三角;边长;大正方形的边长
【解析】【解答】图中阴影部分是三角形,它的底是小正方形的边长,它的高是大正方形的边长.
故答案为:三角;边长;大正方形的边长.【分析】观察图形可知,阴影部分是三角形,它的底是小正方形的边长,它的高是大正方形的边长,据此解答.
11.【答案】 (1)150
(2)15000
【解析】
12.【答案】8;12;8
【解析】【解答】4×2=8(格),(2+6)×3÷2=12(格),1×4÷2+1×4+2=2+4+2=8(格)。
故答案为:8、12、8
【分析】长方形面积=长×宽,梯形面积=(上底+下底)×高÷2,第三个图形按3个图形计算,上面是三角形,中间是长方形,下面是2格,它们的和就是组合图形面积。
13.【答案】7.74
【解析】【解答】3×2=6
6×6×-3×3×3.14=7.74(平方厘米)
【分析】圆的周长=圆周率×直径=圆周率×半径×2;圆的面积=圆周率×半径×半径.
14.【答案】 13
【解析】【解答】(1+3+5)×2-5=13(个);
1×1×13=13(平方厘米),
答:这个图形的面积是13平方厘米.
【分析】很显然可以看出,这个图形中一共有1+3+5+1+3=13(个)小正方形,由此用1个正方形的面积乘13即可求得这个图形的面积.
根据图形的得出图形中小正方形的个数,是解决本题的关键.
15.【答案】 24;32
【解析】【解答】(4×2+4)×2=12×2=24(厘米);4×2×4=32(平方厘米)。
故答案为:24;32.
【分析】长方形的长是4×2,宽是4,长方形周长=(长+宽)×2,长方形面积=长×宽。
四、解答题
16.【答案】解:周长:4×3.14=12.56(厘米)
面积:4×4﹣(4÷2)2×3.14
=16﹣12.56
=3.44(平方厘米)
答:阴影部分的周长是12.56厘米,面积是3.44平方厘米.
【解析】【分析】(1)观察图形可得,阴影部分的周长等于半径是4÷2=2厘米的圆的周长;(2)阴影部分的面积等于正方形的面积减去一个半径2厘米的圆的面积,即可解答.圆的面积=3.14×半径2 , 正方形的面积=边长×边长.
五、综合题
17.【答案】 (1)解:5.4×4.2=22.68(平方米),
答:客厅的面积是22.68平方米
(2)解:22.68﹣3.3×3.1
=22.68﹣10.23
=12.45(平方米),
答:厨房的面积比客厅少12.45平方米
(3)解:提问:卫生间的面积是多少?
3.6×2.0=7.2(平方米),
答:卫生间的面积是7.2平方米
【解析】【分析】(1)根据长方形的面积公式:S=ab,可求客厅的面积;(2)根据长方形的面积公式:S=ab,可求厨房的面积,再用客厅的面积减去厨房的面积即可;(3)根据图形提供的数据,可以求出其它房间的面积,比如:卫生间的面积是多少?再利用长方形的面积公式解决即可.此题主要考查了长方形的面积公式的实际应用.关键是正确判断长方形的长和宽.
六、应用题
18.【答案】解:因为长方形的面积等于△ABC与△ECD的面积和,
所以△ABC与△ECD重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,
即:S=49+35+13=97.
答:图中阴影部分的面积是97
【解析】【分析】所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分.因此,△ABC面积+△CDE面积+(13+49+35)=长方形面积+阴影部分面积.而△ABC的底是长方形的长,高是长方形的宽;△CDE的底是长方形的宽,高是长方形的长.因此,三角形ABC面积与三角形CDE面积,都是长方形面积的一半.本题主要考查对三角形和长方形面积的计算及其之间关系的掌握,以及观察分析能力.
一、单选题
1.计算下面的周长和面积:(?? )
A.?2π, ??????????????????????B.?2π, ??????????????????????C.?1.5π, ??????????????????????D.?3π,
2.如图,图中圆的半径为r,长方形的长为2r,图中甲乙两块阴影部分的面积相比较,( ??)。
A.?甲的面积大??????????????????????????B.?乙的面积大??????????????????????????C.?一样大??????????????????????????D.?无法比较
3.在一张边长为10厘米的正方形纸片上分别剪去一个长方形,小敏想到了三个办法(如图),剩下的图形( )
A.?面积相等,周长也相等????????????B.?面积相等,周长不相等????????????C.?面积不相等,周长不相等
4.在图中的平行四边形中,甲的面积( )乙的面积.
A.?大于??????????????????????????????????B.?小于??????????????????????????????????C.?等于??????????????????????????????????D.?无法确定
5.如图,平行四边形ABCD的底BC长是12厘米,线段FE长是4厘米,那么平行四边形中的阴影部分面积是(???? )平方厘米。
A.?24?????????????????????????????????????????B.?36?????????????????????????????????????????C.?48?????????????????????????????????????????D.?72
二、判断题
6.在梯形 中,阴影①的面积与阴影②的面积相等。
7.梯形的上底下底越长,面积越大。
8.把一个长方形框架拉成平行四边形,它的面积不变.
9.右图中的阴影部分面积占长方形的 。
三、填空题
10.图中阴影部分是________形,它的底是小正方形的________,它的高是________。
11.填空题
(1)1.5平方千米=________公顷
(2)1.5公顷=________平方米
12.下图中第一个图的占________个格,第二个图占________个格,第三个图占________个格。
13.求涂色部分的面积.(结果用小数表示)
面积是________ .
14.下面这个图形是由1平方厘米的 拼成的,你知道它的面积是多少吗?________平方厘米
15.把2个边长4厘米的正方形拼成一个长方形,这个长方形的周长是________厘米,面积是________平方厘米。
四、解答题
16.如图,正方形的边长是4厘米,求阴影部分的周长和面积.
五、综合题
17.图是小明家住房平面图.(单位:米)
(1)客厅的面积是多少平方米?
(2)厨房的面积比客厅少多少平方米?
(3)你还能提出什么数学问题?并尝试解决.
六、应用题
18.如图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是多少?
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:周长:π×2=2π(cm)
面积:2÷2=1(cm),2×1=2(cm2)
故答案为:B
【分析】这个图形的周长实际就是一个直径2cm的圆的周长,图形的面积实际就是长2cm、宽1cm的长方形的面积.
2.【答案】 A
【解析】【解答】解:甲的面积:π×r?×=2.355r?;乙的面积:2r×r=2r?;2.355r?>2r?,所以甲的面积大.
故答案为:A
【分析】甲的面积是所在圆面积的, 根据圆面积公式用含有r的式子表示甲的面积;根据长方形面积公式用式子表示出乙的面积;然后比较大小即可.
3.【答案】 B
【解析】【解答】(1)是从一个角上剪去一个长方形,剪去的两条边的长度等于又露出的两条边的长度,它的周长不变,面积比原来的面积减少了6×4=24平方厘米.(2)是从1条边上剪去一个长方形,周长比原来增加了4×2=8厘米,面积比原来减少了6×4=24平方厘米.(3)虽然也是从1条边上剪去一个长方形,但是周长比原来增加了6×2=12厘米,面积比原来减少了6×4=24平方厘米三种剪法剩下的面积相等,周长不相等.
故答案为:B
【分析】根据边长的变化进行分析.
4.【答案】C
【解析】【解答】解:因为三角形甲和上面的空白三角形与三角形乙和上面的空白三角形,组成了两个等底等高的大三角形,
都去掉公共部分,即上面的空白三角形,剩下的面积仍然相等,即甲的面积等于乙的面积;
故选:C.
【分析】由题意可知,三角形甲和上面的空白三角形与三角形乙和上面的空白三角形,组成了两个等底等高的大三角形,都去掉公共部分,即上面的空白三角形,剩下的面积仍然相等,即甲的面积等于乙的面积,据此解答即可.
5.【答案】C
【解析】【解答】解:因为△FAG与△CGD的面积之和与△FBC的面积相等,所以△GBC与△CAD的面积相等,阴影部分的总面积是:
12×4÷2×2
=48÷2×2
=48(平方厘米)
故答案为:C
【分析】先求出三角形BFC的面积,因为两个空白三角形的面积相等,所以三角形GBC与三角形CAD面积相等,都是四边形ABCD面积的一半,而三角形GFC是公共部分,所以三角形FAG与三角形CGD的面积之和与三角形FBC的面积相等,从而可以求出阴影部分的面积.
二、判断题
6.【答案】 正确
【解析】【解答】解:图中阴影①的面积与阴影②的面积相等。
故答案为:正确。
【分析】图中阴影①和下面白色三角形与阴影②和下面白色三角形等底等高,所以它们的面积相等,都去掉下面白色三角形,剩下的面积也相等,所以阴影①的面积与阴影②的面积相等。
7.【答案】错误
【解析】【解答】梯形的面积=(上底+下底)×高÷2 ,一个梯形面积的大小与上底下底之和、高有关系,因此梯形的上底下底越长,面积越大的说法是错误的。
故答案为:错误。
【分析】因为梯形的面积=(上底+下底)×高÷2 ,一个梯形面积的大小与上底下底之和、高的大小有关, 据此解答。
8.【答案】错误
【解析】【解答】解答:把一个长方形框架拉成平行四边形,它的面积发生变化.平行四边形的底和高与长方形的长和宽相比,发生了变化,面积也变了.故错误。
【分析】把一个长方形框架拉成平行四边形,周长不变,面积变小.
9.【答案】正确
【解析】【解答】解:(2×2÷2×2)÷(2×8)
=4÷16
=
原题计算正确.
故答案为:正确
【分析】两块阴影部分是等底等高的三角形,根据面积公式分别计算阴影部分的面积之和和长方形的面积,用阴影部分面积除以长方形面积即可.
三、填空题
10.【答案】三角;边长;大正方形的边长
【解析】【解答】图中阴影部分是三角形,它的底是小正方形的边长,它的高是大正方形的边长.
故答案为:三角;边长;大正方形的边长.【分析】观察图形可知,阴影部分是三角形,它的底是小正方形的边长,它的高是大正方形的边长,据此解答.
11.【答案】 (1)150
(2)15000
【解析】
12.【答案】8;12;8
【解析】【解答】4×2=8(格),(2+6)×3÷2=12(格),1×4÷2+1×4+2=2+4+2=8(格)。
故答案为:8、12、8
【分析】长方形面积=长×宽,梯形面积=(上底+下底)×高÷2,第三个图形按3个图形计算,上面是三角形,中间是长方形,下面是2格,它们的和就是组合图形面积。
13.【答案】7.74
【解析】【解答】3×2=6
6×6×-3×3×3.14=7.74(平方厘米)
【分析】圆的周长=圆周率×直径=圆周率×半径×2;圆的面积=圆周率×半径×半径.
14.【答案】 13
【解析】【解答】(1+3+5)×2-5=13(个);
1×1×13=13(平方厘米),
答:这个图形的面积是13平方厘米.
【分析】很显然可以看出,这个图形中一共有1+3+5+1+3=13(个)小正方形,由此用1个正方形的面积乘13即可求得这个图形的面积.
根据图形的得出图形中小正方形的个数,是解决本题的关键.
15.【答案】 24;32
【解析】【解答】(4×2+4)×2=12×2=24(厘米);4×2×4=32(平方厘米)。
故答案为:24;32.
【分析】长方形的长是4×2,宽是4,长方形周长=(长+宽)×2,长方形面积=长×宽。
四、解答题
16.【答案】解:周长:4×3.14=12.56(厘米)
面积:4×4﹣(4÷2)2×3.14
=16﹣12.56
=3.44(平方厘米)
答:阴影部分的周长是12.56厘米,面积是3.44平方厘米.
【解析】【分析】(1)观察图形可得,阴影部分的周长等于半径是4÷2=2厘米的圆的周长;(2)阴影部分的面积等于正方形的面积减去一个半径2厘米的圆的面积,即可解答.圆的面积=3.14×半径2 , 正方形的面积=边长×边长.
五、综合题
17.【答案】 (1)解:5.4×4.2=22.68(平方米),
答:客厅的面积是22.68平方米
(2)解:22.68﹣3.3×3.1
=22.68﹣10.23
=12.45(平方米),
答:厨房的面积比客厅少12.45平方米
(3)解:提问:卫生间的面积是多少?
3.6×2.0=7.2(平方米),
答:卫生间的面积是7.2平方米
【解析】【分析】(1)根据长方形的面积公式:S=ab,可求客厅的面积;(2)根据长方形的面积公式:S=ab,可求厨房的面积,再用客厅的面积减去厨房的面积即可;(3)根据图形提供的数据,可以求出其它房间的面积,比如:卫生间的面积是多少?再利用长方形的面积公式解决即可.此题主要考查了长方形的面积公式的实际应用.关键是正确判断长方形的长和宽.
六、应用题
18.【答案】解:因为长方形的面积等于△ABC与△ECD的面积和,
所以△ABC与△ECD重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,
即:S=49+35+13=97.
答:图中阴影部分的面积是97
【解析】【分析】所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分.因此,△ABC面积+△CDE面积+(13+49+35)=长方形面积+阴影部分面积.而△ABC的底是长方形的长,高是长方形的宽;△CDE的底是长方形的宽,高是长方形的长.因此,三角形ABC面积与三角形CDE面积,都是长方形面积的一半.本题主要考查对三角形和长方形面积的计算及其之间关系的掌握,以及观察分析能力.
