人教版八年级上册数学13.1.2《线段的垂直平分线》课时提升作业(Word版 含解析)
文档属性
| 名称 | 人教版八年级上册数学13.1.2《线段的垂直平分线》课时提升作业(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1009.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 22:09:10 | ||
图片预览




文档简介
《线段的垂直平分线》课时提升作业
一.选择题.
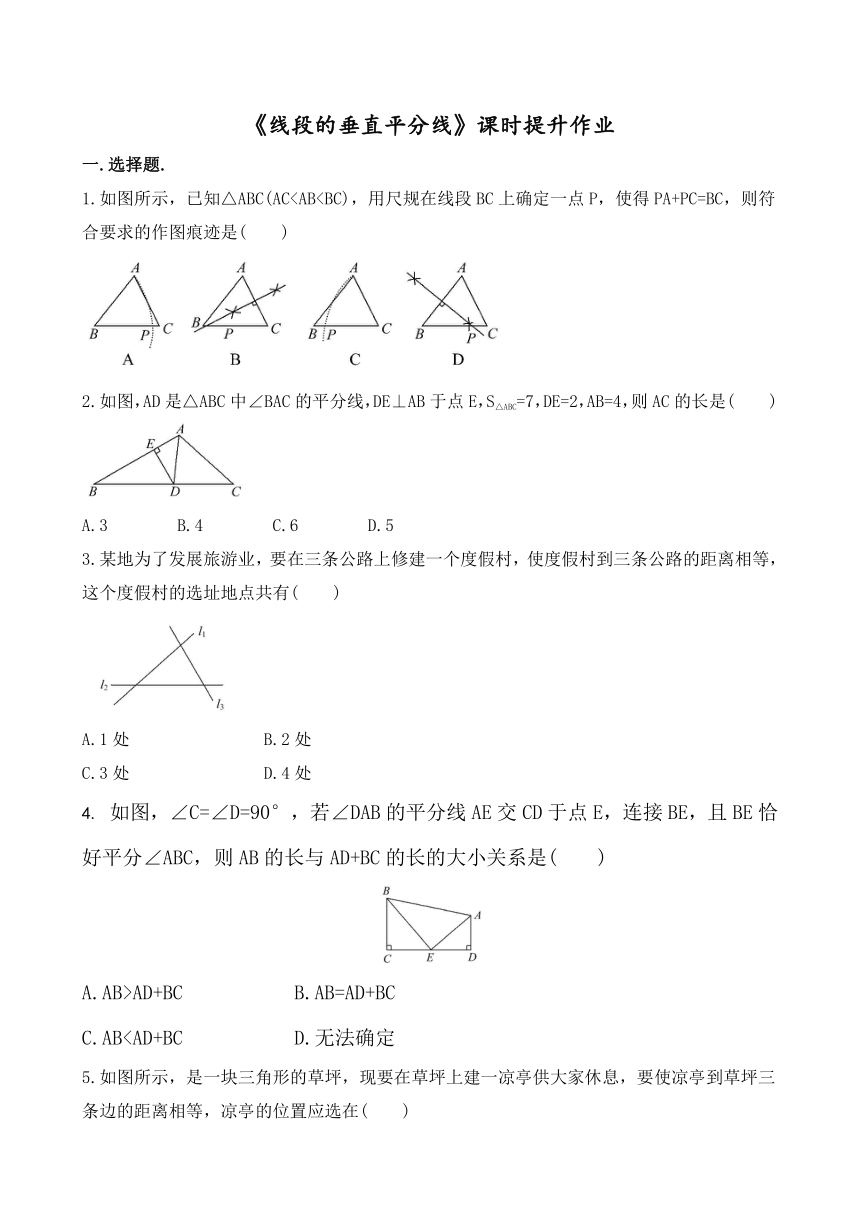
1.如图所示,已知△ABC(AC2.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.6 D.5
3.某地为了发展旅游业,要在三条公路上修建一个度假村,使度假村到三条公路的距离相等,这个度假村的选址地点共有( )
A.1处
B.2处
C.3处
D.4处
4.
如图,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则AB的长与AD+BC的长的大小关系是( )
A.AB>AD+BC
B.AB=AD+BC
C.ABD.无法确定
5.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
二.填空题(每小题4分,共12分)
1.阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.已知:线段AB.
小芸的作法如下:如图,(1)分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C,D两点.(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是________________.
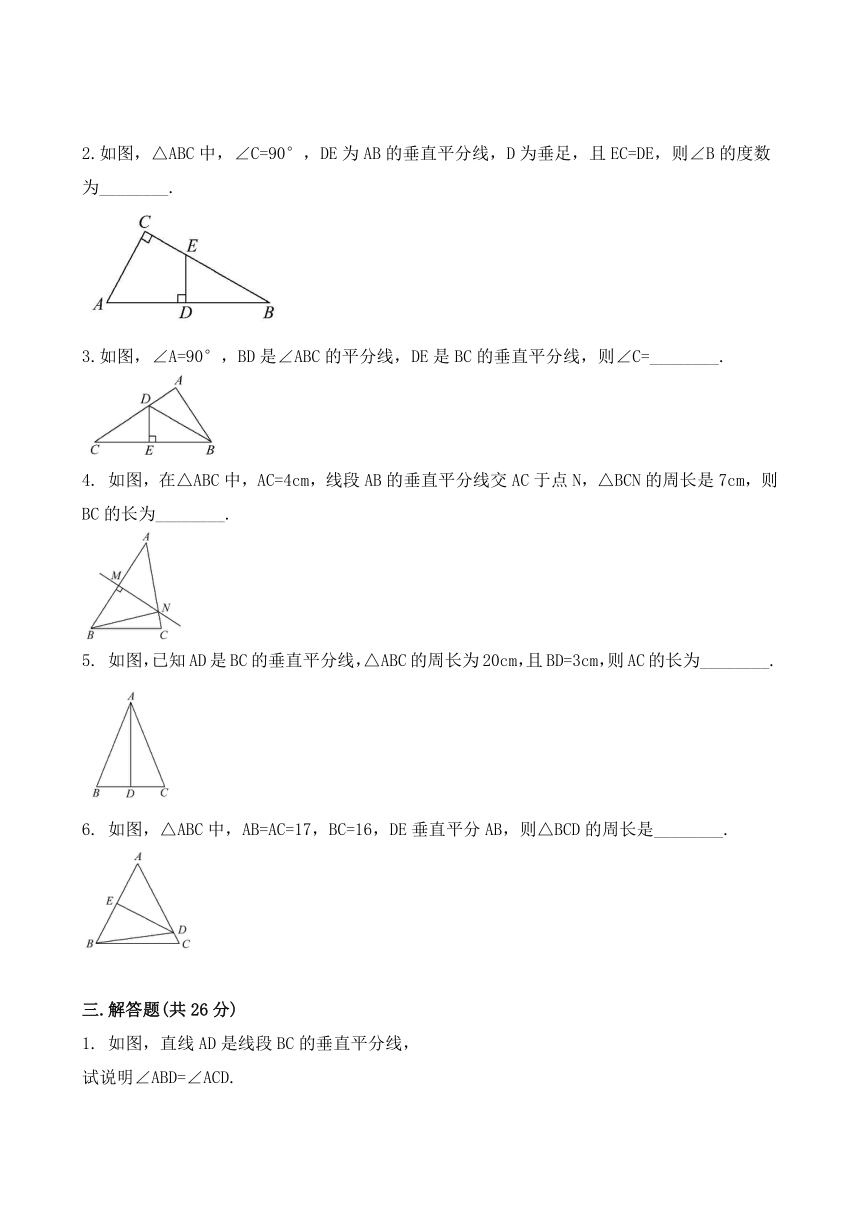
2.如图,△ABC中,∠C=90°,DE为AB的垂直平分线,D为垂足,且EC=DE,则∠B的度数为________.
3.如图,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,则∠C=________.
4.
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为________.
5.
如图,已知AD是BC的垂直平分线,△ABC的周长为20cm,且BD=3cm,则AC的长为________.
6.
如图,△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是________.
三.解答题(共26分)
1.
如图,直线AD是线段BC的垂直平分线,
试说明∠ABD=∠ACD.
2.如图,已知△ABC中,∠C为直角,AC(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹).
(2)连接AD,若∠B=37°,求∠CAD的度数.
3.如图,现有一块三角形的空地,其三条边长分别是20m,30
m,40
m.现要把它分成面积比为2∶3∶4的三部分,分别种植不同种类的花,请你设计一种方案,并简单说明理由.
4.如图:A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两地,问该站建在河边什么地方,可使所修的渠道到A,B两个蓄水池的距离相等,试在图中确定该点.(保留作图痕迹)
《线段的垂直平分线》课时提升作业(答案版)
一.选择题.
1.如图所示,已知△ABC(AC【解析】选D.假设点P在BC上存在,由PA+PC=BC,可得PA=PB,于是点P在AB垂直平分线上.
2.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.6 D.5
【解析】选A.如图,过点D作DF⊥AC于点F,
因为AD是△ABC中∠BAC的平分线,DE⊥AB,
所以DE=DF,由图可知,S△ABC=S△ABD+S△ACD,
所以×4×2+×AC×2=7,解得AC=3.
3.某地为了发展旅游业,要在三条公路上修建一个度假村,使度假村到三条公路的距离相等,这个度假村的选址地点共有( )
A.1处
B.2处
C.3处
D.4处
【解析】选D.如图,度假村在三角形内部时,为三角形的内心,只有1个,在外部时,为外角平分线的交点,共有3个,所以,这个度假村的选址地点共有P1,P2,P3,P44处.
【方法技巧】有关到线段距离相等的点的位置确定方法
1.当点指定在三角形内部时,只要作出内角的平分线的交点即可.
2.在点没有指定在三角形内部时,要注意画出内角平分线的交点和外角平分线的交点,这时交点有多个.
4.
如图,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则AB的长与AD+BC的长的大小关系是( )
A.AB>AD+BC
B.AB=AD+BC
C.ABD.无法确定
【解析】选B.过点E作EF⊥AB于F,
因为BE,AE分别为∠ABC和∠DAB的平分线,
∠C=∠D=90°,
所以EC=EF=ED,
所以△BCE≌△BFE,△AEF≌△AED,
所以BC=BF,AF=AD,
所以AB=AF+BF=AD+BC.
5.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
【解析】选C.到三角形两条边的距离相等的点在这两边的夹角的平分线上,所以到三角形三条边的距离都相等的点是这个三角形的三条角平分线的交点.
二.填空题(每小题4分,共12分)
1.阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.已知:线段AB.
小芸的作法如下:如图,(1)分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C,D两点.(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是________________.
【解析】到两端点的距离相等的点在线段的垂直平分线上,两点确定一条直线.
答案:到两端点的距离相等的点在线段的垂直平分线上,两点确定一条直线
2.如图,△ABC中,∠C=90°,DE为AB的垂直平分线,D为垂足,且EC=DE,则∠B的度数为________.
【解析】连接AE,
因为EC=DE,∠C=90°,
DE⊥AB,
所以∠CAE=∠DAE,
因为DE为AB的垂直平分线,所以AE=BE,
所以∠B=∠DAE,所以∠B=∠CAE=∠DAE,
在△ABC中,∠B+∠CAE+∠DAE=90°,
所以∠B=30°.
答案:30°
3.如图,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,则∠C=________.
【解析】因为DE垂直平分BC,所以∠C=∠DBC.又因为BD是∠ABC的平分线,所以∠ABD=∠DBC,所以∠ABC=2∠C.
因为∠A=90°,所以∠ABC+∠C=90°,即3∠C=90°,所以∠C=30°.
答案:30°
4.
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为________.
【解析】线段垂直平分线上的点到线段两端点的距离相等,所以AN=BN,所以△BCN的周长=BC+CN+BN=BC+AN+CN=BC+AC=BC+4=7,所以BC=3
cm.
5.
如图,已知AD是BC的垂直平分线,△ABC的周长为20cm,且BD=3cm,则AC的长为________.
【解析】因为AD是BC的垂直平分线,BD=3cm,
所以AB=AC,BC=6cm.
因为△ABC的周长为20cm,所以AC=7cm.
答案:7cm
6.
如图,△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是________.
【解析】因为DE垂直平分AB,所以BD=AD,
△BCD的周长为:BD+DC+BC=AD+DC+BC=AC+BC=17+16=33.
答案:33
三.解答题(共26分)
1.
如图,直线AD是线段BC的垂直平分线,
试说明∠ABD=∠ACD.
【解析】因为AD是线段BC的垂直平分线,
所以AB=AC,BD=CD.
又因为AD=AD,所以△ABD≌△ACD(SSS).
所以∠ABD=∠ACD.
2.如图,已知△ABC中,∠C为直角,AC(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹).
(2)连接AD,若∠B=37°,求∠CAD的度数.
【解析】(1)点D的位置如图所示(D为AB中垂线与BC的交点).
(2)因为在Rt△ABC中,∠B=37°,所以∠CAB=53°.
又因为AD=BD,所以∠BAD=∠B=37°.
所以∠CAD=53°-37°=16°.
3.如图,现有一块三角形的空地,其三条边长分别是20m,30
m,40
m.现要把它分成面积比为2∶3∶4的三部分,分别种植不同种类的花,请你设计一种方案,并简单说明理由.
【解析】分别作∠C和∠B的平分线,相交于点P.连接PA,则△PAB,△PAC,△PBC的面积之比为2∶3∶4(如图所示).理由如下:
因为P是∠ABC和∠ACB平分线上的点,过点P分别作PE⊥AB于点E,作PF⊥AC于点F,作PH⊥BC于点H,则PE=PF=PH.
所以S△PAB=AB·PE=10PE,
S△PAC=PF·AC=15PF,
S△PBC=PH·BC=20PH.
所以S△PAB∶S△PAC∶S△PBC=2∶3∶4.
4.如图:A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两地,问该站建在河边什么地方,可使所修的渠道到A,B两个蓄水池的距离相等,试在图中确定该点.(保留作图痕迹)
【解析】如图所示,连接AB,
作AB的垂直平分线CD,
CD与河流a的交点即为抽水站P的位置.
PAGE
一.选择题.
1.如图所示,已知△ABC(AC
A.3 B.4 C.6 D.5
3.某地为了发展旅游业,要在三条公路上修建一个度假村,使度假村到三条公路的距离相等,这个度假村的选址地点共有( )
A.1处
B.2处
C.3处
D.4处
4.
如图,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则AB的长与AD+BC的长的大小关系是( )
A.AB>AD+BC
B.AB=AD+BC
C.AB
5.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
二.填空题(每小题4分,共12分)
1.阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.已知:线段AB.
小芸的作法如下:如图,(1)分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C,D两点.(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是________________.
2.如图,△ABC中,∠C=90°,DE为AB的垂直平分线,D为垂足,且EC=DE,则∠B的度数为________.
3.如图,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,则∠C=________.
4.
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为________.
5.
如图,已知AD是BC的垂直平分线,△ABC的周长为20cm,且BD=3cm,则AC的长为________.
6.
如图,△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是________.
三.解答题(共26分)
1.
如图,直线AD是线段BC的垂直平分线,
试说明∠ABD=∠ACD.
2.如图,已知△ABC中,∠C为直角,AC
(2)连接AD,若∠B=37°,求∠CAD的度数.
3.如图,现有一块三角形的空地,其三条边长分别是20m,30
m,40
m.现要把它分成面积比为2∶3∶4的三部分,分别种植不同种类的花,请你设计一种方案,并简单说明理由.
4.如图:A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两地,问该站建在河边什么地方,可使所修的渠道到A,B两个蓄水池的距离相等,试在图中确定该点.(保留作图痕迹)
《线段的垂直平分线》课时提升作业(答案版)
一.选择题.
1.如图所示,已知△ABC(AC
2.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.6 D.5
【解析】选A.如图,过点D作DF⊥AC于点F,
因为AD是△ABC中∠BAC的平分线,DE⊥AB,
所以DE=DF,由图可知,S△ABC=S△ABD+S△ACD,
所以×4×2+×AC×2=7,解得AC=3.
3.某地为了发展旅游业,要在三条公路上修建一个度假村,使度假村到三条公路的距离相等,这个度假村的选址地点共有( )
A.1处
B.2处
C.3处
D.4处
【解析】选D.如图,度假村在三角形内部时,为三角形的内心,只有1个,在外部时,为外角平分线的交点,共有3个,所以,这个度假村的选址地点共有P1,P2,P3,P44处.
【方法技巧】有关到线段距离相等的点的位置确定方法
1.当点指定在三角形内部时,只要作出内角的平分线的交点即可.
2.在点没有指定在三角形内部时,要注意画出内角平分线的交点和外角平分线的交点,这时交点有多个.
4.
如图,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则AB的长与AD+BC的长的大小关系是( )
A.AB>AD+BC
B.AB=AD+BC
C.AB
【解析】选B.过点E作EF⊥AB于F,
因为BE,AE分别为∠ABC和∠DAB的平分线,
∠C=∠D=90°,
所以EC=EF=ED,
所以△BCE≌△BFE,△AEF≌△AED,
所以BC=BF,AF=AD,
所以AB=AF+BF=AD+BC.
5.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
【解析】选C.到三角形两条边的距离相等的点在这两边的夹角的平分线上,所以到三角形三条边的距离都相等的点是这个三角形的三条角平分线的交点.
二.填空题(每小题4分,共12分)
1.阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.已知:线段AB.
小芸的作法如下:如图,(1)分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C,D两点.(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是________________.
【解析】到两端点的距离相等的点在线段的垂直平分线上,两点确定一条直线.
答案:到两端点的距离相等的点在线段的垂直平分线上,两点确定一条直线
2.如图,△ABC中,∠C=90°,DE为AB的垂直平分线,D为垂足,且EC=DE,则∠B的度数为________.
【解析】连接AE,
因为EC=DE,∠C=90°,
DE⊥AB,
所以∠CAE=∠DAE,
因为DE为AB的垂直平分线,所以AE=BE,
所以∠B=∠DAE,所以∠B=∠CAE=∠DAE,
在△ABC中,∠B+∠CAE+∠DAE=90°,
所以∠B=30°.
答案:30°
3.如图,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,则∠C=________.
【解析】因为DE垂直平分BC,所以∠C=∠DBC.又因为BD是∠ABC的平分线,所以∠ABD=∠DBC,所以∠ABC=2∠C.
因为∠A=90°,所以∠ABC+∠C=90°,即3∠C=90°,所以∠C=30°.
答案:30°
4.
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为________.
【解析】线段垂直平分线上的点到线段两端点的距离相等,所以AN=BN,所以△BCN的周长=BC+CN+BN=BC+AN+CN=BC+AC=BC+4=7,所以BC=3
cm.
5.
如图,已知AD是BC的垂直平分线,△ABC的周长为20cm,且BD=3cm,则AC的长为________.
【解析】因为AD是BC的垂直平分线,BD=3cm,
所以AB=AC,BC=6cm.
因为△ABC的周长为20cm,所以AC=7cm.
答案:7cm
6.
如图,△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是________.
【解析】因为DE垂直平分AB,所以BD=AD,
△BCD的周长为:BD+DC+BC=AD+DC+BC=AC+BC=17+16=33.
答案:33
三.解答题(共26分)
1.
如图,直线AD是线段BC的垂直平分线,
试说明∠ABD=∠ACD.
【解析】因为AD是线段BC的垂直平分线,
所以AB=AC,BD=CD.
又因为AD=AD,所以△ABD≌△ACD(SSS).
所以∠ABD=∠ACD.
2.如图,已知△ABC中,∠C为直角,AC
(2)连接AD,若∠B=37°,求∠CAD的度数.
【解析】(1)点D的位置如图所示(D为AB中垂线与BC的交点).
(2)因为在Rt△ABC中,∠B=37°,所以∠CAB=53°.
又因为AD=BD,所以∠BAD=∠B=37°.
所以∠CAD=53°-37°=16°.
3.如图,现有一块三角形的空地,其三条边长分别是20m,30
m,40
m.现要把它分成面积比为2∶3∶4的三部分,分别种植不同种类的花,请你设计一种方案,并简单说明理由.
【解析】分别作∠C和∠B的平分线,相交于点P.连接PA,则△PAB,△PAC,△PBC的面积之比为2∶3∶4(如图所示).理由如下:
因为P是∠ABC和∠ACB平分线上的点,过点P分别作PE⊥AB于点E,作PF⊥AC于点F,作PH⊥BC于点H,则PE=PF=PH.
所以S△PAB=AB·PE=10PE,
S△PAC=PF·AC=15PF,
S△PBC=PH·BC=20PH.
所以S△PAB∶S△PAC∶S△PBC=2∶3∶4.
4.如图:A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两地,问该站建在河边什么地方,可使所修的渠道到A,B两个蓄水池的距离相等,试在图中确定该点.(保留作图痕迹)
【解析】如图所示,连接AB,
作AB的垂直平分线CD,
CD与河流a的交点即为抽水站P的位置.
PAGE
