苏科版初中数学八年级上册第3章 《勾股定理》学案及课堂练习(无答案)
文档属性
| 名称 | 苏科版初中数学八年级上册第3章 《勾股定理》学案及课堂练习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 344.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 08:05:41 | ||
图片预览

文档简介
苏科版初中数学八年级上册第3章
《勾股定理》教学设计及课堂练习
3.1勾股定理(1)
1、
自主先学:
1.我们已经学过三角形的一些基本知识,如果一个三角形的两条边分别长3和4,你知道第三边的长吗?你知道第三边长的范围吗?
2.如果又已知这两边的夹角是90度,那么第三边的长确定吗?
3.已知直角三角形的两边的长,如何求第三边的长呢?
2、
合作助学:
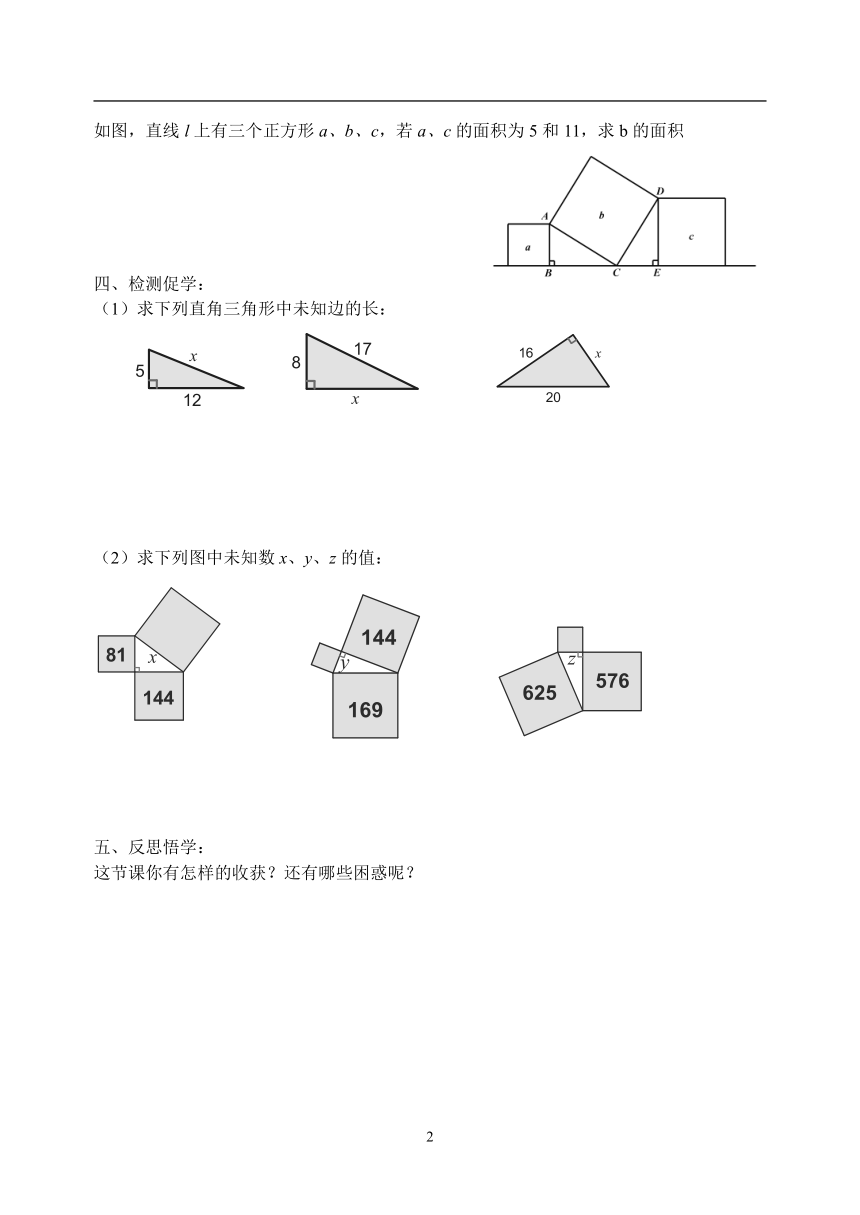
操作1:运算推演证实我们的猜想:为了计算面积方便,我们可将这将三角形放在方格纸中.如果每一个小方格的边长记作“1”,
我们曾经利用图形面积探索过数学公式,根据经验我们可以将探求边长之间的关系转化为探求面积之间的关系,以直角三角形的各边为边所作的正方形的面积之间有什么关系呢?请你求出图中三个正方形的面积.你是如何得到的?
以BC为边的正方形面积是:
以AC为边的正方形面积是:
以AB为边的正方形面积是:
你是如何得到的?
操作2:在课本第79页的方格纸上,任意画一个顶点都在格点上的直角三角形,并分别以这个直角三角形的各边为一边向三角形外部作正方形,仿照上面的方法计算以斜边为一边的正方形的面积。
结论:面积是边长的平方,面积间的等量关系转化为边长间的等量关系,
即直角三角形三边的等量关系:
用符号语言表述:
∵
∴
3、
拓展导学:
如图,直线l上有三个正方形a、b、c,若a、c的面积为5和11,求b的面积
4、
检测促学:
(1)求下列直角三角形中未知边的长:
(2)求下列图中未知数x、y、z的值:
5、
反思悟学:
这节课你有怎样的收获?还有哪些困惑呢?
苏教版初中数学八年级上册第3章
《勾股定理》教学设计及课堂练习
3.1勾股定理(2)
一、自主先学:
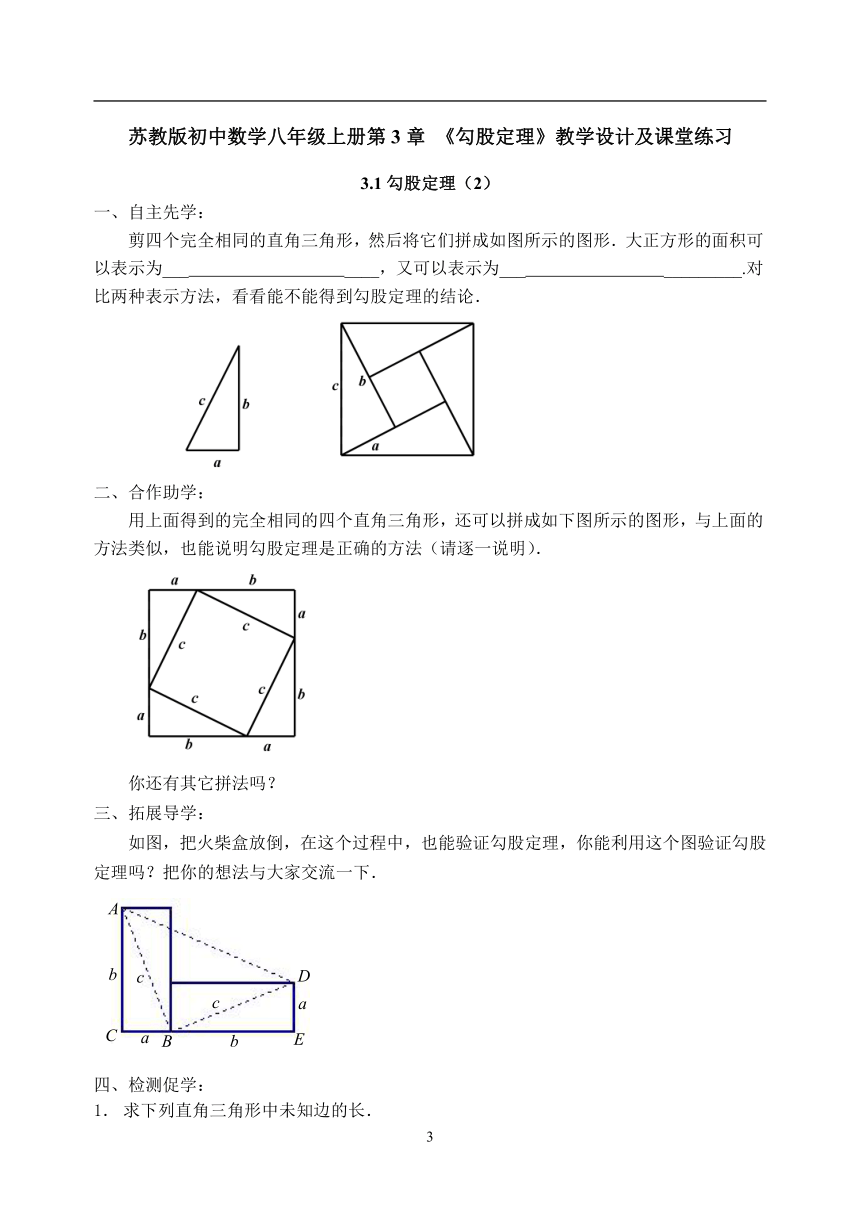
剪四个完全相同的直角三角形,然后将它们拼成如图所示的图形.大正方形的面积可以表示为___
____,又可以表示为___
_________.对比两种表示方法,看看能不能得到勾股定理的结论.
二、合作助学:
用上面得到的完全相同的四个直角三角形,还可以拼成如下图所示的图形,与上面的方法类似,也能说明勾股定理是正确的方法(请逐一说明).
你还有其它拼法吗?
三、拓展导学:
如图,把火柴盒放倒,在这个过程中,也能验证勾股定理,你能利用这个图验证勾股定理吗?把你的想法与大家交流一下.
四、检测促学:
1.
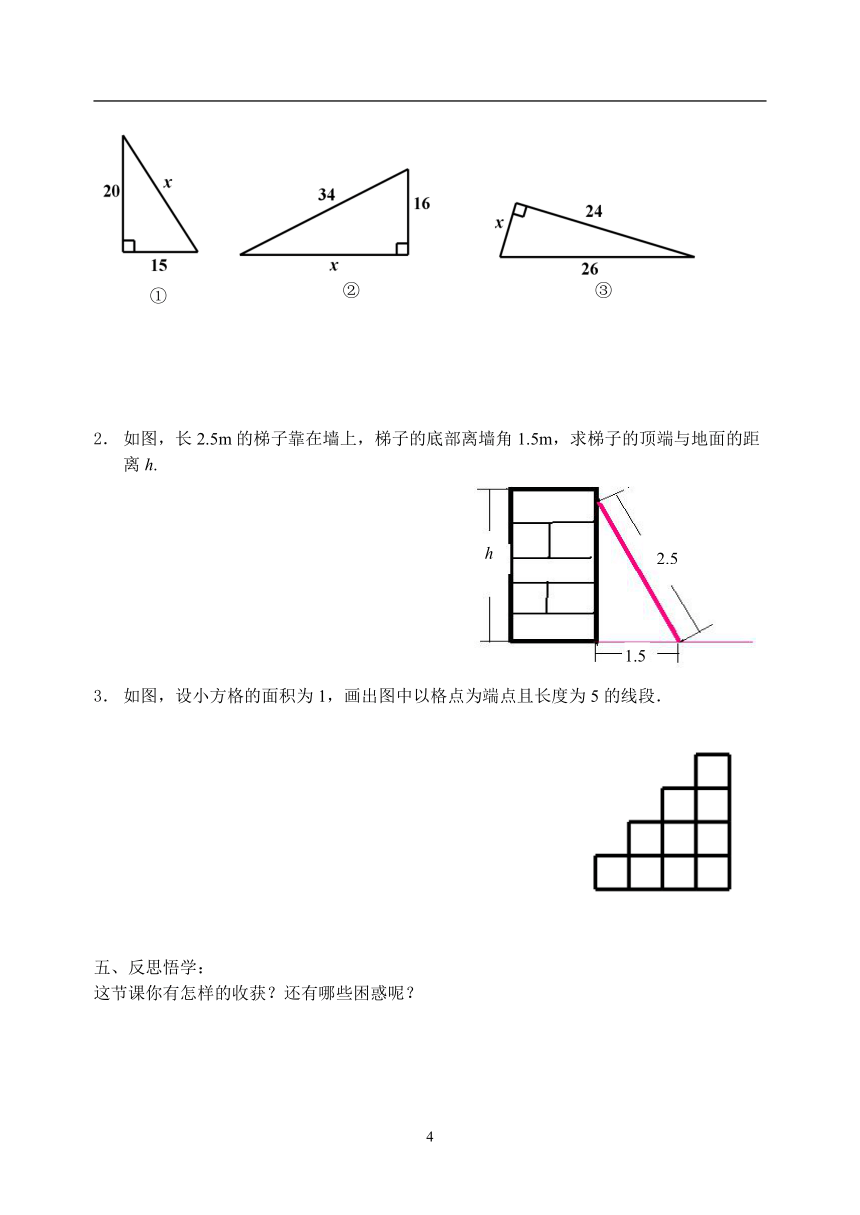
求下列直角三角形中未知边的长.
2.
如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,求梯子的顶端与地面的距离h.
3.
如图,设小方格的面积为1,画出图中以格点为端点且长度为5的线段.
五、反思悟学:
这节课你有怎样的收获?还有哪些困惑呢?
苏教版初中数学八年级上册第3章
《勾股定理》教学设计及课堂练习
3.2勾股定理的逆定理
一、自主先学:
1.画图:画出边长分别是下列各组数的三角形(单位:厘米).
A.3,4,3;??
B.3,4,5;
C.3,4,6;??
D.5,12,13.
2.判断:请判断一下上述你所画的三角形的形状.
3.猜想:三角形的三边满足什么条件时,这个三角形是直角三角形?证明你的猜想.
二、合作助学:
1.通过证明我们得到定理:
用符号语言表述:
∵
∴
2.满足a2+b2=c2的3个正整数a、b、c称为勾股数.
3.除了3、4、5这组勾股数之外,你还能写出其他的勾股数吗?先独立思考,再与同学交流你的结果.
(1)判断:下列各组数是勾股数吗?
①6,8,10;
②9,12,15;
③12,16,20.
你发现什么规律?你还能写出更多的勾股数吗?
三、拓展导学:
已知某校有一块四边形空地ABCD,如图现计划在该空地上种草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需100元,问需投入多少元?
四、检测促学:
1.很久很久以前,古埃及人把一根长绳打上等距离的13个结,然后用桩钉如图那样钉成一个三角形,你知道这个三角形是什么形状吗?并说明理由.
?
2.△ABC的三边长分别是a、b、c,且a
=
n2
-1,b
=
2n,c
=
n2
+1,△ABC是直角三角形吗?证明你的结论.
3.如图,AD⊥BC,垂足为D,如果CD=1,AD=2,BD=4,那么∠BAC是直角吗?证明你的结论.
五、反思悟学:
这节课你有怎样的收获?还有哪些困惑呢?
苏教版初中数学八年级上册第3章
《勾股定理》教学设计及课堂练习
3.3勾股定理的简单应用
1、
自主先学
1.勾股定理:___________________________________________________.
2.甲、乙两人同时从同一地点出发,甲往东走了0.3km,乙往北走了0.4km,这时甲、乙两人相距__________km.
3.如图,从电线杆离地面6
m处向地面拉一条长10
m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有
m.
2、
合作助学
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形.已知桥面以上索塔AB的高,怎样计算AC、AD、AE、AF、AG的长?
3、
拓展导学
1.《九章算术》中的“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?意思是:有一根竹子原高一丈(一丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
2.引葭赴岸”是《九章算术》中另一道题“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”题意是:有一个边长为10尺的正方形池塘,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好到达岸边.请问这个水池的深度和这根芦苇的长度各是多少?
3.如图,等边三角形ABC的边长是6,求△ABC的面积.
4、
检测促学
1.如图,在△ABC中,AB=AC=17,BC=16,求△ABC的面积
2.如图,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积.
五、反思悟学
a
a
b
b
c
c
A
D
E
C
B
①
③
②
h
2.5
1.5
第1题
第2题
第3题
A
C
B
A
C
B
D
A
C
B
D
)7
A
C
B
D
PAGE
49
《勾股定理》教学设计及课堂练习
3.1勾股定理(1)
1、
自主先学:
1.我们已经学过三角形的一些基本知识,如果一个三角形的两条边分别长3和4,你知道第三边的长吗?你知道第三边长的范围吗?
2.如果又已知这两边的夹角是90度,那么第三边的长确定吗?
3.已知直角三角形的两边的长,如何求第三边的长呢?
2、
合作助学:
操作1:运算推演证实我们的猜想:为了计算面积方便,我们可将这将三角形放在方格纸中.如果每一个小方格的边长记作“1”,
我们曾经利用图形面积探索过数学公式,根据经验我们可以将探求边长之间的关系转化为探求面积之间的关系,以直角三角形的各边为边所作的正方形的面积之间有什么关系呢?请你求出图中三个正方形的面积.你是如何得到的?
以BC为边的正方形面积是:
以AC为边的正方形面积是:
以AB为边的正方形面积是:
你是如何得到的?
操作2:在课本第79页的方格纸上,任意画一个顶点都在格点上的直角三角形,并分别以这个直角三角形的各边为一边向三角形外部作正方形,仿照上面的方法计算以斜边为一边的正方形的面积。
结论:面积是边长的平方,面积间的等量关系转化为边长间的等量关系,
即直角三角形三边的等量关系:
用符号语言表述:
∵
∴
3、
拓展导学:
如图,直线l上有三个正方形a、b、c,若a、c的面积为5和11,求b的面积
4、
检测促学:
(1)求下列直角三角形中未知边的长:
(2)求下列图中未知数x、y、z的值:
5、
反思悟学:
这节课你有怎样的收获?还有哪些困惑呢?
苏教版初中数学八年级上册第3章
《勾股定理》教学设计及课堂练习
3.1勾股定理(2)
一、自主先学:
剪四个完全相同的直角三角形,然后将它们拼成如图所示的图形.大正方形的面积可以表示为___
____,又可以表示为___
_________.对比两种表示方法,看看能不能得到勾股定理的结论.
二、合作助学:
用上面得到的完全相同的四个直角三角形,还可以拼成如下图所示的图形,与上面的方法类似,也能说明勾股定理是正确的方法(请逐一说明).
你还有其它拼法吗?
三、拓展导学:
如图,把火柴盒放倒,在这个过程中,也能验证勾股定理,你能利用这个图验证勾股定理吗?把你的想法与大家交流一下.
四、检测促学:
1.
求下列直角三角形中未知边的长.
2.
如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,求梯子的顶端与地面的距离h.
3.
如图,设小方格的面积为1,画出图中以格点为端点且长度为5的线段.
五、反思悟学:
这节课你有怎样的收获?还有哪些困惑呢?
苏教版初中数学八年级上册第3章
《勾股定理》教学设计及课堂练习
3.2勾股定理的逆定理
一、自主先学:
1.画图:画出边长分别是下列各组数的三角形(单位:厘米).
A.3,4,3;??
B.3,4,5;
C.3,4,6;??
D.5,12,13.
2.判断:请判断一下上述你所画的三角形的形状.
3.猜想:三角形的三边满足什么条件时,这个三角形是直角三角形?证明你的猜想.
二、合作助学:
1.通过证明我们得到定理:
用符号语言表述:
∵
∴
2.满足a2+b2=c2的3个正整数a、b、c称为勾股数.
3.除了3、4、5这组勾股数之外,你还能写出其他的勾股数吗?先独立思考,再与同学交流你的结果.
(1)判断:下列各组数是勾股数吗?
①6,8,10;
②9,12,15;
③12,16,20.
你发现什么规律?你还能写出更多的勾股数吗?
三、拓展导学:
已知某校有一块四边形空地ABCD,如图现计划在该空地上种草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需100元,问需投入多少元?
四、检测促学:
1.很久很久以前,古埃及人把一根长绳打上等距离的13个结,然后用桩钉如图那样钉成一个三角形,你知道这个三角形是什么形状吗?并说明理由.
?
2.△ABC的三边长分别是a、b、c,且a
=
n2
-1,b
=
2n,c
=
n2
+1,△ABC是直角三角形吗?证明你的结论.
3.如图,AD⊥BC,垂足为D,如果CD=1,AD=2,BD=4,那么∠BAC是直角吗?证明你的结论.
五、反思悟学:
这节课你有怎样的收获?还有哪些困惑呢?
苏教版初中数学八年级上册第3章
《勾股定理》教学设计及课堂练习
3.3勾股定理的简单应用
1、
自主先学
1.勾股定理:___________________________________________________.
2.甲、乙两人同时从同一地点出发,甲往东走了0.3km,乙往北走了0.4km,这时甲、乙两人相距__________km.
3.如图,从电线杆离地面6
m处向地面拉一条长10
m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有
m.
2、
合作助学
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形.已知桥面以上索塔AB的高,怎样计算AC、AD、AE、AF、AG的长?
3、
拓展导学
1.《九章算术》中的“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?意思是:有一根竹子原高一丈(一丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
2.引葭赴岸”是《九章算术》中另一道题“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”题意是:有一个边长为10尺的正方形池塘,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好到达岸边.请问这个水池的深度和这根芦苇的长度各是多少?
3.如图,等边三角形ABC的边长是6,求△ABC的面积.
4、
检测促学
1.如图,在△ABC中,AB=AC=17,BC=16,求△ABC的面积
2.如图,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积.
五、反思悟学
a
a
b
b
c
c
A
D
E
C
B
①
③
②
h
2.5
1.5
第1题
第2题
第3题
A
C
B
A
C
B
D
A
C
B
D
)7
A
C
B
D
PAGE
49
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
