江苏省高邮一中2021届高三上学期第二次学情检测数学试题 Word版含答案
文档属性
| 名称 | 江苏省高邮一中2021届高三上学期第二次学情检测数学试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 934.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览




文档简介
高邮一中2021届高三上学期第二次学情检测
数学
2020.10
(考试时间:120分钟 试卷满分:150分)
一.单项选择题:本题共8小题,每小题5分,共40分。在每一小题给出的四个选项中,只有一项是正确的,请把正确的选项涂在答题卡相应的位置上。
1.已知集合,则 ( )
A. B. C. D.
2.已知,,,则下列结论正确的是 ( )
A. B. C. D.
3.已知,则的最小值是 ( )
A. B. C. 5 D. 4
4.函数在区间上的图象的大致形状是 ( )
A. B. C. D.
5.已知定义在R上的函数满足,且的图象关于点对称,当时,则 ( )
A. -4 B. 4 C. -5 D. 5
6.已知,则的近似值为 ( )
A. 1.77 B. 1.78 C. 1.79 D. 1.81
7.已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,P是腰DC上的动点,则|+3|的最小值为 ( )
A. -4 B. 5 C. -5 D. 4
8.如图所示,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则(+)·的最小值为 ( )
A. - B. 4 C. -5 D. 5
二.多项选择题:本题共4小题,每小题5分,共20分。在每一小题给出的四个选项中,有多项符合要求,全部选对得5分,部分选对得3分,不选或有选错的得0分。
9.下列有关命题的说法正确的是 ( )
A. ,使得成立
B. 命题,都有,则,使得
C. 函数与函数是同一个函数
D. 若、、均为正实数,且,,则
10.已知曲线C1:y=2sinx,C2:,则 ( )
A.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平行移动个单位长度,
得到曲线C2
B.把C1上各点的横坐标缩短到原来的倍,级坐标不变,再把得到的曲线向右平行移动个单位长度,得到曲线C2
C.把C1向左平行移动个单位长度,再把得到的曲线上各点的横坐标缩短到原来的 倍,纵坐标不变,得到曲线C2
D.把C1向左平行移动个单位长度,再把得到的曲线上各点的横坐标缩短到原来的 倍,纵坐标不变,得到曲线C2
11.若函数对a,bR,同时满足:(1)当a+b=0时有;(2)当a+b>0时
有,则称为函数.下列函数中是函数的有 ( )
A. B. C. D.
12. 设函数若实数,,满足,且.则下列结论恒成立的是 ( )
三.填空题:本题共4小题,每小题5分,共20分。请把答案写在答题卡相应的位置。
13.设函数,若,则实数的取值范围是_________.
14.设为锐角,若,则的值为_________.
15.的内角的对边分别为已知则_________;
若,的面积为,则的周长为_________.
16.已知方程有4个不同的根,则实数的取值范围是_________.
四.解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本题10分)在中,已知,.
(1)求的值;
(2)若,为的中点,求的长.
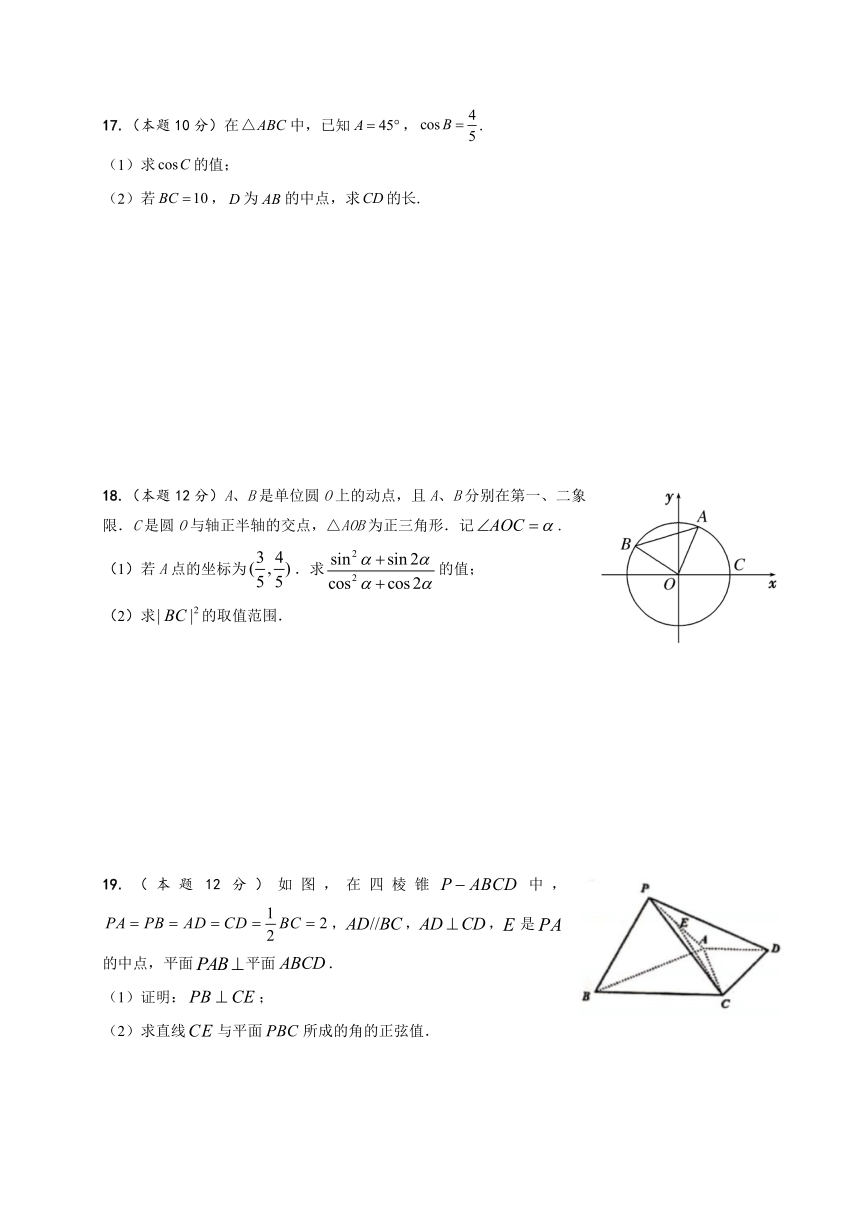
18.(本题12分)A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与轴正半轴的交点,△AOB为正三角形.记.
(1)若A点的坐标为.求的值;
(2)求的取值范围.
19.(本题12分)如图,在四棱锥中,,,,是的中点,平面平面.
(1)证明:;
(2)求直线与平面所成的角的正弦值.
20.(本题12分)将函数的图象向左平移个单位长度后
得到的图象.
(1)若为偶函数,,求的取值范围.
(2)若在上是单调函数,求的取值范围.
21.(本题12分)某医疗机构,为了研究某种病毒在人群中的传播特征,需要检测血液是否为阳性.若现有份血液样本,每份样本被取到的可能性相同,检测方式有以下两种:
方式一:逐份检测,需检测次;
方式二:混合检测,将其中份血液样本分别取样混合在一起检测,若检测结果为阴性,说明这份样本全为阴性,则只需检测1次;若检测结果为阳性,则需要对这份样本逐份检测,因此检测总次数为次.假设每份样本被检测为阳性或阴性是相互独立的,且每份样本为阳性的概率是.
(1)在某地区,通过随机检测发现该地区人群血液为阳性的概率约为.为了调查某单位该病毒感染情况,随机选取人进行检测,有两个分组方案:
方案一:将人分成组,每组人;
方案二:将人分成组,每组人.
试分析哪种方案的检测总次数更少?(取)
(2)现取其中份血液样本,若采用逐份检验方式,需要检测的总次数为;采用混合检测方式,需要检测的总次数为.若,试解决以下问题:
①确定关于的函数关系;
②当为何值时,取最大值并求出最大值.
22.(本题12分)已知函数
(1)讨论的单调性.
(2)若存在两个极值点,,证明:.
2021届高三数学第二次学情检测试卷
参考答案
2020.10
(考试时间:120分钟 试卷满分:150分)
一.单项选择题:
1.C 2.B 3.A 4.A 5.C 6.B 7.B 8.A
二.多项选择题:
9.B D 10.ABC 11.BC 12.ABC
三.填空题:
13.(-∞,0)∪(e,+∞) 14. 15.,。 16.
四.解答题:
17.【解析】(1),且,∴.
.…………………5分
(2)由(1)可得.
由正弦定理得,即,解得.
在中,,,
所以.…………………………………………………………10分
18.解:(1)∵A点的坐标为(,),∴tanα=,
∴=====20.…………5分
(2)设A点的坐标为(x,y),∵△AOB为正三角形,
∴B点的坐标为(cos(α+),sin(α+)),且C(1,0),
∴|BC|2=[cos(α+)-1]2+sin2(α+)=2-2cos(α+).
而A、B分别在第一、二象限,∴α∈(,). ∴α+∈(,),
∴cos(α+)∈(-,0). ∴|BC|2的取值范围是(2,2+).……………………………………………12分
19.(Ⅰ)由已知可得在直角梯形中,,,
所以,所以
又因为平面平面,平面平面
所以平面,所以
又,,所以,所以
故平面,又平面,所以.…………5分
(Ⅱ)由(1)得平面,所以平面平面
所以直线在平面中的射影为直线,
故即为直线与平面所成的角
中,,,,
所以,故
即直线与平面所成的角的正弦值为……………………………………………12分
20.解:(1)
∴
又为偶函数,则,∵,∴
∴
∵,∴
又,∴的取值范围为.…………………6分
(2)∵,∴
∵,∴,
∵在上是单调函数,∴∴..…………………12分
21.解:(1)设方案一中每组的检验次数为,则的取值为
则
则的分布列为:
则,
故方案一的检验总次数的期望为; .…………………3分
设方案二中每组的检验次数为,则的取值为
则.
则的分布列为
则,
故方案二的检验总次数的期望为
因为,则方案二的检测次数更少. .…………………6分
(2)法1:由已知得,则
则
因为,则即…………9分
令,
,
当时,
令,
当时,则在单调递增,
则当时,即,
即当时,,
则………即当时,最大值,
最大值为 …………12分
法2:由已知得,
则,
则,
因为,则,
即,
令,令,
,令得,
当时,,则在上单调递减;
当时,,则在上单调递增;
又因为,则,则的最小值为或,
,
则当即时,最小值,
此时最大即为
22.(1)解:,.
设,
当时,,,则,在上单调递增
当时,,的零点为,,
所以在,上单调递增
在上单调递减
当时,,的零点为,
在上单调递增,在上单调递减.…………5分
(2)证明;由(1)知,当时,存在两个极值点
不妨假设,则
要证,只需证
只需证
即证,
设,设函数,,
因为,所以,,
所以在上单调递减,则
又,则,则
从而…………………………………………………………………………12分
数学
2020.10
(考试时间:120分钟 试卷满分:150分)
一.单项选择题:本题共8小题,每小题5分,共40分。在每一小题给出的四个选项中,只有一项是正确的,请把正确的选项涂在答题卡相应的位置上。
1.已知集合,则 ( )
A. B. C. D.
2.已知,,,则下列结论正确的是 ( )
A. B. C. D.
3.已知,则的最小值是 ( )
A. B. C. 5 D. 4
4.函数在区间上的图象的大致形状是 ( )
A. B. C. D.
5.已知定义在R上的函数满足,且的图象关于点对称,当时,则 ( )
A. -4 B. 4 C. -5 D. 5
6.已知,则的近似值为 ( )
A. 1.77 B. 1.78 C. 1.79 D. 1.81
7.已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,P是腰DC上的动点,则|+3|的最小值为 ( )
A. -4 B. 5 C. -5 D. 4
8.如图所示,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则(+)·的最小值为 ( )
A. - B. 4 C. -5 D. 5
二.多项选择题:本题共4小题,每小题5分,共20分。在每一小题给出的四个选项中,有多项符合要求,全部选对得5分,部分选对得3分,不选或有选错的得0分。
9.下列有关命题的说法正确的是 ( )
A. ,使得成立
B. 命题,都有,则,使得
C. 函数与函数是同一个函数
D. 若、、均为正实数,且,,则
10.已知曲线C1:y=2sinx,C2:,则 ( )
A.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平行移动个单位长度,
得到曲线C2
B.把C1上各点的横坐标缩短到原来的倍,级坐标不变,再把得到的曲线向右平行移动个单位长度,得到曲线C2
C.把C1向左平行移动个单位长度,再把得到的曲线上各点的横坐标缩短到原来的 倍,纵坐标不变,得到曲线C2
D.把C1向左平行移动个单位长度,再把得到的曲线上各点的横坐标缩短到原来的 倍,纵坐标不变,得到曲线C2
11.若函数对a,bR,同时满足:(1)当a+b=0时有;(2)当a+b>0时
有,则称为函数.下列函数中是函数的有 ( )
A. B. C. D.
12. 设函数若实数,,满足,且.则下列结论恒成立的是 ( )
三.填空题:本题共4小题,每小题5分,共20分。请把答案写在答题卡相应的位置。
13.设函数,若,则实数的取值范围是_________.
14.设为锐角,若,则的值为_________.
15.的内角的对边分别为已知则_________;
若,的面积为,则的周长为_________.
16.已知方程有4个不同的根,则实数的取值范围是_________.
四.解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本题10分)在中,已知,.
(1)求的值;
(2)若,为的中点,求的长.
18.(本题12分)A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与轴正半轴的交点,△AOB为正三角形.记.
(1)若A点的坐标为.求的值;
(2)求的取值范围.
19.(本题12分)如图,在四棱锥中,,,,是的中点,平面平面.
(1)证明:;
(2)求直线与平面所成的角的正弦值.
20.(本题12分)将函数的图象向左平移个单位长度后
得到的图象.
(1)若为偶函数,,求的取值范围.
(2)若在上是单调函数,求的取值范围.
21.(本题12分)某医疗机构,为了研究某种病毒在人群中的传播特征,需要检测血液是否为阳性.若现有份血液样本,每份样本被取到的可能性相同,检测方式有以下两种:
方式一:逐份检测,需检测次;
方式二:混合检测,将其中份血液样本分别取样混合在一起检测,若检测结果为阴性,说明这份样本全为阴性,则只需检测1次;若检测结果为阳性,则需要对这份样本逐份检测,因此检测总次数为次.假设每份样本被检测为阳性或阴性是相互独立的,且每份样本为阳性的概率是.
(1)在某地区,通过随机检测发现该地区人群血液为阳性的概率约为.为了调查某单位该病毒感染情况,随机选取人进行检测,有两个分组方案:
方案一:将人分成组,每组人;
方案二:将人分成组,每组人.
试分析哪种方案的检测总次数更少?(取)
(2)现取其中份血液样本,若采用逐份检验方式,需要检测的总次数为;采用混合检测方式,需要检测的总次数为.若,试解决以下问题:
①确定关于的函数关系;
②当为何值时,取最大值并求出最大值.
22.(本题12分)已知函数
(1)讨论的单调性.
(2)若存在两个极值点,,证明:.
2021届高三数学第二次学情检测试卷
参考答案
2020.10
(考试时间:120分钟 试卷满分:150分)
一.单项选择题:
1.C 2.B 3.A 4.A 5.C 6.B 7.B 8.A
二.多项选择题:
9.B D 10.ABC 11.BC 12.ABC
三.填空题:
13.(-∞,0)∪(e,+∞) 14. 15.,。 16.
四.解答题:
17.【解析】(1),且,∴.
.…………………5分
(2)由(1)可得.
由正弦定理得,即,解得.
在中,,,
所以.…………………………………………………………10分
18.解:(1)∵A点的坐标为(,),∴tanα=,
∴=====20.…………5分
(2)设A点的坐标为(x,y),∵△AOB为正三角形,
∴B点的坐标为(cos(α+),sin(α+)),且C(1,0),
∴|BC|2=[cos(α+)-1]2+sin2(α+)=2-2cos(α+).
而A、B分别在第一、二象限,∴α∈(,). ∴α+∈(,),
∴cos(α+)∈(-,0). ∴|BC|2的取值范围是(2,2+).……………………………………………12分
19.(Ⅰ)由已知可得在直角梯形中,,,
所以,所以
又因为平面平面,平面平面
所以平面,所以
又,,所以,所以
故平面,又平面,所以.…………5分
(Ⅱ)由(1)得平面,所以平面平面
所以直线在平面中的射影为直线,
故即为直线与平面所成的角
中,,,,
所以,故
即直线与平面所成的角的正弦值为……………………………………………12分
20.解:(1)
∴
又为偶函数,则,∵,∴
∴
∵,∴
又,∴的取值范围为.…………………6分
(2)∵,∴
∵,∴,
∵在上是单调函数,∴∴..…………………12分
21.解:(1)设方案一中每组的检验次数为,则的取值为
则
则的分布列为:
则,
故方案一的检验总次数的期望为; .…………………3分
设方案二中每组的检验次数为,则的取值为
则.
则的分布列为
则,
故方案二的检验总次数的期望为
因为,则方案二的检测次数更少. .…………………6分
(2)法1:由已知得,则
则
因为,则即…………9分
令,
,
当时,
令,
当时,则在单调递增,
则当时,即,
即当时,,
则………即当时,最大值,
最大值为 …………12分
法2:由已知得,
则,
则,
因为,则,
即,
令,令,
,令得,
当时,,则在上单调递减;
当时,,则在上单调递增;
又因为,则,则的最小值为或,
,
则当即时,最小值,
此时最大即为
22.(1)解:,.
设,
当时,,,则,在上单调递增
当时,,的零点为,,
所以在,上单调递增
在上单调递减
当时,,的零点为,
在上单调递增,在上单调递减.…………5分
(2)证明;由(1)知,当时,存在两个极值点
不妨假设,则
要证,只需证
只需证
即证,
设,设函数,,
因为,所以,,
所以在上单调递减,则
又,则,则
从而…………………………………………………………………………12分
同课章节目录
