函数y=asin(ωx+φ)的图象
文档属性
| 名称 | 函数y=asin(ωx+φ)的图象 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-08 00:00:00 | ||
图片预览

文档简介
1 几何画板5.03制作,用自带程序打开
2 用NOD32扫描过,无病毒.课件:y=Asin( x+ 设计和操作说明
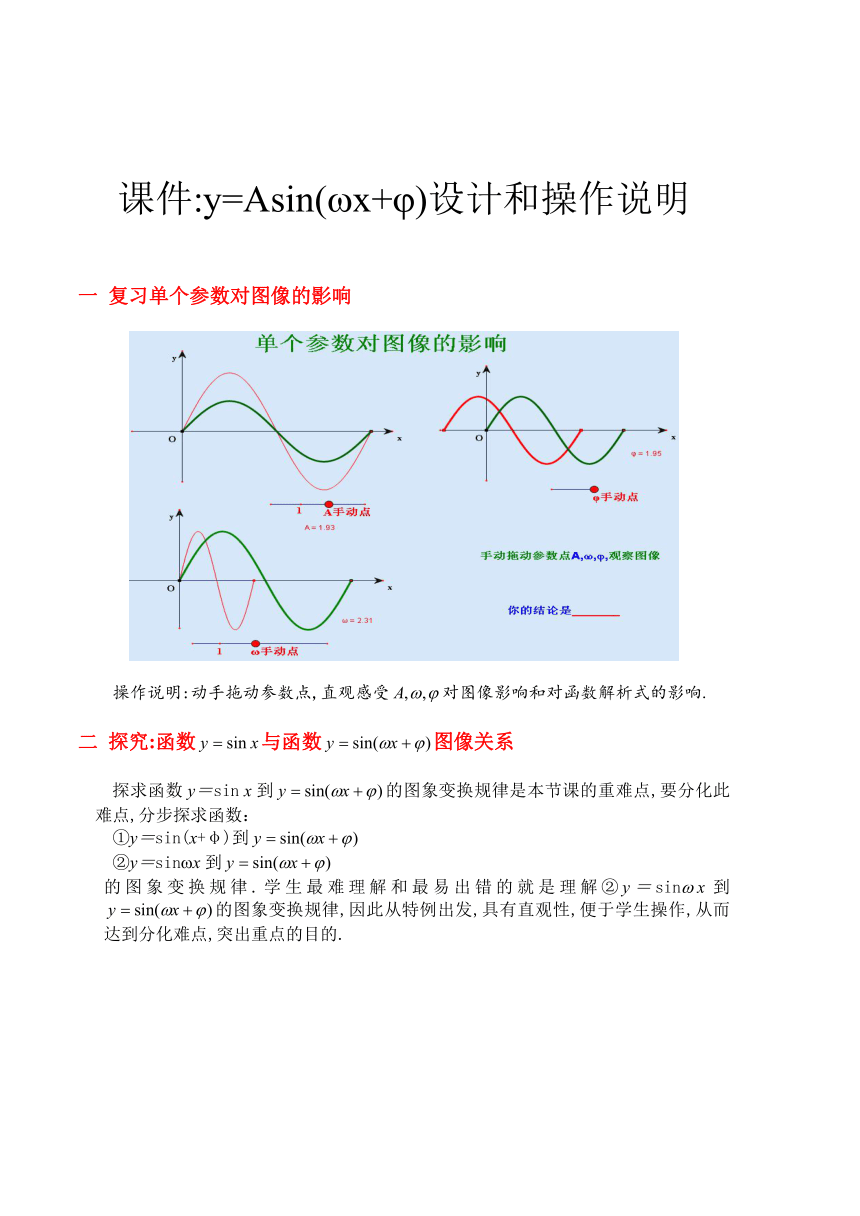
一 复习单个参数对图像的影响
操作说明:动手拖动参数点,直观感受对图像影响和对函数解析式的影响.
二 探究:函数与函数图像关系
探求函数y=sin x到的图象变换规律是本节课的重难点,要分化此难点,分步探求函数:
①y=sin(x+φ)到
②y=sin x到
的图象变换规律.学生最难理解和最易出错的就是理解②y=sin x到的图象变换规律,因此从特例出发,具有直观性,便于学生操作,从而达到分化难点,突出重点的目的.
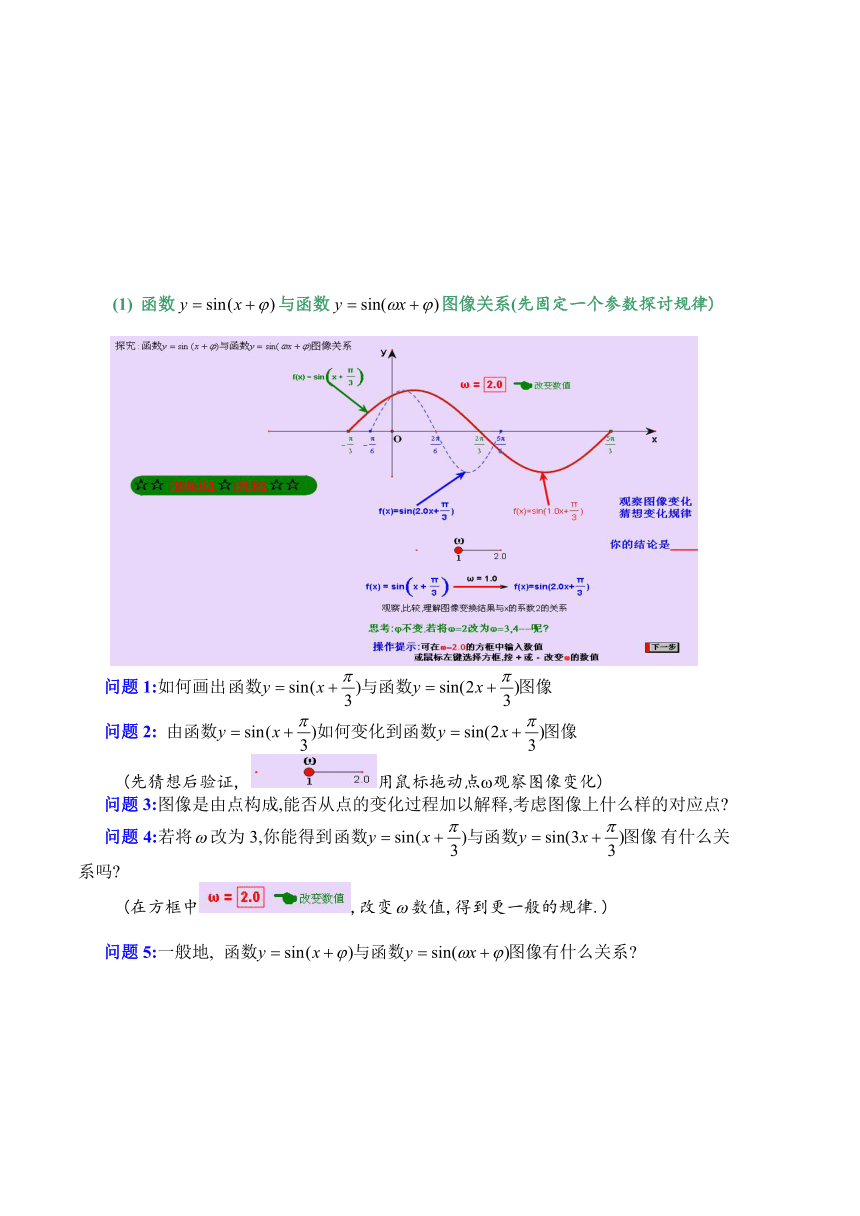
函数与函数图像关系(先固定一个参数探讨规律)
问题1:如何画出
问题2:
(先猜想后验证, 用鼠标拖动点 观察图像变化)
问题3:图像是由点构成,能否从点的变化过程加以解释,考虑图像上什么样的对应点
问题4:若将改为3,你能得到有什么关系吗
(在方框中,改变数值,得到更一般的规律.)
问题5:一般地,
函数与函数图像关系
问题1:如何画出
问题2:
(,拖动 点观察图像的平移量)
问题3:能否结合点的变化来思考函数图像变化,此时,又该考虑两个图像上什么样对应点
问题4:若将改为3,你能得到有什么关系吗
(,在方框中改变数值后再观察,得到更一般的规律)
问题5:一般地,
(3) 函数与函数图像关系
通过实例综合以上两种变换,重点是比较两种方法平移量的区别和导致这一现象的根本原因,并由此导出一般规律
问题1:如何由
(得到两种变换途径,但要注意两者的平移量会有不同,结合零点解释)
问题2:一般地,
三: 探究:函数与函数图像关系
前面问题解决的基础上,体会振幅A的位置对ω和φ无影响,得到两种变换途径一般性规律.
(1) 思考:y=sinx图像变化得到y=3sin(2x+)图像
(在(二)的基础上, ,拖动按钮A放入左边两种变换中所对应的位置,感受A的先后顺序对另两个参数无影响)
(2) 思考:由y=图像变化得到y=图像
操作说明:先确定三个对数的值,在方框中输入具体的数值
在对应的变换途径下,从上到下拖动参数点观察图像变化.
2 用NOD32扫描过,无病毒.课件:y=Asin( x+ 设计和操作说明
一 复习单个参数对图像的影响
操作说明:动手拖动参数点,直观感受对图像影响和对函数解析式的影响.
二 探究:函数与函数图像关系
探求函数y=sin x到的图象变换规律是本节课的重难点,要分化此难点,分步探求函数:
①y=sin(x+φ)到
②y=sin x到
的图象变换规律.学生最难理解和最易出错的就是理解②y=sin x到的图象变换规律,因此从特例出发,具有直观性,便于学生操作,从而达到分化难点,突出重点的目的.
函数与函数图像关系(先固定一个参数探讨规律)
问题1:如何画出
问题2:
(先猜想后验证, 用鼠标拖动点 观察图像变化)
问题3:图像是由点构成,能否从点的变化过程加以解释,考虑图像上什么样的对应点
问题4:若将改为3,你能得到有什么关系吗
(在方框中,改变数值,得到更一般的规律.)
问题5:一般地,
函数与函数图像关系
问题1:如何画出
问题2:
(,拖动 点观察图像的平移量)
问题3:能否结合点的变化来思考函数图像变化,此时,又该考虑两个图像上什么样对应点
问题4:若将改为3,你能得到有什么关系吗
(,在方框中改变数值后再观察,得到更一般的规律)
问题5:一般地,
(3) 函数与函数图像关系
通过实例综合以上两种变换,重点是比较两种方法平移量的区别和导致这一现象的根本原因,并由此导出一般规律
问题1:如何由
(得到两种变换途径,但要注意两者的平移量会有不同,结合零点解释)
问题2:一般地,
三: 探究:函数与函数图像关系
前面问题解决的基础上,体会振幅A的位置对ω和φ无影响,得到两种变换途径一般性规律.
(1) 思考:y=sinx图像变化得到y=3sin(2x+)图像
(在(二)的基础上, ,拖动按钮A放入左边两种变换中所对应的位置,感受A的先后顺序对另两个参数无影响)
(2) 思考:由y=图像变化得到y=图像
操作说明:先确定三个对数的值,在方框中输入具体的数值
在对应的变换途径下,从上到下拖动参数点观察图像变化.
