人教高中数学必修三3.2.1古典概型 说课课件(39张ppt)
文档属性
| 名称 | 人教高中数学必修三3.2.1古典概型 说课课件(39张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 595.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览









文档简介
(共39张PPT)
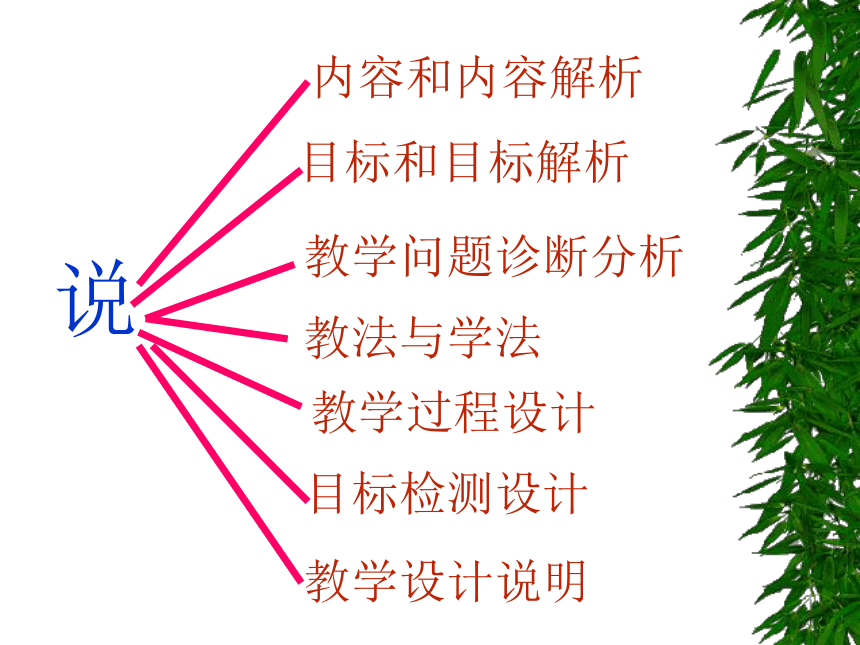
说
内容和内容解析
目标和目标解析
教学问题诊断分析
教法与学法
教学过程设计
教学设计说明
目标检测设计
本节课是高中数学(必修)
3第三章概率的第二节古典概型的第一课时,是在随机事件的概率之后,几何概型之前,并且在尚未学习排列组合的情况下安排的。前面学习的随机事件概率的求法是通过大量重复试验用频率来估计,而古典概型的概率计算,避免了大量的重复试验,可通过分析结果来计算,而且得到的是概率的精确值,这是相对于随机事件的一大进步。同时古典概型也是后面学习条件概率的基础,起到承前启后的作用,所以在概率论中占有相当重要的地位。
一.内容和内容解析
主要内容有:
1.基本事件的概念及特点,
2.古典概型的概念及特征,
3.古典概型的概率计算公式。
二.目标和目标解析
1.了解基本事件的概念和特点。
2.理解古典概型及其概率计算公式。
3.会用列举法计算一些随机事件所含的基本事件数及事件发生的概率。
4.会初步应用概率计算公式解决简单的古典概型问题。
三.教学问题诊断分析
学生虽然有了一些概率的知识储备,但因为学生尚未学习排列组合的知识,所以学习依然有困难。
本节课的重点是理解古典概型的概念及利用古典概型公式求随机事件的概率。
本节课的教学难点是如何判断一个试验是否是古典概型,分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数。
教学中,我准备从一开始就采用问题串的形式激发学生质疑,让同学们随时带着问题自主探究、合作交流,充分体现生本教育和新课程的理念。
四.教法学法
问题1:考察两个试验:
(1)抛掷一枚质地均匀的硬币的试验;
(2)掷一颗质地均匀的骰子的试验。在这两个试验中,可能的结果分别有哪些?
问题2:基本事件有什么特点?
五.教学过程设计
(一)创设情境,引出课题
设计意图:通过掷硬币与掷骰子两个实际生活中的试验,激发学生的学习兴趣,让学生观察试验,分析结果,找出共性,最终目的是让同学们自己总结出基本事件的特点。
五.教学过程设计
(一)创设情境,引出课题
问题3:在掷骰子试验中,随机试验“出现偶数点”可以由哪些基本事件组成?
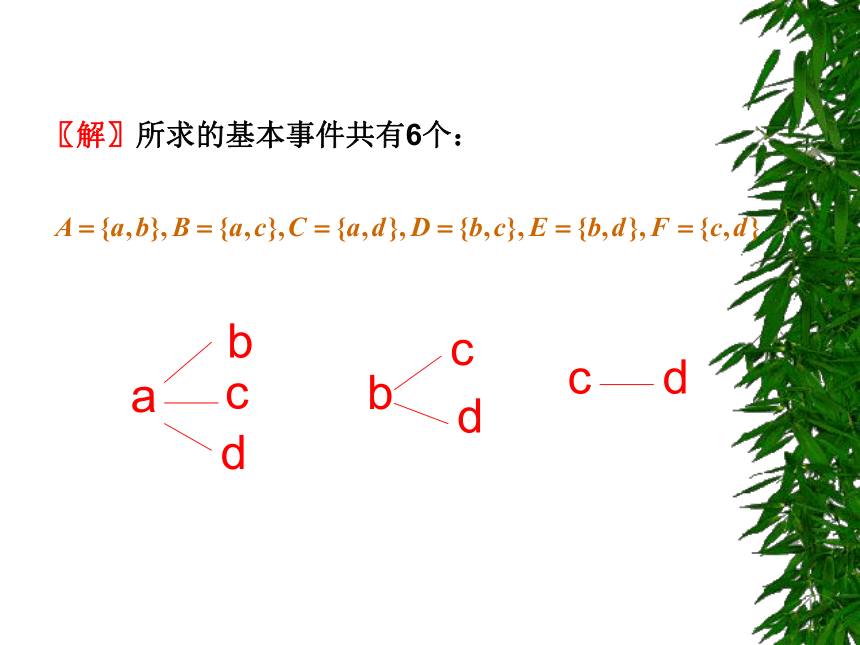
问题4:从字母a,b,c,d中任意取出两个不同字母的实验中,有那些基本事件?
五.教学过程设计
(一)创设情境,引出课题
b
c
d
b
c
d
a
c
d
〖解〗所求的基本事件共有6个:
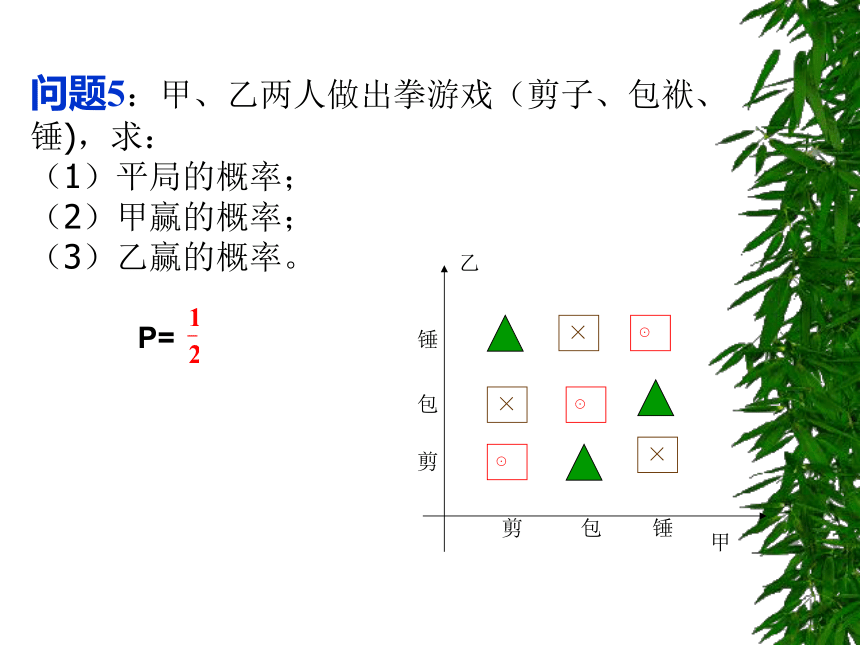
问题5:甲、乙两人做出拳游戏(剪子、包袱、锤),求:
(1)平局的概率;
(2)甲赢的概率;
(3)乙赢的概率。
乙
甲
⊙
×
剪
包
锤
剪
包
锤
×
⊙
×
⊙
P=
设计意图:
设计问题3是为了加深对基本事件的理解。
设计问题4是为了让同学们会用树形图来列举基本事件的个数,将数形结合和分类讨论的思想渗透到具体问题中来,显得更形象直观,并且避免重复和遗漏。
问题5是同学们比较熟悉的生活问题,运用图形列举清晰明了。
以上三个问题的设计是为了突破求古典概型中基本事件总数这一难点。
.
问题6:你知道掷均匀硬币出现正面朝上的概率是多少?掷骰子出现偶数点的概率是多少?例1中出现字母“d”的概率又是多少?
五.教学过程设计
(二)通过设疑,引出概念
问题7:上述概率公式的推导过程中基本事件有什么特点?
设计意图:对问题6,学生根据已有的知识,已经可以独立得出概率,在教师的步步追问下,再探讨问题,目的是为了得出概率公式。
得出概率公式后,设计问题7,目的是为了培养学生观察和概括归纳的能力。通过问题的解决引出古典概型的概念。
问题8:
(1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的。
(2)某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环。
(3)从五位学生中随机地选择两位去参加一项集体活动。
(4)向一个方格随机地投一个石子,如果该石子落在方格内任意一点都是等可能的。
(5)某一同学把面包上抹上果酱来模拟硬币落地的情况,结果抹果酱的一面着地。以上事件是否为古典概型?为什么?
(1)、(4)不是古典概型,因为试验的所有可能结果是圆面(方格)内所有的点,试验的所有可能结果数是无限的;(2)不是古典概型,因为试验的所有可能结果只有7个,而命中10环、命中9环……命中5环和不中环的出现不是等可能的,即不满足古典概型的第二个条件。(3)是古典概型。(5)不是古典概型,因为果酱两面着地不是等可能的,即不满足古典概型的第二个条件。
设计意图:几个问题的设计是为了让学生更加准确的把握古典概型的两个特点。目的是突破如何判断一个试验是否是古典概型这一教学难点。
.
问题9:
单选题是标准化考试中常用的题型,一般是从A、B、C、D四个选项中选择一个正确答案。如果考生掌握了考察内容,他可以选择唯一正确的答案。假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
五.教学过程设计
(三)例题分析,加深理解
设计意图:这节课的难点就是古典概型的判断,设计问题9目的就是为了
突破难点。
本题中,要向同学们讲清,假设考生不会做,他随机的选择一个答案,满足古典概型的等可能性,又因为只有四个答案,满足古典概型的有限性。
如果考生掌握或者掌握了部分考察内容,这都不满足古典概型的第2个条件——等可能性,因此,只有在假定考生不会做,随机地选择了一个答案的情况下,才可以化为古典概型。
由此掌握求此类题目的方法,让学生进一步理解古典概型的概率计算公式,体验概率与实际生活是息息相关的。
问题10:在标准化的考试中既有单选题又有多选题,多选题是从A、B、C、D四个选项中选择所有正确答案,同学们有一种感觉,如果不知道正确答案多选题更难猜对,这是为什么?
问题11:同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?
问题12:把问题4和例11作比较,你能找出它们的联系和区别吗?
设计意图:
设计问题10,目的是引导学生用列举法列举15种可能出现的答案,判断是否满足古典概型的特征,再利用概率公式求值。
设计问题11,目的是引导学生用列表的方法来列举所有可能的情况解决问题。但课前要对课堂上的问题具有预见性。
对于问题11,可能有个别同学可能这样解:
解:(1)
所有结果共有21种,如下所示:
(1,1)
(2,1)
(2,2)
(3,1)
(3,2)
(3,3)
(4,1)
(4,2)
(4,3)
(4,4)
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,3)
(2,4)
(2,5)
(2,6)
(3,4)
(3,5)
(3,6)
(4,5)
(4,6)
(5,6)
(2)其中向上的点数之和是5的结果有2种。
(3)向上的点数之和是5的概率是2/21
正确而又简洁直观解法应当列表如下,课上应当向同学们讲清错误的原因是把(2,3)和(3,2)等看成一样的了,这也正是为什么把两粒骰子作上标号的原因。
问题13:假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,2…,9十个数字中的任意一个。假设一个人完全忘记了密码,问他到自动提款机上随机式一次密码就能取到钱的概率是多少?
五.教学过程设计
(四)循序渐进,例题延伸
问题14
设计意图:选用具有现实意义的例题,激发学生的学习兴趣,培养其运用数学知识解决实际问题的能力。
问题15:一次投掷两颗骰子,求出现的点数之和为奇数的概率。
五.教学过程设计
(五)变式练习,巩固提高
设计意图:为了体现知识的波浪式深入螺旋式上升,设计一题多解的变式练习,有三种解法,体现了数学的多变性和灵活性,进一步开拓学生的发散思维。
第1题:
在夏令营的7名成员中,有3名同学已去过北京。从这7名同学中任选2名同学,选出的这2名同学恰是已去过北京的概率是多少?
六.目标检测设计
第2题:下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,分别计算甲获胜的概率,哪个游戏是公平的??
游戏1
游戏2
游戏3
1个红球和1个白球
2个红球和2个白球
3个红球和1个白球
取1个球
取1个球,再取1个球
取1个球,再取1个球
取出的球是红球→甲胜
取出的两个球同色→甲胜
取出的两个球同色→甲胜
取出的球是白球→乙胜
取出的两个球不同色→乙胜
取出的两个球不同色→乙胜
第3题:某城市的电话号码是8位数,如果从电话号码中任指一个电话号码,求:
(1)头两位数码都是8的概率;
(2)头两位数码至少有一个不超过8的概率;
(3)头两位数码不相同的概率。
设计意图:从实际问题出发,加强前后知识的联系,结合古典概型和概率的性质,计算事件发生的概率,培养学生的对知识的综合运用能力。
1.根据本节课的特点,采用引导发现和归纳概括相结合的教学方法,通过提出问题、思考问题、解决问题等教学过程,观察对比、概括归纳古典概型的概念及其概率公式,再通过具体问题的提出和解决,来激发学生的学习兴趣,调动学生的主体能动性,让每一个学生充分地参与到学习活动中来。
七.教学设计说明
2.学生在教师创设的问题情景中,通过观察、类比、思考、探究、概括、归纳和动手尝试相结合,体现了学生的主体地位,培养了学生由具体到抽象,由特殊到一般的数学思维能力,形成了实事求是的科学态度,增强了锲而不舍的求学精神。
3.以问题为纽带,化结果为过程的教学理念始终贯穿了整个教学过程,因为我们不仅希望学生掌握知识,更希望学生掌握分析知识、选择知识、更新知识的能力。简单的说智慧比知识更重要,知识是启发智慧的手段,过程是结果的动态延伸,教学中能够把结果变成过程,才能把知识变成智慧!
板书设计
古典概型
①
基本概念
………
………
②
古典概型公式
………
………
③
典型例题……
………
………
问题1:
问题2:
问题3:
问题4:
…………
………
……
…………………
………
………
投影屏幕
谢谢各位评委!
说
内容和内容解析
目标和目标解析
教学问题诊断分析
教法与学法
教学过程设计
教学设计说明
目标检测设计
本节课是高中数学(必修)
3第三章概率的第二节古典概型的第一课时,是在随机事件的概率之后,几何概型之前,并且在尚未学习排列组合的情况下安排的。前面学习的随机事件概率的求法是通过大量重复试验用频率来估计,而古典概型的概率计算,避免了大量的重复试验,可通过分析结果来计算,而且得到的是概率的精确值,这是相对于随机事件的一大进步。同时古典概型也是后面学习条件概率的基础,起到承前启后的作用,所以在概率论中占有相当重要的地位。
一.内容和内容解析
主要内容有:
1.基本事件的概念及特点,
2.古典概型的概念及特征,
3.古典概型的概率计算公式。
二.目标和目标解析
1.了解基本事件的概念和特点。
2.理解古典概型及其概率计算公式。
3.会用列举法计算一些随机事件所含的基本事件数及事件发生的概率。
4.会初步应用概率计算公式解决简单的古典概型问题。
三.教学问题诊断分析
学生虽然有了一些概率的知识储备,但因为学生尚未学习排列组合的知识,所以学习依然有困难。
本节课的重点是理解古典概型的概念及利用古典概型公式求随机事件的概率。
本节课的教学难点是如何判断一个试验是否是古典概型,分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数。
教学中,我准备从一开始就采用问题串的形式激发学生质疑,让同学们随时带着问题自主探究、合作交流,充分体现生本教育和新课程的理念。
四.教法学法
问题1:考察两个试验:
(1)抛掷一枚质地均匀的硬币的试验;
(2)掷一颗质地均匀的骰子的试验。在这两个试验中,可能的结果分别有哪些?
问题2:基本事件有什么特点?
五.教学过程设计
(一)创设情境,引出课题
设计意图:通过掷硬币与掷骰子两个实际生活中的试验,激发学生的学习兴趣,让学生观察试验,分析结果,找出共性,最终目的是让同学们自己总结出基本事件的特点。
五.教学过程设计
(一)创设情境,引出课题
问题3:在掷骰子试验中,随机试验“出现偶数点”可以由哪些基本事件组成?
问题4:从字母a,b,c,d中任意取出两个不同字母的实验中,有那些基本事件?
五.教学过程设计
(一)创设情境,引出课题
b
c
d
b
c
d
a
c
d
〖解〗所求的基本事件共有6个:
问题5:甲、乙两人做出拳游戏(剪子、包袱、锤),求:
(1)平局的概率;
(2)甲赢的概率;
(3)乙赢的概率。
乙
甲
⊙
×
剪
包
锤
剪
包
锤
×
⊙
×
⊙
P=
设计意图:
设计问题3是为了加深对基本事件的理解。
设计问题4是为了让同学们会用树形图来列举基本事件的个数,将数形结合和分类讨论的思想渗透到具体问题中来,显得更形象直观,并且避免重复和遗漏。
问题5是同学们比较熟悉的生活问题,运用图形列举清晰明了。
以上三个问题的设计是为了突破求古典概型中基本事件总数这一难点。
.
问题6:你知道掷均匀硬币出现正面朝上的概率是多少?掷骰子出现偶数点的概率是多少?例1中出现字母“d”的概率又是多少?
五.教学过程设计
(二)通过设疑,引出概念
问题7:上述概率公式的推导过程中基本事件有什么特点?
设计意图:对问题6,学生根据已有的知识,已经可以独立得出概率,在教师的步步追问下,再探讨问题,目的是为了得出概率公式。
得出概率公式后,设计问题7,目的是为了培养学生观察和概括归纳的能力。通过问题的解决引出古典概型的概念。
问题8:
(1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的。
(2)某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环。
(3)从五位学生中随机地选择两位去参加一项集体活动。
(4)向一个方格随机地投一个石子,如果该石子落在方格内任意一点都是等可能的。
(5)某一同学把面包上抹上果酱来模拟硬币落地的情况,结果抹果酱的一面着地。以上事件是否为古典概型?为什么?
(1)、(4)不是古典概型,因为试验的所有可能结果是圆面(方格)内所有的点,试验的所有可能结果数是无限的;(2)不是古典概型,因为试验的所有可能结果只有7个,而命中10环、命中9环……命中5环和不中环的出现不是等可能的,即不满足古典概型的第二个条件。(3)是古典概型。(5)不是古典概型,因为果酱两面着地不是等可能的,即不满足古典概型的第二个条件。
设计意图:几个问题的设计是为了让学生更加准确的把握古典概型的两个特点。目的是突破如何判断一个试验是否是古典概型这一教学难点。
.
问题9:
单选题是标准化考试中常用的题型,一般是从A、B、C、D四个选项中选择一个正确答案。如果考生掌握了考察内容,他可以选择唯一正确的答案。假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
五.教学过程设计
(三)例题分析,加深理解
设计意图:这节课的难点就是古典概型的判断,设计问题9目的就是为了
突破难点。
本题中,要向同学们讲清,假设考生不会做,他随机的选择一个答案,满足古典概型的等可能性,又因为只有四个答案,满足古典概型的有限性。
如果考生掌握或者掌握了部分考察内容,这都不满足古典概型的第2个条件——等可能性,因此,只有在假定考生不会做,随机地选择了一个答案的情况下,才可以化为古典概型。
由此掌握求此类题目的方法,让学生进一步理解古典概型的概率计算公式,体验概率与实际生活是息息相关的。
问题10:在标准化的考试中既有单选题又有多选题,多选题是从A、B、C、D四个选项中选择所有正确答案,同学们有一种感觉,如果不知道正确答案多选题更难猜对,这是为什么?
问题11:同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?
问题12:把问题4和例11作比较,你能找出它们的联系和区别吗?
设计意图:
设计问题10,目的是引导学生用列举法列举15种可能出现的答案,判断是否满足古典概型的特征,再利用概率公式求值。
设计问题11,目的是引导学生用列表的方法来列举所有可能的情况解决问题。但课前要对课堂上的问题具有预见性。
对于问题11,可能有个别同学可能这样解:
解:(1)
所有结果共有21种,如下所示:
(1,1)
(2,1)
(2,2)
(3,1)
(3,2)
(3,3)
(4,1)
(4,2)
(4,3)
(4,4)
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,3)
(2,4)
(2,5)
(2,6)
(3,4)
(3,5)
(3,6)
(4,5)
(4,6)
(5,6)
(2)其中向上的点数之和是5的结果有2种。
(3)向上的点数之和是5的概率是2/21
正确而又简洁直观解法应当列表如下,课上应当向同学们讲清错误的原因是把(2,3)和(3,2)等看成一样的了,这也正是为什么把两粒骰子作上标号的原因。
问题13:假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,2…,9十个数字中的任意一个。假设一个人完全忘记了密码,问他到自动提款机上随机式一次密码就能取到钱的概率是多少?
五.教学过程设计
(四)循序渐进,例题延伸
问题14
设计意图:选用具有现实意义的例题,激发学生的学习兴趣,培养其运用数学知识解决实际问题的能力。
问题15:一次投掷两颗骰子,求出现的点数之和为奇数的概率。
五.教学过程设计
(五)变式练习,巩固提高
设计意图:为了体现知识的波浪式深入螺旋式上升,设计一题多解的变式练习,有三种解法,体现了数学的多变性和灵活性,进一步开拓学生的发散思维。
第1题:
在夏令营的7名成员中,有3名同学已去过北京。从这7名同学中任选2名同学,选出的这2名同学恰是已去过北京的概率是多少?
六.目标检测设计
第2题:下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,分别计算甲获胜的概率,哪个游戏是公平的??
游戏1
游戏2
游戏3
1个红球和1个白球
2个红球和2个白球
3个红球和1个白球
取1个球
取1个球,再取1个球
取1个球,再取1个球
取出的球是红球→甲胜
取出的两个球同色→甲胜
取出的两个球同色→甲胜
取出的球是白球→乙胜
取出的两个球不同色→乙胜
取出的两个球不同色→乙胜
第3题:某城市的电话号码是8位数,如果从电话号码中任指一个电话号码,求:
(1)头两位数码都是8的概率;
(2)头两位数码至少有一个不超过8的概率;
(3)头两位数码不相同的概率。
设计意图:从实际问题出发,加强前后知识的联系,结合古典概型和概率的性质,计算事件发生的概率,培养学生的对知识的综合运用能力。
1.根据本节课的特点,采用引导发现和归纳概括相结合的教学方法,通过提出问题、思考问题、解决问题等教学过程,观察对比、概括归纳古典概型的概念及其概率公式,再通过具体问题的提出和解决,来激发学生的学习兴趣,调动学生的主体能动性,让每一个学生充分地参与到学习活动中来。
七.教学设计说明
2.学生在教师创设的问题情景中,通过观察、类比、思考、探究、概括、归纳和动手尝试相结合,体现了学生的主体地位,培养了学生由具体到抽象,由特殊到一般的数学思维能力,形成了实事求是的科学态度,增强了锲而不舍的求学精神。
3.以问题为纽带,化结果为过程的教学理念始终贯穿了整个教学过程,因为我们不仅希望学生掌握知识,更希望学生掌握分析知识、选择知识、更新知识的能力。简单的说智慧比知识更重要,知识是启发智慧的手段,过程是结果的动态延伸,教学中能够把结果变成过程,才能把知识变成智慧!
板书设计
古典概型
①
基本概念
………
………
②
古典概型公式
………
………
③
典型例题……
………
………
问题1:
问题2:
问题3:
问题4:
…………
………
……
…………………
………
………
投影屏幕
谢谢各位评委!
