人教新课标A版必修2 第二章 立体几何大题练习(含解析)
文档属性
| 名称 | 人教新课标A版必修2 第二章 立体几何大题练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 15:22:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
立体几何大题
1.四棱锥中,侧面为等边三角形且垂直于底面
,
(1)证明:直线平面;
(2)若△面积为,求四棱锥的体积.
【解析】(1)
在平面内,因为,所以
又平面平面故平面
(2)取的中点,连接
由及
得四边形为正方形,则.
因为侧面为等边三角形且垂直于底面,平面平面,
所以底面
因为底面,所以,
设,则,取的中点,连接,则,所以,
因为的面积为,所以,
解得(舍去),
于是
所以四棱锥的体积
2.如图,已知四棱锥,侧面是正三角形,底面为边长2的菱形,,.
(1)设平面平面,求证:;
(2)求多面体的体积;
(3)求二面角的余弦值.
【解析】证明:(1)因为平面平面,
所以平面,
又平面,平面平面,所以;
(2)取中点,连结,由得,
同理,又因为,所以平面,
在中,,所以,
所以多面体的体积
;
(3)由题意知,底面为边长2的菱形,,
所以,又,所以
设的中点为,连结,
由侧面是正三角形知,,所以,
因此就是二面角的平面角,
在中,,,
由余弦定理得,
二面角的余弦值为.
3.如图,正方体,棱长为a,E,F分别为、上的点,且.
(1)当x为何值时,三棱锥的体积最大?
(2)求三棱椎的体积最大时,二面角的正切值;
(3)求异面直线与所成的角的取值范围.
【解析】(1)因为正方体,所以平面
所以,
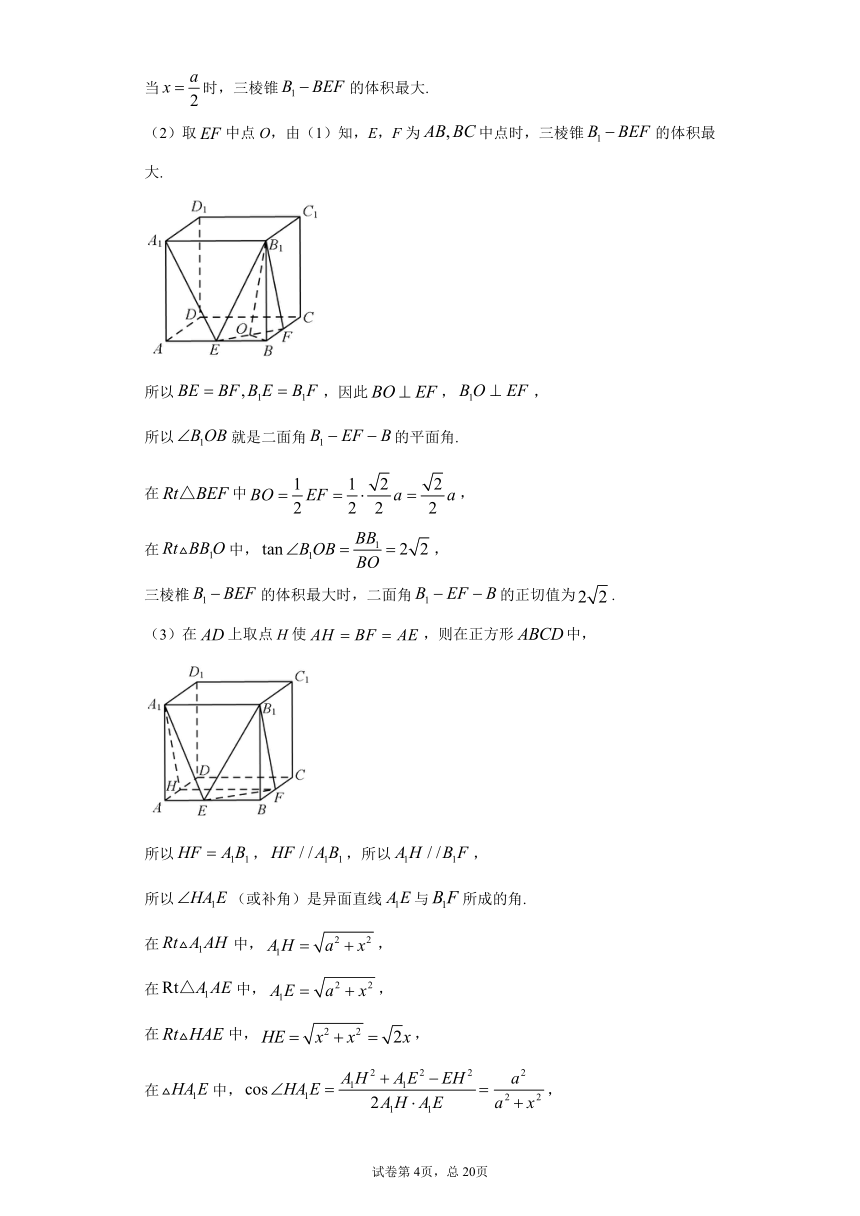
当时,三棱锥的体积最大.
(2)取中点O,由(1)知,E,F为中点时,三棱锥的体积最大.
所以,因此,,
所以就是二面角的平面角.
在中,
在中,,
三棱椎的体积最大时,二面角的正切值为.
(3)在上取点H使,则在正方形中,
所以,,所以,
所以(或补角)是异面直线与所成的角.
在中,,
在中,,
在中,,
在中,,
因为,所以,所以,
所以,所以
所以异面直线与所成的角的取值范围为.
4.如图所示,四棱锥的底面是边长为2的正方形,底面,为的中点.
(1)求证:平面;
(2)求证:平面;
(3)若三棱锥的体积为,求四棱锥的侧面积.
【解析】(1)连结,交于点.连结,
因为四边形是正方形,所以为的中点,
又为的中点,所以为的中位线,所以,
又平面,平面,所以平面.
(2)因为四边形是正方形,所以,
因为底面,所以,
又,所以平面.
(3)因为,
又因为底面是边长为2的正方形,所以,所以,
又因为是的中点,所以.所以,
所以四棱锥的侧面积
.
5.如图,四棱锥中,底面,,,,,是的中点.
(1)求证:;
(2)求证:面;
(3)求二面角E-AB-C的正切值.
【答案】(1)见解析;(2)见解析;(3)
【解析】(1)证明:∵底面,
又,,故面
面,故
(2)证明:,,故
是的中点,故
由(1)知,从而面,故
易知,故面
(3)过点E作EF⊥AC,垂足为.过点F作FG⊥AB,垂足为G.连结EG
∵PA⊥AC,
∴PA//EF
∴EF⊥底面且F是AC中点
∴故是二面角的一个平面角.
设,则PA=BC=,EF=AF=
从而FG=,故.
6.已知三棱锥中,为等腰直角三角形,,,设点为中点,点为中点,点为上一点,且.
(1)证明:平面;
(2)若,求三棱锥的表面积.
【解析】(1)连接交于点,连接,
点为中点,点为中点,点为的重心,,
,,
又平面,平面,平面.
(2)因为,,,
所以全等于,,,,
所以,
在中,,,则边上的高为,
所以,
.
7.如图,三棱柱中,侧面,已知,,,点是棱的中点.
(1)求证:平面;
(2)求与平面所成角的正弦值.
【解析】(1)由题意,因为,,,由余弦定理可得,
因为,所以,
又因为侧面,所以,
又由,平面,
所以直线平面.
(2)在中,且,可得,
又由且,所以.
又因为,则,即,
因为平面,所以平面,则,
又由平面,平面且,则,
则为所求与平面所成角,
在直角中,所以.
8.如图,在正三棱柱中,底面边长为2,为的中点,三棱柱的体积.
(1)求三棱柱的表面积;
(2)求异面直线与所成角的余弦值.
【答案】(1);(2).
【解析】(1)∵在正三棱柱ABC﹣A′B′C′中,底面△ABC边长为2,D为BC的中点,三棱柱体积,
解得高AA′=3,
∴三棱柱的表面积:=
;
(2)取AC中点E,连结DE、C′E,
∵D为BC中点,∴DE∥AB,
∴∠C′DE是异面直线AB与C′D所成角(或所成角的补角),
∵DE=AB=1,C′D=C′E===,
∴cos∠C′DE===.
9.如图,在四棱锥中,平面,,,,,,.
(I)求异面直线与所成角的余弦值;
(II)求证:平面;
(Ⅲ)求直线与平面所成角的正弦值.
【解析】(Ⅰ)如图,由已知AD//BC,故或其补角即为异面直线AP与BC所成的角.
因为AD⊥平面PDC,所以AD⊥PD.
在Rt△PDA中,由已知,得,
故.
所以,异面直线AP与BC所成角的余弦值为.
(Ⅱ)证明:因为AD⊥平面PDC,直线PD平面PDC,所以AD⊥PD.
又因为BC//AD,所以PD⊥BC,
又PD⊥PB,
所以PD⊥平面PBC.
(Ⅲ)过点D作AB的平行线交BC于点F,连结PF,
则DF与平面PBC所成的角等于AB与平面PBC所成的角.
因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,
所以为直线DF和平面PBC所成的角.
由于AD//BC,DF//AB,故BF=AD=1,
由已知,得CF=BC–BF=2.
又AD⊥DC,故BC⊥DC,
在Rt△DCF中,可得,
在Rt△DPF中,可得.
所以,直线AB与平面PBC所成角的正弦值为.
考点:两条异面直线所成的角、直线与平面垂直、直线与平面所成的角
10.如图,在斜三棱柱中,,,,侧面与底面ABC所成的二面角为,E,F分别是棱,的中点.
(Ⅰ)证明:平面;
(Ⅱ)求直线与底面ABC所成的角的大小.
【答案】(Ⅰ)证明见解析;(Ⅱ)
【解析】(Ⅰ)取BC的中点G,连接EG与的交点为P,则点P为EG的中点,连接PF,
在平行四边形中,因为为的中点,所以,
而平面,平面,故平面.
(Ⅱ)过作平面ABC,垂足为H,
连接HC,则就是直线与底面ABC所成的角,
连接AH,并延长交BC于点G,连接GE,
因为,所以为的角平分线,
又因为,所以,G为BC的中点,
因为,,所以,
而,,所以,
于是为二面角的平面角,
由于四边形为平行四边形,得,
因为,所以,
连接,因为,,,所以,
所以,
在直角中,,
故直线与底面ABC所成的角为.
11.如图,在棱长为2的正方体中,已知点M在正方形内部,,.
(1)经过点M在平面内作一条直线与垂直(说明作法及理由);
(2)求直线与平面所成角的余弦值.
【解析】(1)过点M在平面内作一条直线即为所求.
理由如下:连接,在直角中,可计算.
又,,所以点M是的中点,
所以,,,所以平面,
因为平面,所以.
(2)连接与交于点O,易证平面,
所以直线在平面内的射影是,
所以就是直线与平面所成角,在中,.故直线与平面所成角的余弦值为.
12.如图:三棱柱的所有棱长均相等,,为的中点.
(1)求证:平面⊥平面;
(2)求直线与平面所成角的正弦值.
【解析】(1)
如图1,连接CB1交BC1于点O,则O为CB1与BC1的中点,连接EC,EB1
依题意有EB=EC1=EC=EB1
∴EO⊥CB1,EO⊥BC1,
∴EO⊥平面BCC1B1,
∴平面EBC1⊥平面BCC1B1,
(2)如图2取A1B1的中点为H,连接C1H、BH,
∵,∴平面A1B1C1⊥平面BB1A1A,
平面A1B1C1平面BB1A1A=
A1B1,
又∵A1C1=B1C1,H为A1B1的中点,∴C1H⊥A1B1,∴C1H⊥平面BB1A1A,
则∠C1BH为直线BC1与平面BB1A1A所成的角。
令棱长为2a,则C1H=,BC1=,
∴
所以直线BC1与平面BB1A1A所成角的正弦值为
13.如图,在底面为平行四边形的四棱锥中,过点的三条棱PA、AB、AD两两垂直且相等,E,F分别是AC,PB的中点.
(Ⅰ)证明:EF//平面PCD;
(Ⅱ)求EF与平面PAC所成角的大小.
【解析】(Ⅰ)证明:如图,连接BD,则E是BD的中点
又F是PB的中点,∴
EF//PD,
∵
EF不在平面PCD内,∴
EF//平面PCD。
(Ⅱ)连接PE,∵
ABCD是正方形,∴
又平面,∴。
∴平面,故是PD与平面PAC所成的角,
∵EF//PD,∴EF与平面PAC所成的角的大小等于
∵PA=AB=AD,,
∴≌,因此PD=BD
在中,,
∴EF与平面PAC所成角的大小是。
14.如图,在直三棱柱中,是的中点.,,.
(Ⅰ)求直线与平面所成角的正弦值;
(Ⅱ)求二面角的余弦值.
【答案】(Ⅰ);(Ⅱ).
【解析】(Ⅰ)三棱柱是直三棱柱,
平面,,
,是的中点,,
又,平面,
即为直线与平面所成的角,
,,,,
,
直线与平面所成角的正弦值为.
(Ⅱ)作,垂足为,连接,,
,,,,
由可得,
在中,,
在中,即,
即,
即为二面角的平面角,
在中,.
二面角的余弦值为.
15.如图,在平行四边形ABCD中,沿其对角线BD将折起至,使得点在平面ABCD内的射影恰为点B,点E为的中点.
(Ⅰ)求证:平面BDE;
(Ⅱ)若,求与平面BDE所成的角.
【解析】(Ⅰ)如图所示,连接交于点,则为的中点,
连接,因为点为的中点,则,
且平面,平面,所以平面.
(Ⅱ)因为点在平面内的射影恰为点,所以,
从而可知,故,且,
所以平面,则有,
不妨设,则,,,,则,如图所示,在平面与平面上分别过点,作的垂线,垂足重合,记为,
所以平面且平面,故平面平面,
过点作于点,则是与平面所成的角,
在中,,,所以,
又由,所以直线与平面所成的角为.
16.如图在四面体中,平面,,分别为边的中点,为边上任意一点.
(1)证明:平面;
(2)求点到平面的距离.
【解析】(1)由分别为边的中点,所以,
又因为,所以面面,
又因为面,所以面.
(2)因为面,所以,
,面,即,为直角三角形,
,所以,
因为,所以,,
即点到面的距离为.
试卷第1页,总3页
21世纪教育网(www.21cnjy.com)
立体几何大题
1.四棱锥中,侧面为等边三角形且垂直于底面
,
(1)证明:直线平面;
(2)若△面积为,求四棱锥的体积.
【解析】(1)
在平面内,因为,所以
又平面平面故平面
(2)取的中点,连接
由及
得四边形为正方形,则.
因为侧面为等边三角形且垂直于底面,平面平面,
所以底面
因为底面,所以,
设,则,取的中点,连接,则,所以,
因为的面积为,所以,
解得(舍去),
于是
所以四棱锥的体积
2.如图,已知四棱锥,侧面是正三角形,底面为边长2的菱形,,.
(1)设平面平面,求证:;
(2)求多面体的体积;
(3)求二面角的余弦值.
【解析】证明:(1)因为平面平面,
所以平面,
又平面,平面平面,所以;
(2)取中点,连结,由得,
同理,又因为,所以平面,
在中,,所以,
所以多面体的体积
;
(3)由题意知,底面为边长2的菱形,,
所以,又,所以
设的中点为,连结,
由侧面是正三角形知,,所以,
因此就是二面角的平面角,
在中,,,
由余弦定理得,
二面角的余弦值为.
3.如图,正方体,棱长为a,E,F分别为、上的点,且.
(1)当x为何值时,三棱锥的体积最大?
(2)求三棱椎的体积最大时,二面角的正切值;
(3)求异面直线与所成的角的取值范围.
【解析】(1)因为正方体,所以平面
所以,
当时,三棱锥的体积最大.
(2)取中点O,由(1)知,E,F为中点时,三棱锥的体积最大.
所以,因此,,
所以就是二面角的平面角.
在中,
在中,,
三棱椎的体积最大时,二面角的正切值为.
(3)在上取点H使,则在正方形中,
所以,,所以,
所以(或补角)是异面直线与所成的角.
在中,,
在中,,
在中,,
在中,,
因为,所以,所以,
所以,所以
所以异面直线与所成的角的取值范围为.
4.如图所示,四棱锥的底面是边长为2的正方形,底面,为的中点.
(1)求证:平面;
(2)求证:平面;
(3)若三棱锥的体积为,求四棱锥的侧面积.
【解析】(1)连结,交于点.连结,
因为四边形是正方形,所以为的中点,
又为的中点,所以为的中位线,所以,
又平面,平面,所以平面.
(2)因为四边形是正方形,所以,
因为底面,所以,
又,所以平面.
(3)因为,
又因为底面是边长为2的正方形,所以,所以,
又因为是的中点,所以.所以,
所以四棱锥的侧面积
.
5.如图,四棱锥中,底面,,,,,是的中点.
(1)求证:;
(2)求证:面;
(3)求二面角E-AB-C的正切值.
【答案】(1)见解析;(2)见解析;(3)
【解析】(1)证明:∵底面,
又,,故面
面,故
(2)证明:,,故
是的中点,故
由(1)知,从而面,故
易知,故面
(3)过点E作EF⊥AC,垂足为.过点F作FG⊥AB,垂足为G.连结EG
∵PA⊥AC,
∴PA//EF
∴EF⊥底面且F是AC中点
∴故是二面角的一个平面角.
设,则PA=BC=,EF=AF=
从而FG=,故.
6.已知三棱锥中,为等腰直角三角形,,,设点为中点,点为中点,点为上一点,且.
(1)证明:平面;
(2)若,求三棱锥的表面积.
【解析】(1)连接交于点,连接,
点为中点,点为中点,点为的重心,,
,,
又平面,平面,平面.
(2)因为,,,
所以全等于,,,,
所以,
在中,,,则边上的高为,
所以,
.
7.如图,三棱柱中,侧面,已知,,,点是棱的中点.
(1)求证:平面;
(2)求与平面所成角的正弦值.
【解析】(1)由题意,因为,,,由余弦定理可得,
因为,所以,
又因为侧面,所以,
又由,平面,
所以直线平面.
(2)在中,且,可得,
又由且,所以.
又因为,则,即,
因为平面,所以平面,则,
又由平面,平面且,则,
则为所求与平面所成角,
在直角中,所以.
8.如图,在正三棱柱中,底面边长为2,为的中点,三棱柱的体积.
(1)求三棱柱的表面积;
(2)求异面直线与所成角的余弦值.
【答案】(1);(2).
【解析】(1)∵在正三棱柱ABC﹣A′B′C′中,底面△ABC边长为2,D为BC的中点,三棱柱体积,
解得高AA′=3,
∴三棱柱的表面积:=
;
(2)取AC中点E,连结DE、C′E,
∵D为BC中点,∴DE∥AB,
∴∠C′DE是异面直线AB与C′D所成角(或所成角的补角),
∵DE=AB=1,C′D=C′E===,
∴cos∠C′DE===.
9.如图,在四棱锥中,平面,,,,,,.
(I)求异面直线与所成角的余弦值;
(II)求证:平面;
(Ⅲ)求直线与平面所成角的正弦值.
【解析】(Ⅰ)如图,由已知AD//BC,故或其补角即为异面直线AP与BC所成的角.
因为AD⊥平面PDC,所以AD⊥PD.
在Rt△PDA中,由已知,得,
故.
所以,异面直线AP与BC所成角的余弦值为.
(Ⅱ)证明:因为AD⊥平面PDC,直线PD平面PDC,所以AD⊥PD.
又因为BC//AD,所以PD⊥BC,
又PD⊥PB,
所以PD⊥平面PBC.
(Ⅲ)过点D作AB的平行线交BC于点F,连结PF,
则DF与平面PBC所成的角等于AB与平面PBC所成的角.
因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,
所以为直线DF和平面PBC所成的角.
由于AD//BC,DF//AB,故BF=AD=1,
由已知,得CF=BC–BF=2.
又AD⊥DC,故BC⊥DC,
在Rt△DCF中,可得,
在Rt△DPF中,可得.
所以,直线AB与平面PBC所成角的正弦值为.
考点:两条异面直线所成的角、直线与平面垂直、直线与平面所成的角
10.如图,在斜三棱柱中,,,,侧面与底面ABC所成的二面角为,E,F分别是棱,的中点.
(Ⅰ)证明:平面;
(Ⅱ)求直线与底面ABC所成的角的大小.
【答案】(Ⅰ)证明见解析;(Ⅱ)
【解析】(Ⅰ)取BC的中点G,连接EG与的交点为P,则点P为EG的中点,连接PF,
在平行四边形中,因为为的中点,所以,
而平面,平面,故平面.
(Ⅱ)过作平面ABC,垂足为H,
连接HC,则就是直线与底面ABC所成的角,
连接AH,并延长交BC于点G,连接GE,
因为,所以为的角平分线,
又因为,所以,G为BC的中点,
因为,,所以,
而,,所以,
于是为二面角的平面角,
由于四边形为平行四边形,得,
因为,所以,
连接,因为,,,所以,
所以,
在直角中,,
故直线与底面ABC所成的角为.
11.如图,在棱长为2的正方体中,已知点M在正方形内部,,.
(1)经过点M在平面内作一条直线与垂直(说明作法及理由);
(2)求直线与平面所成角的余弦值.
【解析】(1)过点M在平面内作一条直线即为所求.
理由如下:连接,在直角中,可计算.
又,,所以点M是的中点,
所以,,,所以平面,
因为平面,所以.
(2)连接与交于点O,易证平面,
所以直线在平面内的射影是,
所以就是直线与平面所成角,在中,.故直线与平面所成角的余弦值为.
12.如图:三棱柱的所有棱长均相等,,为的中点.
(1)求证:平面⊥平面;
(2)求直线与平面所成角的正弦值.
【解析】(1)
如图1,连接CB1交BC1于点O,则O为CB1与BC1的中点,连接EC,EB1
依题意有EB=EC1=EC=EB1
∴EO⊥CB1,EO⊥BC1,
∴EO⊥平面BCC1B1,
∴平面EBC1⊥平面BCC1B1,
(2)如图2取A1B1的中点为H,连接C1H、BH,
∵,∴平面A1B1C1⊥平面BB1A1A,
平面A1B1C1平面BB1A1A=
A1B1,
又∵A1C1=B1C1,H为A1B1的中点,∴C1H⊥A1B1,∴C1H⊥平面BB1A1A,
则∠C1BH为直线BC1与平面BB1A1A所成的角。
令棱长为2a,则C1H=,BC1=,
∴
所以直线BC1与平面BB1A1A所成角的正弦值为
13.如图,在底面为平行四边形的四棱锥中,过点的三条棱PA、AB、AD两两垂直且相等,E,F分别是AC,PB的中点.
(Ⅰ)证明:EF//平面PCD;
(Ⅱ)求EF与平面PAC所成角的大小.
【解析】(Ⅰ)证明:如图,连接BD,则E是BD的中点
又F是PB的中点,∴
EF//PD,
∵
EF不在平面PCD内,∴
EF//平面PCD。
(Ⅱ)连接PE,∵
ABCD是正方形,∴
又平面,∴。
∴平面,故是PD与平面PAC所成的角,
∵EF//PD,∴EF与平面PAC所成的角的大小等于
∵PA=AB=AD,,
∴≌,因此PD=BD
在中,,
∴EF与平面PAC所成角的大小是。
14.如图,在直三棱柱中,是的中点.,,.
(Ⅰ)求直线与平面所成角的正弦值;
(Ⅱ)求二面角的余弦值.
【答案】(Ⅰ);(Ⅱ).
【解析】(Ⅰ)三棱柱是直三棱柱,
平面,,
,是的中点,,
又,平面,
即为直线与平面所成的角,
,,,,
,
直线与平面所成角的正弦值为.
(Ⅱ)作,垂足为,连接,,
,,,,
由可得,
在中,,
在中,即,
即,
即为二面角的平面角,
在中,.
二面角的余弦值为.
15.如图,在平行四边形ABCD中,沿其对角线BD将折起至,使得点在平面ABCD内的射影恰为点B,点E为的中点.
(Ⅰ)求证:平面BDE;
(Ⅱ)若,求与平面BDE所成的角.
【解析】(Ⅰ)如图所示,连接交于点,则为的中点,
连接,因为点为的中点,则,
且平面,平面,所以平面.
(Ⅱ)因为点在平面内的射影恰为点,所以,
从而可知,故,且,
所以平面,则有,
不妨设,则,,,,则,如图所示,在平面与平面上分别过点,作的垂线,垂足重合,记为,
所以平面且平面,故平面平面,
过点作于点,则是与平面所成的角,
在中,,,所以,
又由,所以直线与平面所成的角为.
16.如图在四面体中,平面,,分别为边的中点,为边上任意一点.
(1)证明:平面;
(2)求点到平面的距离.
【解析】(1)由分别为边的中点,所以,
又因为,所以面面,
又因为面,所以面.
(2)因为面,所以,
,面,即,为直角三角形,
,所以,
因为,所以,,
即点到面的距离为.
试卷第1页,总3页
21世纪教育网(www.21cnjy.com)
