陕西省西安市第六十六中 2019-2020学年高三上学期期末考数学(文)试卷(word含答案
文档属性
| 名称 | 陕西省西安市第六十六中 2019-2020学年高三上学期期末考数学(文)试卷(word含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 462.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-26 11:08:46 | ||
图片预览




文档简介
2019-2020学年高三上学期期末考数学(文)试卷
内容:高中数学全部内容
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设全集,集合,,则(
)
A.
B.
C.
D.
2.若复数z满足,则|z|=(
)
A.5
B.
C.2
D.
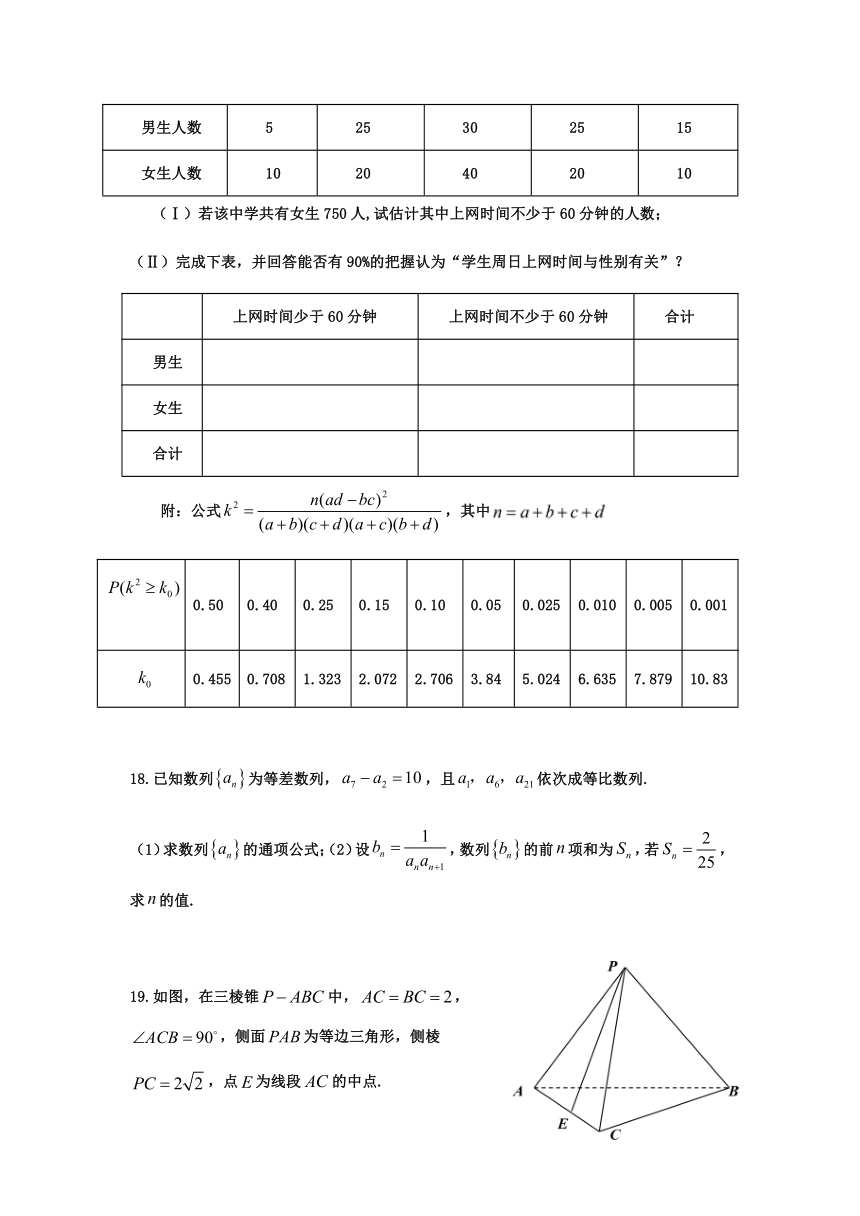
3.如图给出的是计算的值的一个框图,其中菱形判断横应填入的条件是(
)
A.
B.
C.
D.
4.函数的部分图象如图,将的图象向右平移个单位长得到函数的图象,则的单调增区间为(
)
B.
C.
D.
5.如图,正方形中,、分别是、的中点,若,则=(
)
A.2
B.
C.
D.
6.《九章算术》是人类科学史上应用数学的最早巅峰,书中有这样一道题:“今有大夫、不更、簪褭、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何?”其译文是“现有从高到低依次为大夫、不更、簪褭、上造、公士的五个不同爵次的官员,共猎得五只鹿,要按爵次高低分配(即根据爵次高低分配得到的猎物数依次成等差数列),问各得多少鹿?”已知上造分得只鹿,则大夫所得鹿数为(
)
A.
只
B.
只
C.
只
D.
只
7.已知实数满足,则的最大值为(
)
A.-4
B.
C.-1
D.-2
8.一个几何体的三视图如图所示,则该几何体的外接球的表面积为(
)
A.
B.8π
C.
D.
9.现有6个大小相同且分别标有2,3,4,5,6,7的小球,若每次取一个后放回,连续取两次,则所取小球上的数字之积是奇数的概率是(
)
A.
B.
C.
D.
10.已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率的取值范围是
( )
A.
B.
C.(1,2]
D.
11.直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是(
)
A.
B.
C.
D.
12.已知定义在上的函数的导函数为,对任意满足,则下列结论正确的是(
)
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分.
13.设曲线y=a(x-1)-ln
x在点(1,0)处的切线方程为y=2x-2,则a=
14.在中,内角A,B,C所对的边分别为a,b,c,且,
则角=________
15.设P是抛物线y2=4x上的一个动点,若B(4,2),则|PB|+|PF|的最小值为________.
16.给出下列四个命题:
①函数,的图象与直线可能有两个不同的交点;
②函数与函数是相等函数;
③对于指数函数与幂函数,总存在,当时,有成立;
④已知是方程的根,是方程的根,则.
其中正确命题的序号是__________.
三、解答题
17.为了调查某中学学生在周日上网的时间,随机对名男生和名女生进行了不记名的问卷调查,得到了如下的统计结果:
表1:男、女生上网时间与频数分布表
上网时间(分钟)
[30,40)
[40,50)
[50,60)
[60,70)
[70,80]
男生人数
5
25
30
25
15
女生人数
10
20
40
20
10
(Ⅰ)若该中学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(Ⅱ)完成下表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
上网时间少于60分钟
上网时间不少于60分钟
合计
男生
女生
合计
附:公式,其中
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.84
5.024
6.635
7.879
10.83
18.已知数列为等差数列,,且依次成等比数列.
(1)求数列的通项公式;(2)设,数列的前项和为,若,求的值.
19.如图,在三棱锥中,,,侧面为等边三角形,侧棱,点为线段的中点.
(Ⅰ)求证:平面平面;
(Ⅱ)求直线与平面所成角的正弦值.
20已知椭圆E:+=1(a>b>0)经过点P(2,1),且离心率为.
(1)求椭圆的标准方程;(2)设O为坐标原点,在椭圆的短轴上有两点M,N满足=,直线PM,PN分别交椭圆于A,B两点,试证明直线AB过定点.
21.已知函数f(x)=eln
x-ax(a∈R).
(1)讨论f(x)的单调性;
(2)当a=e时,求证:xf(x)-ex+2ex≤0.
请考生在第22、23题中任选一题作答.请用2B铅笔在答题卡上,将所选题号对应的方框涂黑.
22.选修4-4:坐标系与参数方程
在直角坐标系中,,,以为直径的圆记为圆,圆过原点的切线记为,若以原点为极点,轴正半轴为极轴建立极坐标系.
(1)求圆的极坐标方程;
(2)若过点,且与直线垂直的直线与圆交于,两点,求.
23.选修4-5:不等式选讲
已知函数.(Ⅰ)解不等式;
(Ⅱ)求函数的图象与轴围成的三角形面积.
参考答案
1.C
2.B
3.A
4.C
5.B
6.B
7.D
8.B
9.A
10.D
11.A
12.A
13.3
14.B=.
15.5
16.③④
【解析】
【分析】
由函数的定义对①②判断,由指数函数的性质对③判断,利用数形结合思想对④判断.
【详解】
根据函数定义,对定义域内的任意一个值,只有唯一的值与之对应,∴函数,的图象与直线可能有一个或0个交点,因此①错;
中定义域是,函数的定义域是,定义域不相同,不是同一函数,②错;
当时,,因此③正确;
如图,分别是函数、的图象与直线的交点、的横坐标,由于与是互为反函数,它们的图象关于直线对称,而直线与直线垂直,因此两点关于直线对称,直线与直线的交点为,∴.④正确.
故答案为:③④.
17详解:(Ⅰ)设估计上网时间不少于分钟的人数,
依据题意有,解得:,
所以估计其中上网时间不少于分钟的人数是225人.?4分
(Ⅱ)根据题目所给数据得到如下列联表:
上网时间少于60分钟
上网时间不少于60分钟
合计
男生
60
40
100
女生
70
30
100
合计
130
70
200
7分
其中,
因此,没有的把握认为“学生周日上网时间与性别有关”.12分
18解:(1)设数列{an}为公差为d的等差数列,
a7﹣a2=10,即5d=10,即d=2,
a1,a6,a21依次成等比数列,可得
a62=a1a21,即(a1+10)2=a1(a1+40),
解得a1=5,
则an=5+2(n﹣1)=2n+3;.......6分
(2)bn(),
即有前n项和为Sn()
(),
由Sn,可得5n=4n+10,
解得n=10....................12分
19【详解】
解:(Ⅰ)
设中点为,连结,
∵为等边三角形,∴
又,∴
由已知,,
∴,
又为正三角形,且,∴.
∵,∴.
∴
即
∴面
∴平面平面.
....................
6分
(Ⅱ)设中点为,连结
∵点为线段的中点,∴∥
由(Ⅰ)知平面.
∴
平面
∴是直线与平面所成的角.
由(Ⅰ)与已知得,∴,
又,∴
又,
在中,
∴直线与平面所成角的正弦值为...................12分
20解:由椭圆的离心率e===,得a2=4b2,将P(2,1)代入椭圆方程+=1,得+=1,解得b2=2,则a2=8,所以椭圆的标准方程为+=1.........5分
(2)证明:当M,N分别是短轴的端点时,显然直线AB为y轴,所以若直线AB过定点,则这个定点一定在y轴上,
当M,N不是短轴的端点时,设直线AB的方程为y=kx+t,设A(x1,y1),B(x2,y2),易知x1≠2,x2≠2,
联立消去y,得(1+4k2)x2+8ktx+4t2-8=0,则Δ=16(8k2-t2+2)>0,
x1+x2=-,x1x2=.
又直线PA的方程为y-1=(x-2),
即y-1=(x-2),
所以点M的坐标为,
同理可知N,
由=,得+=0,
化简整理得,(2-4k)x1x2-(2-4k+2t)(x1+x2)+8t=0,
则(2-4k)×-(2-4k+2t)+8t=0,
整理得(2t+4)k+(t2+t-2)=0,
当且仅当t=-2时,上式对任意的k都成立,
所以直线AB过定点(0,-2).............................12分
21解:f′(x)=-a(x>0),
①若a≤0,则f′(x)>0,f(x)在(0,+∞)上单调递增;
②若a>0,令f′(x)=0,得x=,
则当00;当x>时,f′(x)<0,
故f(x)在上单调递增,在上单调...................5分
解:证明:因为x>0,所以只需证f(x)≤-2e,
当a=e时,由(1)知,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)max=f(1)=-e.
记g(x)=-2e(x>0),则g′(x)=,
当01时,g′(x)>0,g(x)单调递增,
所以g(x)min=g(1)=-e.
综上,当x>0时,f(x)≤g(x),即f(x)≤-2e,即xf(x)-ex+2ex≤0......12分
22.(1)(2)1
试题解析:(1)由题意,知圆的直径,圆心的坐标为,
∴圆的直角坐标为,即,
将,代入上式,
得到圆的极坐标方程为. ..................5分
(2)∵直线与圆过原点的切线垂直
∴直线的倾斜角为,斜率为,
又∵直线过点
∴直线的普通方程为,即,
∴圆心到直线的距离,
∴...........10分
23试题解析:解:(Ⅰ)由题意可得,
因为,
所以当时,由,解得,即;
当时,由,解得,即;
当时,,解得,即;
故不等式的解集为.....................5分
(Ⅱ)如图画出函数的图象,
可得函数的图象与轴交点的横坐标分别为,
即函数的图象与轴围成的三角形面积为...............12分
答案第1页,总2页
内容:高中数学全部内容
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设全集,集合,,则(
)
A.
B.
C.
D.
2.若复数z满足,则|z|=(
)
A.5
B.
C.2
D.
3.如图给出的是计算的值的一个框图,其中菱形判断横应填入的条件是(
)
A.
B.
C.
D.
4.函数的部分图象如图,将的图象向右平移个单位长得到函数的图象,则的单调增区间为(
)
B.
C.
D.
5.如图,正方形中,、分别是、的中点,若,则=(
)
A.2
B.
C.
D.
6.《九章算术》是人类科学史上应用数学的最早巅峰,书中有这样一道题:“今有大夫、不更、簪褭、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何?”其译文是“现有从高到低依次为大夫、不更、簪褭、上造、公士的五个不同爵次的官员,共猎得五只鹿,要按爵次高低分配(即根据爵次高低分配得到的猎物数依次成等差数列),问各得多少鹿?”已知上造分得只鹿,则大夫所得鹿数为(
)
A.
只
B.
只
C.
只
D.
只
7.已知实数满足,则的最大值为(
)
A.-4
B.
C.-1
D.-2
8.一个几何体的三视图如图所示,则该几何体的外接球的表面积为(
)
A.
B.8π
C.
D.
9.现有6个大小相同且分别标有2,3,4,5,6,7的小球,若每次取一个后放回,连续取两次,则所取小球上的数字之积是奇数的概率是(
)
A.
B.
C.
D.
10.已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率的取值范围是
( )
A.
B.
C.(1,2]
D.
11.直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是(
)
A.
B.
C.
D.
12.已知定义在上的函数的导函数为,对任意满足,则下列结论正确的是(
)
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分.
13.设曲线y=a(x-1)-ln
x在点(1,0)处的切线方程为y=2x-2,则a=
14.在中,内角A,B,C所对的边分别为a,b,c,且,
则角=________
15.设P是抛物线y2=4x上的一个动点,若B(4,2),则|PB|+|PF|的最小值为________.
16.给出下列四个命题:
①函数,的图象与直线可能有两个不同的交点;
②函数与函数是相等函数;
③对于指数函数与幂函数,总存在,当时,有成立;
④已知是方程的根,是方程的根,则.
其中正确命题的序号是__________.
三、解答题
17.为了调查某中学学生在周日上网的时间,随机对名男生和名女生进行了不记名的问卷调查,得到了如下的统计结果:
表1:男、女生上网时间与频数分布表
上网时间(分钟)
[30,40)
[40,50)
[50,60)
[60,70)
[70,80]
男生人数
5
25
30
25
15
女生人数
10
20
40
20
10
(Ⅰ)若该中学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(Ⅱ)完成下表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
上网时间少于60分钟
上网时间不少于60分钟
合计
男生
女生
合计
附:公式,其中
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.84
5.024
6.635
7.879
10.83
18.已知数列为等差数列,,且依次成等比数列.
(1)求数列的通项公式;(2)设,数列的前项和为,若,求的值.
19.如图,在三棱锥中,,,侧面为等边三角形,侧棱,点为线段的中点.
(Ⅰ)求证:平面平面;
(Ⅱ)求直线与平面所成角的正弦值.
20已知椭圆E:+=1(a>b>0)经过点P(2,1),且离心率为.
(1)求椭圆的标准方程;(2)设O为坐标原点,在椭圆的短轴上有两点M,N满足=,直线PM,PN分别交椭圆于A,B两点,试证明直线AB过定点.
21.已知函数f(x)=eln
x-ax(a∈R).
(1)讨论f(x)的单调性;
(2)当a=e时,求证:xf(x)-ex+2ex≤0.
请考生在第22、23题中任选一题作答.请用2B铅笔在答题卡上,将所选题号对应的方框涂黑.
22.选修4-4:坐标系与参数方程
在直角坐标系中,,,以为直径的圆记为圆,圆过原点的切线记为,若以原点为极点,轴正半轴为极轴建立极坐标系.
(1)求圆的极坐标方程;
(2)若过点,且与直线垂直的直线与圆交于,两点,求.
23.选修4-5:不等式选讲
已知函数.(Ⅰ)解不等式;
(Ⅱ)求函数的图象与轴围成的三角形面积.
参考答案
1.C
2.B
3.A
4.C
5.B
6.B
7.D
8.B
9.A
10.D
11.A
12.A
13.3
14.B=.
15.5
16.③④
【解析】
【分析】
由函数的定义对①②判断,由指数函数的性质对③判断,利用数形结合思想对④判断.
【详解】
根据函数定义,对定义域内的任意一个值,只有唯一的值与之对应,∴函数,的图象与直线可能有一个或0个交点,因此①错;
中定义域是,函数的定义域是,定义域不相同,不是同一函数,②错;
当时,,因此③正确;
如图,分别是函数、的图象与直线的交点、的横坐标,由于与是互为反函数,它们的图象关于直线对称,而直线与直线垂直,因此两点关于直线对称,直线与直线的交点为,∴.④正确.
故答案为:③④.
17详解:(Ⅰ)设估计上网时间不少于分钟的人数,
依据题意有,解得:,
所以估计其中上网时间不少于分钟的人数是225人.?4分
(Ⅱ)根据题目所给数据得到如下列联表:
上网时间少于60分钟
上网时间不少于60分钟
合计
男生
60
40
100
女生
70
30
100
合计
130
70
200
7分
其中,
因此,没有的把握认为“学生周日上网时间与性别有关”.12分
18解:(1)设数列{an}为公差为d的等差数列,
a7﹣a2=10,即5d=10,即d=2,
a1,a6,a21依次成等比数列,可得
a62=a1a21,即(a1+10)2=a1(a1+40),
解得a1=5,
则an=5+2(n﹣1)=2n+3;.......6分
(2)bn(),
即有前n项和为Sn()
(),
由Sn,可得5n=4n+10,
解得n=10....................12分
19【详解】
解:(Ⅰ)
设中点为,连结,
∵为等边三角形,∴
又,∴
由已知,,
∴,
又为正三角形,且,∴.
∵,∴.
∴
即
∴面
∴平面平面.
....................
6分
(Ⅱ)设中点为,连结
∵点为线段的中点,∴∥
由(Ⅰ)知平面.
∴
平面
∴是直线与平面所成的角.
由(Ⅰ)与已知得,∴,
又,∴
又,
在中,
∴直线与平面所成角的正弦值为...................12分
20解:由椭圆的离心率e===,得a2=4b2,将P(2,1)代入椭圆方程+=1,得+=1,解得b2=2,则a2=8,所以椭圆的标准方程为+=1.........5分
(2)证明:当M,N分别是短轴的端点时,显然直线AB为y轴,所以若直线AB过定点,则这个定点一定在y轴上,
当M,N不是短轴的端点时,设直线AB的方程为y=kx+t,设A(x1,y1),B(x2,y2),易知x1≠2,x2≠2,
联立消去y,得(1+4k2)x2+8ktx+4t2-8=0,则Δ=16(8k2-t2+2)>0,
x1+x2=-,x1x2=.
又直线PA的方程为y-1=(x-2),
即y-1=(x-2),
所以点M的坐标为,
同理可知N,
由=,得+=0,
化简整理得,(2-4k)x1x2-(2-4k+2t)(x1+x2)+8t=0,
则(2-4k)×-(2-4k+2t)+8t=0,
整理得(2t+4)k+(t2+t-2)=0,
当且仅当t=-2时,上式对任意的k都成立,
所以直线AB过定点(0,-2).............................12分
21解:f′(x)=-a(x>0),
①若a≤0,则f′(x)>0,f(x)在(0,+∞)上单调递增;
②若a>0,令f′(x)=0,得x=,
则当0
故f(x)在上单调递增,在上单调...................5分
解:证明:因为x>0,所以只需证f(x)≤-2e,
当a=e时,由(1)知,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)max=f(1)=-e.
记g(x)=-2e(x>0),则g′(x)=,
当0
所以g(x)min=g(1)=-e.
综上,当x>0时,f(x)≤g(x),即f(x)≤-2e,即xf(x)-ex+2ex≤0......12分
22.(1)(2)1
试题解析:(1)由题意,知圆的直径,圆心的坐标为,
∴圆的直角坐标为,即,
将,代入上式,
得到圆的极坐标方程为. ..................5分
(2)∵直线与圆过原点的切线垂直
∴直线的倾斜角为,斜率为,
又∵直线过点
∴直线的普通方程为,即,
∴圆心到直线的距离,
∴...........10分
23试题解析:解:(Ⅰ)由题意可得,
因为,
所以当时,由,解得,即;
当时,由,解得,即;
当时,,解得,即;
故不等式的解集为.....................5分
(Ⅱ)如图画出函数的图象,
可得函数的图象与轴交点的横坐标分别为,
即函数的图象与轴围成的三角形面积为...............12分
答案第1页,总2页
同课章节目录
