第23章 旋转复习课(旋转模型一)(共22张PPT)
文档属性
| 名称 | 第23章 旋转复习课(旋转模型一)(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-26 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
人教版
九上
第23章旋转
复习
模型一:等线段共点
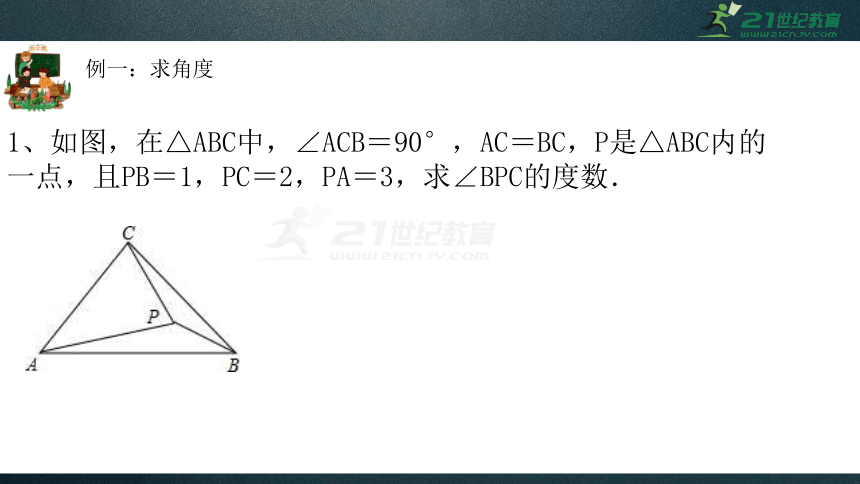
例一:求角度
1、如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且PB=1,PC=2,PA=3,求∠BPC的度数.
【解答】解:如图,把△ACP绕点C逆时针旋转90°得到△BCD,连
接DP,∵△ACP绕点C逆时针旋转90°得到△BCD,
∴CP=CD=2,∠DCP=90°,DB=PA=3,
∴△CPD为等腰直角三角形,
∴PD=PC=2,∠CPD=45°,
在△PDB中,PB=1,PD=2,DB=3,
而
∴PB2+PD2=BD2,
∴△PBD为直角三角形,
∴∠DPB=90°,
∴∠BPC=45°+90°=135°
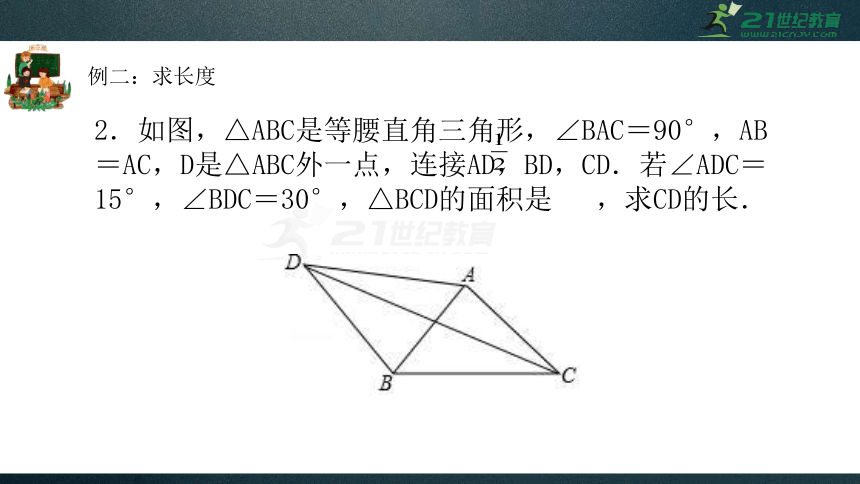
例二:求长度
2.如图,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,D是△ABC外一点,连接AD,BD,CD.若∠ADC=15°,∠BDC=30°,△BCD的面积是
,求CD的长.
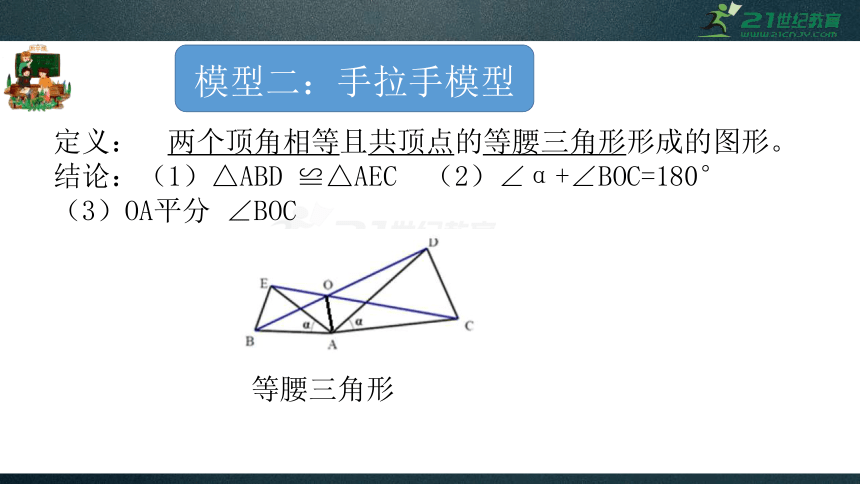
模型二:手拉手模型
定义:
两个顶角相等且共顶点的等腰三角形形成的图形。
结论:(1)△ABD
≌△AEC
(2)∠α+∠BOC=180°
(3)OA平分
∠BOC
等腰三角形
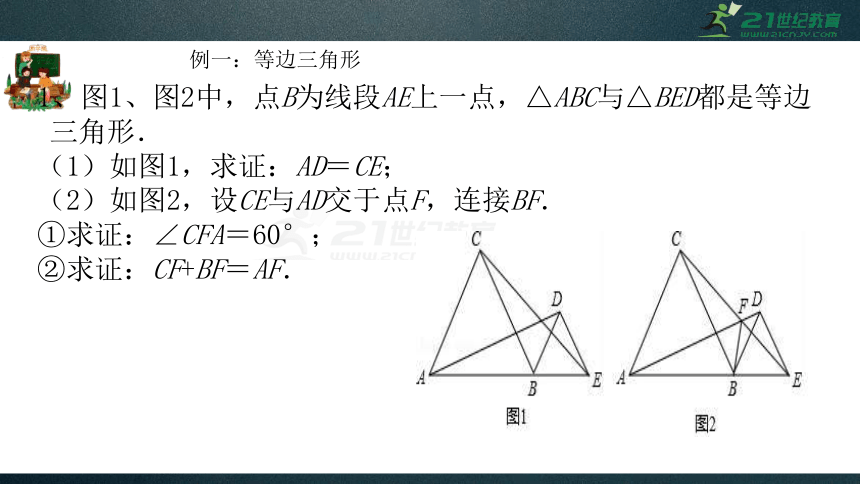
例一:等边三角形
1、图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形.
(1)如图1,求证:AD=CE;
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=60°;
②求证:CF+BF=AF.
2.如图,两个正方形ABCD和DEFG,连接AG与CE,二者相交于H
问:(1)△ADG≌△CDE是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分∠AHE?
(5)线段AC、GE、AE、CG有什么数量关系?
例二:正方形
课后练习
1、(1)在一次数学探究活动中,陈老师给出了一道题.
如图1,已知△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且PA=3,PB=1,PC=2,求∠BPC的度数.
小强在解决此题时,是将△APC绕C旋转到△CBE的位置(即过C作CE⊥CP,且使CE=CP,连接EP、EB).你知道小强是怎么解决的吗?
(2)请根据(1)的思想解决以下问题:
如图2所示,设P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
【解答】解:(1)如图1,由题意得:∠PCE=90°
PC=EC=2;BE=PA=3;
由勾股定理得:PE2=22+22=8;
∵PB2=1,BE2=9,
∴BE2=PE2+PB2,
∴∠BPE=90°,
∵∠CPE=45°,
∴∠BPC=135°.
(2)如图2,将△ABP绕点A逆时针旋转60°到△ACQ的位置,连接PQ;
则AP=AQ,∠PAQ=60°,QC=PB=4;
∴△APQ为等边三角形,∠AQP=60°,PQ=PA=3;
∵PQ2+CQ2=32+42=25,PC2=52=25,
∴PQ2+CQ2=PC2,
∴∠PQC=90°,∠AQC=60°+90°=150°,
∴∠APB=∠AQC=150°
2.已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD⊥CF.BD=CF.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,第(1)问结论还成立吗?并说明理由.
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:
①请直接写出CF、BC、CD三条线段之间的关系.
②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
【解答】(1)证明:∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
∴△BAD≌△CAF(SAS),
∴BD=CF,∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴BD⊥CF;
(2)(1)的结论仍然成立,理由:
∵∠BAD=∠BAC+∠CAD=90°+∠CAD,
∠CAF=∠DAF+∠CAD=90°+∠CAD,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
∴△BAD≌△CAF(SAS),
∴BD=CF,∠ACF=∠ABD=45°
∴∠BCF=∠ACB+∠ACF=45°+45°=90°
∴BD⊥CF.
(3)①BC、CD与CF的关系:CD=BC+CF
理由:与(1)同法可证△BAD≌△CAF,从而可得:
BD=CF,
即:CD=BC+CF
②△AOC是等腰三角形
理由:与(1)同法可证△BAD≌△CAF,可得:∠DBA=∠FCA,
又∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
则∠ABD=180°﹣45°=135°,
∴∠ABD=∠FCA=135°
∴∠DCF=135°﹣45°=90°
∴△FCD为直角三角形.
又∵四边形ADEF是正方形,对角线AE与DF相交于点O,
∴OC=
DF,
∴OC=OA
∴△AOC是等腰三角形.
https://www.21cnjy.com/help/help_extract.php
人教版
九上
第23章旋转
复习
模型一:等线段共点
例一:求角度
1、如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且PB=1,PC=2,PA=3,求∠BPC的度数.
【解答】解:如图,把△ACP绕点C逆时针旋转90°得到△BCD,连
接DP,∵△ACP绕点C逆时针旋转90°得到△BCD,
∴CP=CD=2,∠DCP=90°,DB=PA=3,
∴△CPD为等腰直角三角形,
∴PD=PC=2,∠CPD=45°,
在△PDB中,PB=1,PD=2,DB=3,
而
∴PB2+PD2=BD2,
∴△PBD为直角三角形,
∴∠DPB=90°,
∴∠BPC=45°+90°=135°
例二:求长度
2.如图,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,D是△ABC外一点,连接AD,BD,CD.若∠ADC=15°,∠BDC=30°,△BCD的面积是
,求CD的长.
模型二:手拉手模型
定义:
两个顶角相等且共顶点的等腰三角形形成的图形。
结论:(1)△ABD
≌△AEC
(2)∠α+∠BOC=180°
(3)OA平分
∠BOC
等腰三角形
例一:等边三角形
1、图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形.
(1)如图1,求证:AD=CE;
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=60°;
②求证:CF+BF=AF.
2.如图,两个正方形ABCD和DEFG,连接AG与CE,二者相交于H
问:(1)△ADG≌△CDE是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分∠AHE?
(5)线段AC、GE、AE、CG有什么数量关系?
例二:正方形
课后练习
1、(1)在一次数学探究活动中,陈老师给出了一道题.
如图1,已知△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且PA=3,PB=1,PC=2,求∠BPC的度数.
小强在解决此题时,是将△APC绕C旋转到△CBE的位置(即过C作CE⊥CP,且使CE=CP,连接EP、EB).你知道小强是怎么解决的吗?
(2)请根据(1)的思想解决以下问题:
如图2所示,设P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
【解答】解:(1)如图1,由题意得:∠PCE=90°
PC=EC=2;BE=PA=3;
由勾股定理得:PE2=22+22=8;
∵PB2=1,BE2=9,
∴BE2=PE2+PB2,
∴∠BPE=90°,
∵∠CPE=45°,
∴∠BPC=135°.
(2)如图2,将△ABP绕点A逆时针旋转60°到△ACQ的位置,连接PQ;
则AP=AQ,∠PAQ=60°,QC=PB=4;
∴△APQ为等边三角形,∠AQP=60°,PQ=PA=3;
∵PQ2+CQ2=32+42=25,PC2=52=25,
∴PQ2+CQ2=PC2,
∴∠PQC=90°,∠AQC=60°+90°=150°,
∴∠APB=∠AQC=150°
2.已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD⊥CF.BD=CF.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,第(1)问结论还成立吗?并说明理由.
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:
①请直接写出CF、BC、CD三条线段之间的关系.
②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
【解答】(1)证明:∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
∴△BAD≌△CAF(SAS),
∴BD=CF,∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴BD⊥CF;
(2)(1)的结论仍然成立,理由:
∵∠BAD=∠BAC+∠CAD=90°+∠CAD,
∠CAF=∠DAF+∠CAD=90°+∠CAD,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
∴△BAD≌△CAF(SAS),
∴BD=CF,∠ACF=∠ABD=45°
∴∠BCF=∠ACB+∠ACF=45°+45°=90°
∴BD⊥CF.
(3)①BC、CD与CF的关系:CD=BC+CF
理由:与(1)同法可证△BAD≌△CAF,从而可得:
BD=CF,
即:CD=BC+CF
②△AOC是等腰三角形
理由:与(1)同法可证△BAD≌△CAF,可得:∠DBA=∠FCA,
又∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
则∠ABD=180°﹣45°=135°,
∴∠ABD=∠FCA=135°
∴∠DCF=135°﹣45°=90°
∴△FCD为直角三角形.
又∵四边形ADEF是正方形,对角线AE与DF相交于点O,
∴OC=
DF,
∴OC=OA
∴△AOC是等腰三角形.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
