一元二次方程根与系数关系
文档属性
| 名称 | 一元二次方程根与系数关系 |

|
|
| 格式 | rar | ||
| 文件大小 | 304.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-08 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
22.2.4
一元二次方程的
根与系数的关系
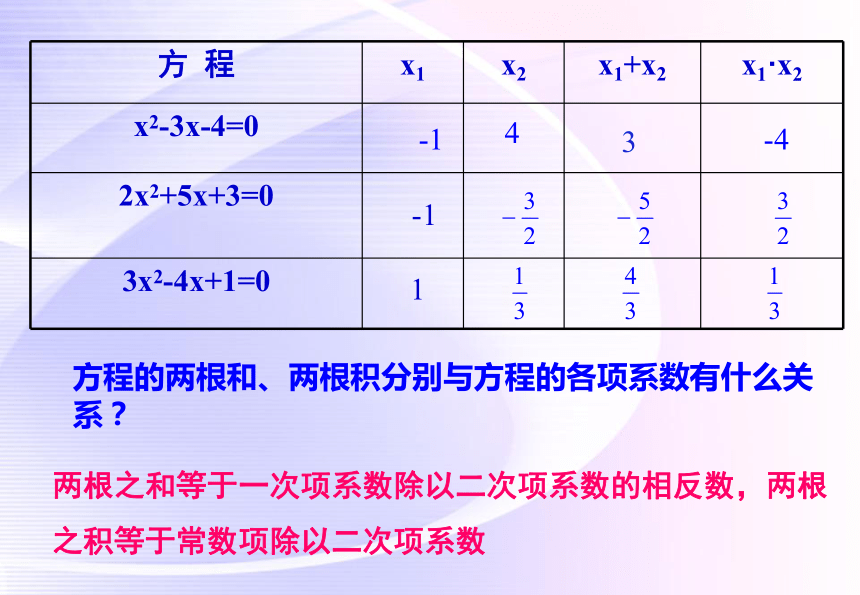
方 程 x1 x2 x1+x2 x1·x2
x2-3x-4=0
2x2+5x+3=0
3x2-4x+1=0
方程的两根和、两根积分别与方程的各项系数有什么关系?
两根之和等于一次项系数除以二次项系数的相反数,两根之积等于常数项除以二次项系数
4
-1
1
-4
-1
3
一元二次方程 ,当 时,
由求根公式可知方程的两根为
因此,方程的两根 ,和系数
有如下的关系:
一元二次方程根与系数的关系
(韦达定理)
推论1
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用X1+X2=- 时,
注意“- ”不要漏写。
说出下列各方程的两根之和与两根之积:
1、x2 - 2x - 1=0
2、2x2 - 3x + =0
3、2x2 - 6x =0
4、3x2+x+2 = 4
x1+x2=2
x1x2=-1
x1+x2=3
x1x2=0
x1+x2=
x1x2=
x1+x2=
对于方程x2+2x+3=0,小明说它的两根之和为-2,
两根之积为3,你认为他的说法对吗?为什么?
x1x2=
1、课本P41例4
2、利用根与系数的关系,求作一个一元二次方程,使它的两根为2和3.
3、如果 是方程2X2+mX+3=0的一个根,求它的另一个根及m的值.
1、如果-1是方程2X2-X+m=0的一个根,则另
一个根是___,m =____。
2、设 X1、X2是方程X2-4X+1=0的两个根,则
X1+X2 = ___ ,X1X2 = ____,
X12+X22 = ( X1+X2)2 - ___ = ___
( X1-X2)2 = ( ___ )2 - 4X1X2 = ___
3、判断正误:
以2和-3为根的方程是X2-X-6=0 ( )
4、已知两个数的和是1,积是-2,则这两个数是
_____ 。
X1+X2
2X1X2
-3
4
1
14
12
×
2和-1
基础练习
(还有其他解法吗?)
5、以方程X2+3X+2=0的两个根的相反数为根的方
程是( )
A、y2+3y-2=0 B、 y2-3y+2=0
C、y2+3y+2=0 D、 y2-3y-2=0
此题还有其他解法吗?
B
换元法:
基础练习
设y=-x,则x=-y,将其代入X2+3X+2=0,
得y2-3y+2=0 ,即为所求方程。
6. 已知2x2+3x-6=0的两根是x1 ,x2 ,
不解方程求下列各式的值。
(1)
(2)
练习1
已知关于x的方程
当m= 时,此方程的两根互为相反数.
当m= 时,此方程的两根互为倒数.
-1
1
分析:1.
2.
4
1
14
12
题3
则:
=
=
应用:一求值
另外几种常见的求值
求与方程的根有关的代数式的值时,
一般先将所求的代数式化成含两根之和,
两根之积的形式,再整体代入.
练习2
设 的两个实数根
为 则: 的值为( )
A. 1 B. -1 C. D.
A
以 为两根的一元二次方程
(二次项系数为1)为:
二 已知两根求作新的方程
题4.
点p(m,n)既在反比例函数 的
图象上, 又在一次函数 的图象上,
则以m,n为根的一元二次方程为(二次项系数为1):
解:由已知得,
{
即
m·n=-2
m+n=-2
{
∴所求一元二次方程为:
题5 以方程X2+3X-5=0的两个根的相反数为根的方程是( )
A、y2+3y-5=0 B、 y2-3y-5=0
C、y2+3y+5=0 D、 y2-3y+5=0
B
分析:设原方程两根为 则:
新方程的两根之和为
新方程的两根之积为
求作新的一元二次方程时:
1.先求原方程的两根和与两根积.
2.利用新方程的两根与原方程的两根之
间的关系,求新方程的两根和与两根积.
(或由已知求新方程的两根和与两根积)
3.利用新方程的两根和与两根积,
求作新的一元二次方程.
练习:
1.以2和 -3为根的一元二次方程
(二次项系数为1)为:
题6 已知两个数的和是1,积是-2,则两 个数是 。
2和-1
解法(一):设两数分别为x,y则:
{
解得:
x=2
y=-1
{
或
x=-1
y=2
{
解法(二):设两数分别为一个一元二次方程
的两根则:
求得
∴两数为2,-1
三 已知两个数的和与积,求两数
题7 如果-1是方程
的一个根,则另一个根是___m=____。
(还有其他解法吗?)
-3
四 求方程中的待定系数
题8 已知方程 的两个实数根
是 且 求k的值。
解:由根与系数的关系得
X1+X2=-k, X1×X2=k+2
又 X12+ X2 2 = 4
即(X1+ X2)2 -2X1X2=4
K2- 2(k+2)=4
K2-2k-8=0
∵ △= K2-4k-8
当k=4时, △<0
当k=-2时,△>0
∴ k=-2
解得:k=4 或k=-2
题9 在△ABC中a,b,c分别为∠A, ∠B,∠C
的对边,且c= ,若关于x的方程
有两个相等的实数根,又方程
的两实数根的平方和为6,求△ABC的面积.
五 综合
小结:
1、熟练掌握根与系数的关系;
2、灵活运用根与系数关系解决问题;
3、探索解题思路,归纳解题思想方法。
作业:试卷《课后练习》
题9 方程
有一个正根,一个负根,求m的取值范围。
解:由已知,
△=
{
即
{
m>0
m-1<0
∴0一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0
X1+X2>0
两个负根
△≥0
X1X2>0
X1+X2<0
{
{
{
22.2.4
一元二次方程的
根与系数的关系
方 程 x1 x2 x1+x2 x1·x2
x2-3x-4=0
2x2+5x+3=0
3x2-4x+1=0
方程的两根和、两根积分别与方程的各项系数有什么关系?
两根之和等于一次项系数除以二次项系数的相反数,两根之积等于常数项除以二次项系数
4
-1
1
-4
-1
3
一元二次方程 ,当 时,
由求根公式可知方程的两根为
因此,方程的两根 ,和系数
有如下的关系:
一元二次方程根与系数的关系
(韦达定理)
推论1
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用X1+X2=- 时,
注意“- ”不要漏写。
说出下列各方程的两根之和与两根之积:
1、x2 - 2x - 1=0
2、2x2 - 3x + =0
3、2x2 - 6x =0
4、3x2+x+2 = 4
x1+x2=2
x1x2=-1
x1+x2=3
x1x2=0
x1+x2=
x1x2=
x1+x2=
对于方程x2+2x+3=0,小明说它的两根之和为-2,
两根之积为3,你认为他的说法对吗?为什么?
x1x2=
1、课本P41例4
2、利用根与系数的关系,求作一个一元二次方程,使它的两根为2和3.
3、如果 是方程2X2+mX+3=0的一个根,求它的另一个根及m的值.
1、如果-1是方程2X2-X+m=0的一个根,则另
一个根是___,m =____。
2、设 X1、X2是方程X2-4X+1=0的两个根,则
X1+X2 = ___ ,X1X2 = ____,
X12+X22 = ( X1+X2)2 - ___ = ___
( X1-X2)2 = ( ___ )2 - 4X1X2 = ___
3、判断正误:
以2和-3为根的方程是X2-X-6=0 ( )
4、已知两个数的和是1,积是-2,则这两个数是
_____ 。
X1+X2
2X1X2
-3
4
1
14
12
×
2和-1
基础练习
(还有其他解法吗?)
5、以方程X2+3X+2=0的两个根的相反数为根的方
程是( )
A、y2+3y-2=0 B、 y2-3y+2=0
C、y2+3y+2=0 D、 y2-3y-2=0
此题还有其他解法吗?
B
换元法:
基础练习
设y=-x,则x=-y,将其代入X2+3X+2=0,
得y2-3y+2=0 ,即为所求方程。
6. 已知2x2+3x-6=0的两根是x1 ,x2 ,
不解方程求下列各式的值。
(1)
(2)
练习1
已知关于x的方程
当m= 时,此方程的两根互为相反数.
当m= 时,此方程的两根互为倒数.
-1
1
分析:1.
2.
4
1
14
12
题3
则:
=
=
应用:一求值
另外几种常见的求值
求与方程的根有关的代数式的值时,
一般先将所求的代数式化成含两根之和,
两根之积的形式,再整体代入.
练习2
设 的两个实数根
为 则: 的值为( )
A. 1 B. -1 C. D.
A
以 为两根的一元二次方程
(二次项系数为1)为:
二 已知两根求作新的方程
题4.
点p(m,n)既在反比例函数 的
图象上, 又在一次函数 的图象上,
则以m,n为根的一元二次方程为(二次项系数为1):
解:由已知得,
{
即
m·n=-2
m+n=-2
{
∴所求一元二次方程为:
题5 以方程X2+3X-5=0的两个根的相反数为根的方程是( )
A、y2+3y-5=0 B、 y2-3y-5=0
C、y2+3y+5=0 D、 y2-3y+5=0
B
分析:设原方程两根为 则:
新方程的两根之和为
新方程的两根之积为
求作新的一元二次方程时:
1.先求原方程的两根和与两根积.
2.利用新方程的两根与原方程的两根之
间的关系,求新方程的两根和与两根积.
(或由已知求新方程的两根和与两根积)
3.利用新方程的两根和与两根积,
求作新的一元二次方程.
练习:
1.以2和 -3为根的一元二次方程
(二次项系数为1)为:
题6 已知两个数的和是1,积是-2,则两 个数是 。
2和-1
解法(一):设两数分别为x,y则:
{
解得:
x=2
y=-1
{
或
x=-1
y=2
{
解法(二):设两数分别为一个一元二次方程
的两根则:
求得
∴两数为2,-1
三 已知两个数的和与积,求两数
题7 如果-1是方程
的一个根,则另一个根是___m=____。
(还有其他解法吗?)
-3
四 求方程中的待定系数
题8 已知方程 的两个实数根
是 且 求k的值。
解:由根与系数的关系得
X1+X2=-k, X1×X2=k+2
又 X12+ X2 2 = 4
即(X1+ X2)2 -2X1X2=4
K2- 2(k+2)=4
K2-2k-8=0
∵ △= K2-4k-8
当k=4时, △<0
当k=-2时,△>0
∴ k=-2
解得:k=4 或k=-2
题9 在△ABC中a,b,c分别为∠A, ∠B,∠C
的对边,且c= ,若关于x的方程
有两个相等的实数根,又方程
的两实数根的平方和为6,求△ABC的面积.
五 综合
小结:
1、熟练掌握根与系数的关系;
2、灵活运用根与系数关系解决问题;
3、探索解题思路,归纳解题思想方法。
作业:试卷《课后练习》
题9 方程
有一个正根,一个负根,求m的取值范围。
解:由已知,
△=
{
即
{
m>0
m-1<0
∴0
△>0
X1X2<0
两个正根
△≥0
X1X2>0
X1+X2>0
两个负根
△≥0
X1X2>0
X1+X2<0
{
{
{
同课章节目录
