直线的倾斜角和斜率
图片预览






文档简介
(共25张PPT)
o
直线的倾斜角和斜率
在直角坐标系中如何确定直线的位置呢?
.
Q
.
P
O
x
y
问题探究
方法一:两点确定一条直线
P
y
o
x
.
问题1:过定点P的直线有几条?
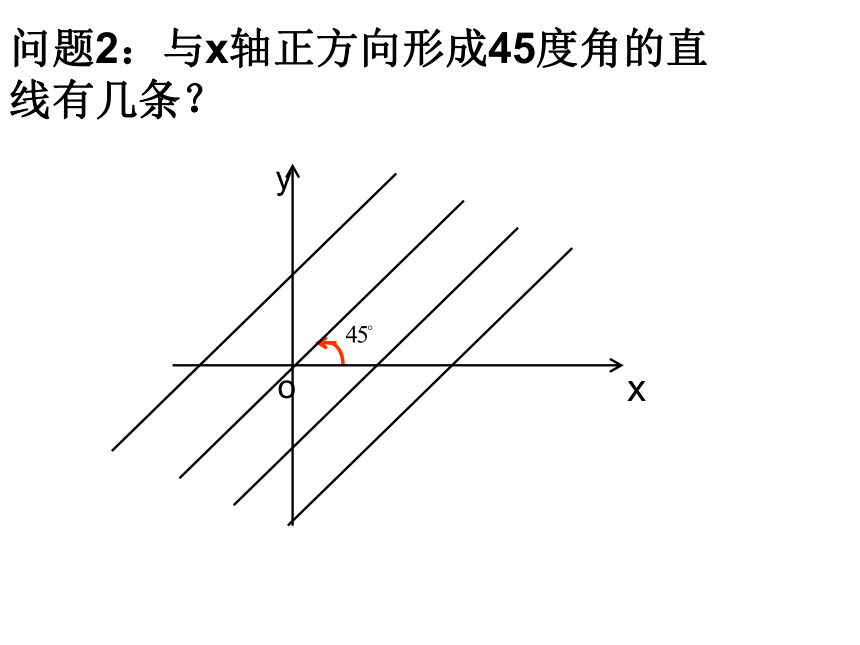
问题2:与x轴正方向形成45度角的直线有几条?
y
o
x
P
y
o
x
.
问题3:过点P,与x轴正方向形成45度角的直线有几条?
而直线的方向我们就是用倾斜角来刻画的。
总 结 归 纳
在平面直角坐标系中,确定一条直线位置确定的几何条件是:已知直线上的一个点和这条直线的方向。
P
y
o
x
.
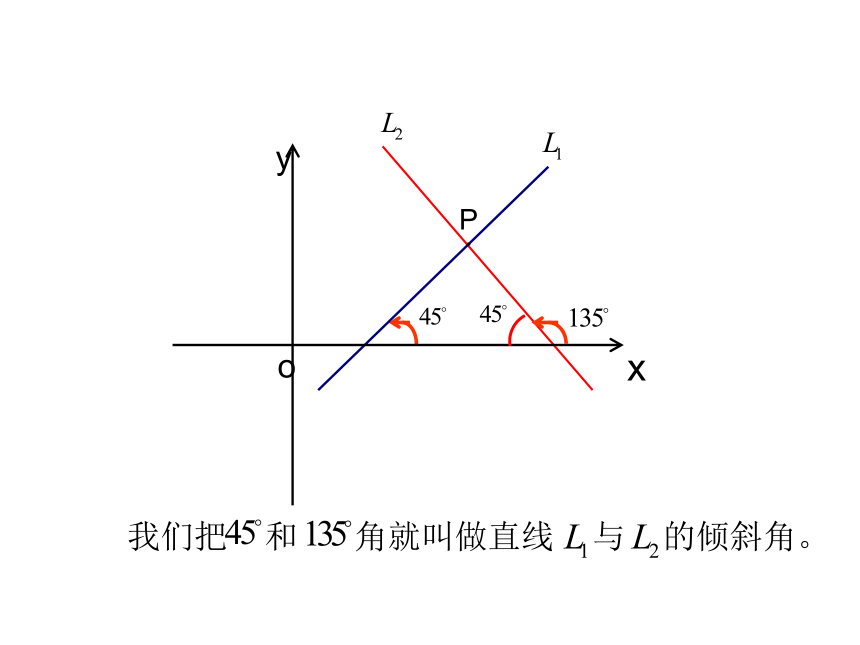
我们把 和 角就叫做直线 与 的倾斜角。
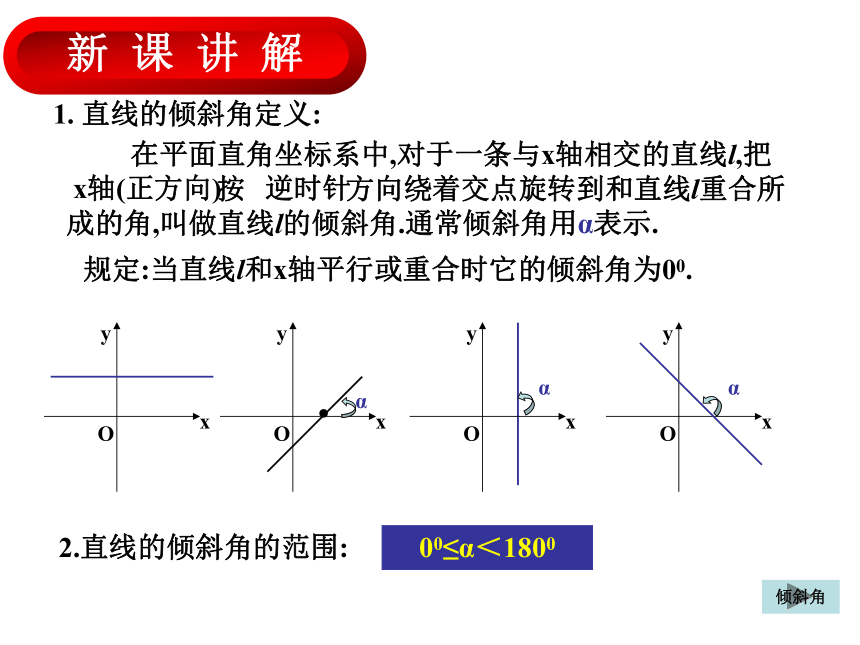
1. 直线的倾斜角定义:
在平面直角坐标系中,对于一条与x轴相交的直线l,把
按 方向绕着交点旋转到和直线l重合所成的角,叫做直线l的倾斜角.通常倾斜角用α表示.
规定:当直线l和x轴平行或重合时它的倾斜角为00.
O
x
y
O
x
y
.
α
O
x
y
α
O
x
y
α
x轴(正方向)
逆时针
2.直线的倾斜角的范围:
00≤α<1800
倾斜角
新 课 讲 解
3.直线倾斜角的意义
1)体现了直线对x轴正方向的倾斜程度;
2)在平面直角坐标系中,每一条直线都有一个确定的倾斜角。
求下列图中 直线的倾斜角是多少度
练习1
1200
y
x
O
l2
l1
l1⊥l2
1500
A
B
D
C
600
4.坡度与坡角
坡度刻画了道路的倾斜程度
n
m
o
P
坡度=
o
P
1
坡度=
1
斜坡
平面直角坐标系中的直线
直线的倾斜角
直线的斜率
坡角
坡度
x
y
l2
O
n
5.过原点的直线的斜率
(1)00≤α<900的直线的斜率
(2)900<α<1800的直线的斜率
P(1,-n)
A(1,0)
m
1
A(1,0)
P(1,m)
x
y
O
l1
α
1
α
当横坐标x从0到1增加一个单位时,纵坐标y从0增加到m(m≥0),
称m为这直线的斜率.
tanα=m
当横坐标x从0到1增加一个单位时,纵坐标y从0减少了n(n>0),
称-n为这直线的斜率.
tanα=-n
通常我们把直线倾斜角的正切值叫做直线的斜率
k=tanα(α≠900)
倾斜角为900的直线的斜率不存在.
6.不过原点直线的斜率
直线l与l1平行(与x轴不垂直),则直线l的斜率k=tanα.
倾斜角α=900的直线的斜率不存在.
900<α<1800
l1
α
x
y
O
00≤α<900
l
x
y
l1
O
α
l
问题1 α=00时,斜率k等于多少
k=tan00=0
k=tan α>0
k=tan α<0
问题3 900<α<1800时,斜率k是正还是负
倾斜角α变化时,直线的斜率k如何变化
倾斜角越大,斜率也越大.
倾斜角越大,斜率也越大.
问题2 00<α<900时,斜率k是正还是负
倾斜角α变化时,直线的斜率k如何变化
倾斜角与斜率
思考交流
p
o
y
x
p
o
y
x
p
o
y
x
y
p
o
x
直线的倾斜角为锐角,k>0; 随着直线的倾斜角增大,k值增大。
--斜率与倾斜角的变化关系
直线的倾斜角为钝角, k<0 ; 随着直线的倾斜角增大,k值增大。
垂直于x轴的直线的倾斜角为90°,但其斜率不存在。
直线平行于x轴或与x轴重合,此时直线的倾斜角为0°, k=0。
练习2
③直线的倾斜角越大,它的斜率也越大( )
②平行于x轴的直线的倾斜角是00或1800.( )
①所有直线都有倾斜角,所有的直线都有斜率( )
×
×
×
(1)判断下列命题是否正确。
(2)直线l1, l2, l3的斜率分别为k1 ,k2 ,k3,试比较它们斜率的大小.
k2>k3>0>k1
l1
l2
l3
y
x
O
如图,当α为锐角时,
锐角
--由两点确定直线的斜率
如图,当α为钝角时,
钝角
--由两点确定直线的斜率
x
O
y
7.过两点的直线的斜率公式
l
在直线l上任取不同的两点
P1(x1,y1),P2(x2,y2)(其中x1≠x2).
过两点的直线的斜率公式为:
验证两点任意性
P1(x1,y1)
P2(x2,y2)
练习3:
求经过下列两点直线的斜率,并判断倾斜角是锐角还是钝角。
(1)A(3,2),B(-4,1)
(2)A(3,2),B(4,1)
(3)A(3,2),B(3,-1)
(4)A(3,2),B(-4,2)
(3)不存在
练习4
求:过点M(2,1),N(m,2)(m∈R)直线MN的斜率.
解:
当m=2时,直线MN与x轴垂直,
当m≠2时,直线MN的斜率:
∴直线MN的斜率不存在;
k=
本节课主要内容:
1.直线的倾斜角的定义;
2.直线的倾斜角与斜率的关系;
3.过两点的直线的斜率公式及其运用.
归纳小结
作业布置
例 已知直线l经过点P(1,1),且与线段MN相交,又M(2,-3),
N(-3,-2),求直线l的斜率k的取值范围.
解 直线l 相当于绕着P在直线PM与PN
间旋转,
当l由PN位置旋转到l1位置时,倾斜
角增大到900,
而kPN=
又当l从直线PM旋转到l1时,倾斜角减少到900,
而kPM=-4
综上所述,
y
x
-3
-2
-1
O
3
2
1
1
-1
-2
N(-3,-2)
M(2,-3)
P(1,1)
l1是 过P点且垂直于x轴的直线.
l1
PN旋转
:
深化拓展
o
直线的倾斜角和斜率
在直角坐标系中如何确定直线的位置呢?
.
Q
.
P
O
x
y
问题探究
方法一:两点确定一条直线
P
y
o
x
.
问题1:过定点P的直线有几条?
问题2:与x轴正方向形成45度角的直线有几条?
y
o
x
P
y
o
x
.
问题3:过点P,与x轴正方向形成45度角的直线有几条?
而直线的方向我们就是用倾斜角来刻画的。
总 结 归 纳
在平面直角坐标系中,确定一条直线位置确定的几何条件是:已知直线上的一个点和这条直线的方向。
P
y
o
x
.
我们把 和 角就叫做直线 与 的倾斜角。
1. 直线的倾斜角定义:
在平面直角坐标系中,对于一条与x轴相交的直线l,把
按 方向绕着交点旋转到和直线l重合所成的角,叫做直线l的倾斜角.通常倾斜角用α表示.
规定:当直线l和x轴平行或重合时它的倾斜角为00.
O
x
y
O
x
y
.
α
O
x
y
α
O
x
y
α
x轴(正方向)
逆时针
2.直线的倾斜角的范围:
00≤α<1800
倾斜角
新 课 讲 解
3.直线倾斜角的意义
1)体现了直线对x轴正方向的倾斜程度;
2)在平面直角坐标系中,每一条直线都有一个确定的倾斜角。
求下列图中 直线的倾斜角是多少度
练习1
1200
y
x
O
l2
l1
l1⊥l2
1500
A
B
D
C
600
4.坡度与坡角
坡度刻画了道路的倾斜程度
n
m
o
P
坡度=
o
P
1
坡度=
1
斜坡
平面直角坐标系中的直线
直线的倾斜角
直线的斜率
坡角
坡度
x
y
l2
O
n
5.过原点的直线的斜率
(1)00≤α<900的直线的斜率
(2)900<α<1800的直线的斜率
P(1,-n)
A(1,0)
m
1
A(1,0)
P(1,m)
x
y
O
l1
α
1
α
当横坐标x从0到1增加一个单位时,纵坐标y从0增加到m(m≥0),
称m为这直线的斜率.
tanα=m
当横坐标x从0到1增加一个单位时,纵坐标y从0减少了n(n>0),
称-n为这直线的斜率.
tanα=-n
通常我们把直线倾斜角的正切值叫做直线的斜率
k=tanα(α≠900)
倾斜角为900的直线的斜率不存在.
6.不过原点直线的斜率
直线l与l1平行(与x轴不垂直),则直线l的斜率k=tanα.
倾斜角α=900的直线的斜率不存在.
900<α<1800
l1
α
x
y
O
00≤α<900
l
x
y
l1
O
α
l
问题1 α=00时,斜率k等于多少
k=tan00=0
k=tan α>0
k=tan α<0
问题3 900<α<1800时,斜率k是正还是负
倾斜角α变化时,直线的斜率k如何变化
倾斜角越大,斜率也越大.
倾斜角越大,斜率也越大.
问题2 00<α<900时,斜率k是正还是负
倾斜角α变化时,直线的斜率k如何变化
倾斜角与斜率
思考交流
p
o
y
x
p
o
y
x
p
o
y
x
y
p
o
x
直线的倾斜角为锐角,k>0; 随着直线的倾斜角增大,k值增大。
--斜率与倾斜角的变化关系
直线的倾斜角为钝角, k<0 ; 随着直线的倾斜角增大,k值增大。
垂直于x轴的直线的倾斜角为90°,但其斜率不存在。
直线平行于x轴或与x轴重合,此时直线的倾斜角为0°, k=0。
练习2
③直线的倾斜角越大,它的斜率也越大( )
②平行于x轴的直线的倾斜角是00或1800.( )
①所有直线都有倾斜角,所有的直线都有斜率( )
×
×
×
(1)判断下列命题是否正确。
(2)直线l1, l2, l3的斜率分别为k1 ,k2 ,k3,试比较它们斜率的大小.
k2>k3>0>k1
l1
l2
l3
y
x
O
如图,当α为锐角时,
锐角
--由两点确定直线的斜率
如图,当α为钝角时,
钝角
--由两点确定直线的斜率
x
O
y
7.过两点的直线的斜率公式
l
在直线l上任取不同的两点
P1(x1,y1),P2(x2,y2)(其中x1≠x2).
过两点的直线的斜率公式为:
验证两点任意性
P1(x1,y1)
P2(x2,y2)
练习3:
求经过下列两点直线的斜率,并判断倾斜角是锐角还是钝角。
(1)A(3,2),B(-4,1)
(2)A(3,2),B(4,1)
(3)A(3,2),B(3,-1)
(4)A(3,2),B(-4,2)
(3)不存在
练习4
求:过点M(2,1),N(m,2)(m∈R)直线MN的斜率.
解:
当m=2时,直线MN与x轴垂直,
当m≠2时,直线MN的斜率:
∴直线MN的斜率不存在;
k=
本节课主要内容:
1.直线的倾斜角的定义;
2.直线的倾斜角与斜率的关系;
3.过两点的直线的斜率公式及其运用.
归纳小结
作业布置
例 已知直线l经过点P(1,1),且与线段MN相交,又M(2,-3),
N(-3,-2),求直线l的斜率k的取值范围.
解 直线l 相当于绕着P在直线PM与PN
间旋转,
当l由PN位置旋转到l1位置时,倾斜
角增大到900,
而kPN=
又当l从直线PM旋转到l1时,倾斜角减少到900,
而kPM=-4
综上所述,
y
x
-3
-2
-1
O
3
2
1
1
-1
-2
N(-3,-2)
M(2,-3)
P(1,1)
l1是 过P点且垂直于x轴的直线.
l1
PN旋转
:
深化拓展
