圆与圆的位置关系

(共11张PPT)
圆与圆的位置关系
一.复习提问
提问：已知直线和圆请同学们想想我们怎么样来确定直线和圆的位置关系？
图1 图2 图3
名称
几何关系
方程组
公共点
直线L
图1
图2
图3
相离
d ＞r
无解
0
相切
d ＝r
一解
1
切线
相交
d ＜r
两解
2
割线
二.新课导入
太阳
月亮
月亮
月亮
月亮
月亮
月亮
月亮
月亮
月亮
月亮
请同学们观看罕见的日全食发生的全过程!
设想：如果把月亮与太阳看成同一平面内的两个圆，那么两个圆在作相对运动的过程中有几种位置关系产生呢？
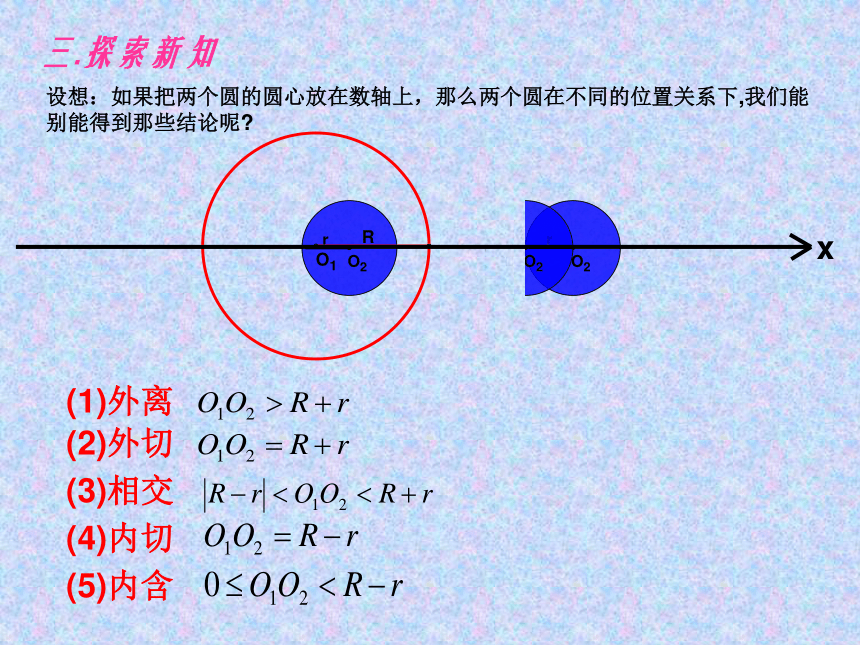
三.探索新知
设想：如果把两个圆的圆心放在数轴上，那么两个圆在不同的位置关系下,我们能
别能得到那些结论呢
(1)外离
(2)外切
(3)相交
(4)内切
(5)内含
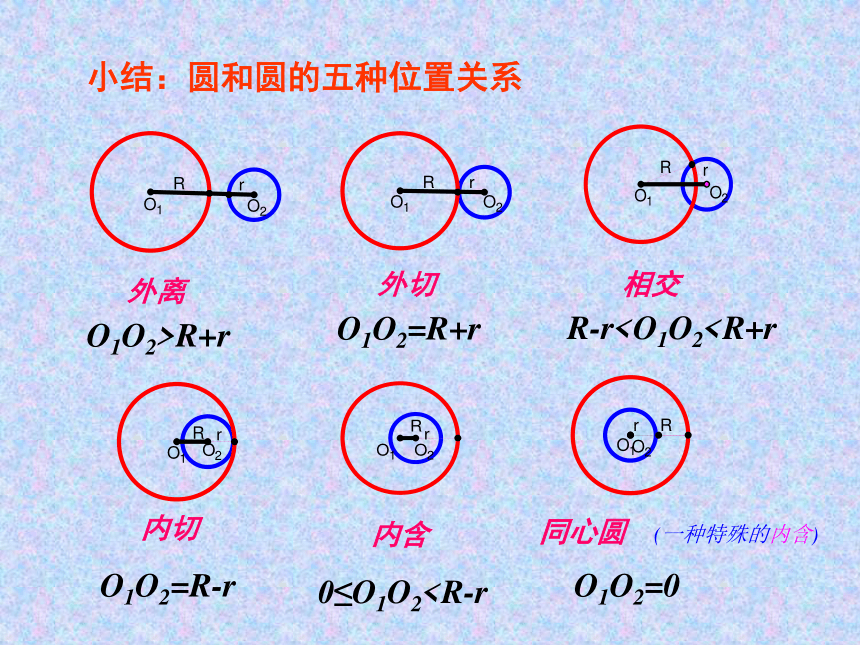
小结：圆和圆的五种位置关系
外离
O1O2>R+r
O1O2=R+r
外切
相交
R-r内切
O1O2=R-r
内含
0≤O1O2同心圆
O1O2=0
(一种特殊的内含)
四．例题讲解
例1：判断下列两圆的位置关系：
（1）
（2）
分析：要判断两圆的位置关系，关键是找到圆心距和两圆半径的数量关系。
所以两圆外切。
因为
解（2）：将两圆的方程化成标准方程，得
故两圆的半径分别为 ，两圆的圆心距
因为
所以两圆相交 .
解（1）：根据题意得，两圆的半径分别为 ，两圆的圆心距
o
例2：求过点A(0,6)且与圆C: 切与原点的圆方程。
分析：如图，所求圆经过原点和点A(0,6),且圆心必在已知圆的圆心和切点的连线上，根据这三个条件可确定圆的方程。
将圆C化为标准方程，得
则圆心为C(-5,-5),半径为 ，
所以经过已知圆的圆心和切点的直线方程为 。
由题意知，O(0,0),A(0,6)在所求圆上，且圆心在直线上 ，
则有
解：设所求圆的方程为
解得
所以所求圆的方程为： 。
A(0,6)
五.能 力 拓 展
1、 求点A(1,2)之距为1，且点B(3,1)之距为2的直线共有 条。
2
分析：因为到A点距离为1的直线都是以A为圆心，以1半径的圆的切线，到B点距离为2的直线都是以B圆心，以2半径的圆的切线，所以本题就转化为求两圆的公切线条数，因为两圆相交，显然，满足题意的直线有2条。
作法:
1.取A(1,2)再以以A为圆心，以1为半径作圆A.
2.取B(3,1)再以以B为圆心，以3为半径作圆B.
３. 作圆A和圆B的公切线.
显然：有两解．
课堂练习：
１,若圆　　　　　　　　　　　　　　　　　　　　　　　　　　相交，求实数m的范围 　　　。
2、已知以C(-4,3)为圆心的圆与圆 相切，求圆C的方程。
作业:P107习题2.2(2) 1至5题.
1解得:
外切
内切
课堂小结:
相离
外切
相交
内切
内含
0
1
2
1
0
d>R+r
d=R+r
R-rd=R-r
d公共点
圆心距和半径的关系
两圆位置
一圆在另一
圆的外部
一圆在另一
圆的外部
两圆相交
一圆在另一
圆的内部
一圆在另一
圆的内部
名称