12.3.1等腰三角形(2)
文档属性
| 名称 | 12.3.1等腰三角形(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 448.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-08 00:00:00 | ||
图片预览




文档简介
(共31张PPT)
等腰三角形的判定
等腰三角形的判定
等腰三角形的判定
如图所示,量出AC的长,就可知道河的宽度AB。你知道为什么吗?
30°
60°
B
A
C
A
B
O
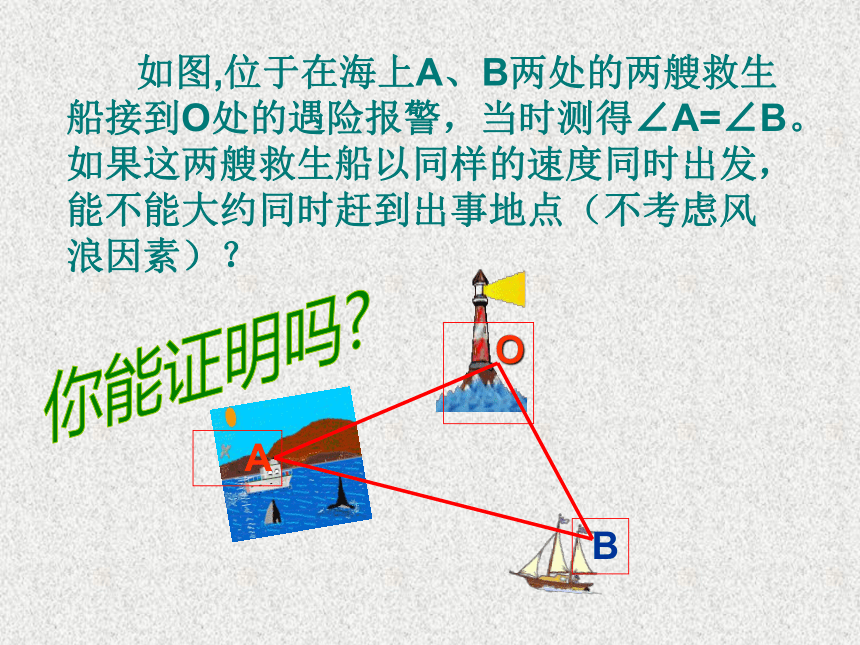
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
我们在上一节学习了等腰三角形的性质。现在你能回答我一些问题吗?
温故而知新
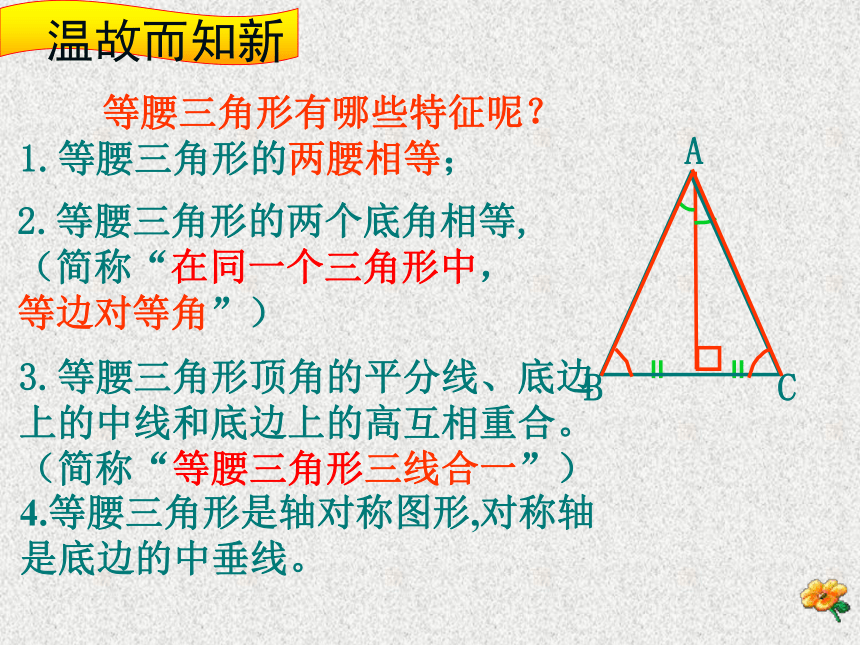
1.等腰三角形的两腰相等;
等腰三角形有哪些特征呢?
A
B
C
2.等腰三角形的两个底角相等,(简称“在同一个三角形中,等边对等角”)
3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合。(简称“等腰三角形三线合一”)
4.等腰三角形是轴对称图形,对称轴是底边的中垂线。
温故而知新
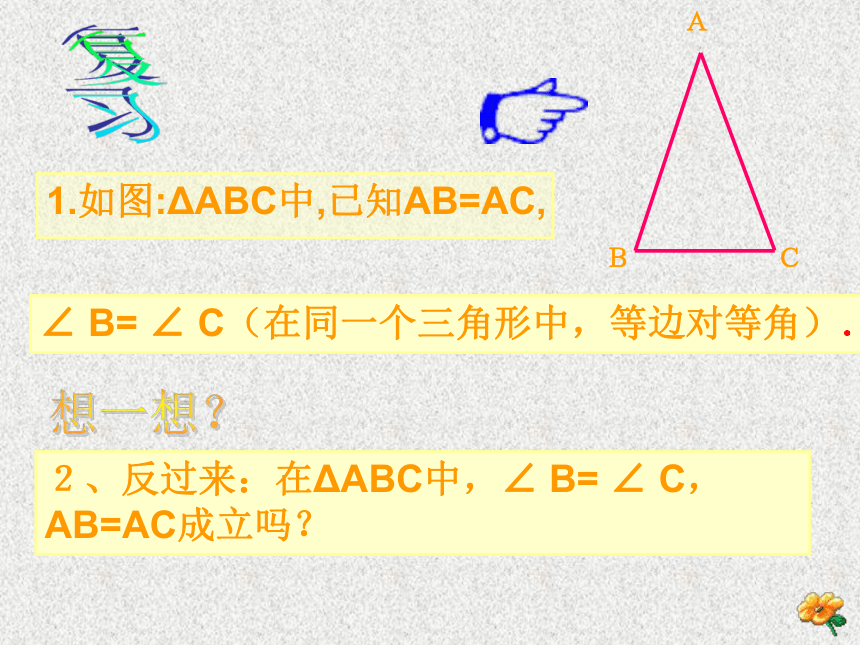
1.如图:ΔABC中,已知AB=AC,
∠ B= ∠ C(在同一个三角形中,等边对等角).
2、反过来:在ΔABC中,∠ B= ∠ C, AB=AC成立吗?
A
B
C
探索思考
1,作一个三角形,有两个角相等,这两个角所对的边是否相等?
A
B
C
D
图中有哪些角相等
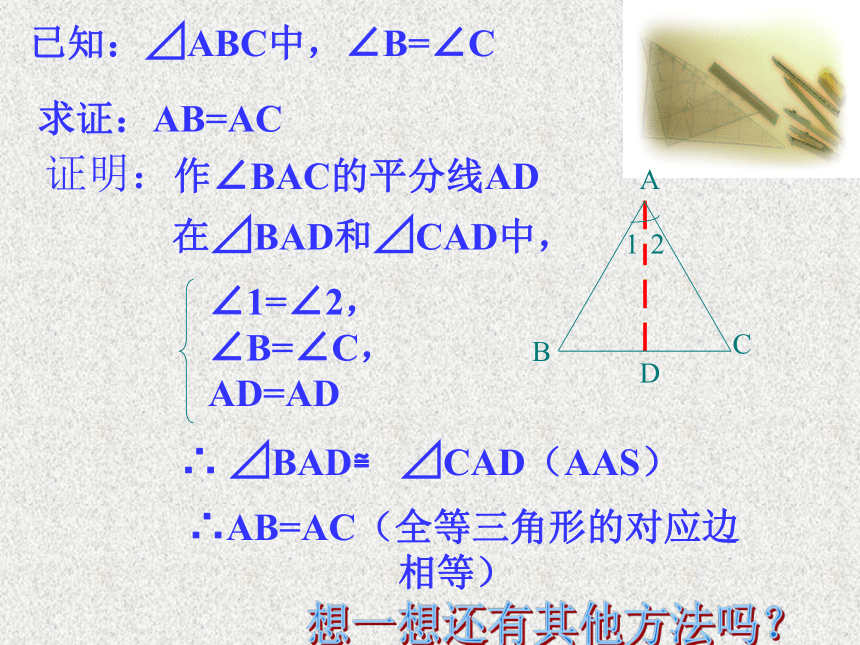
已知:⊿ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
已知
等角对等边
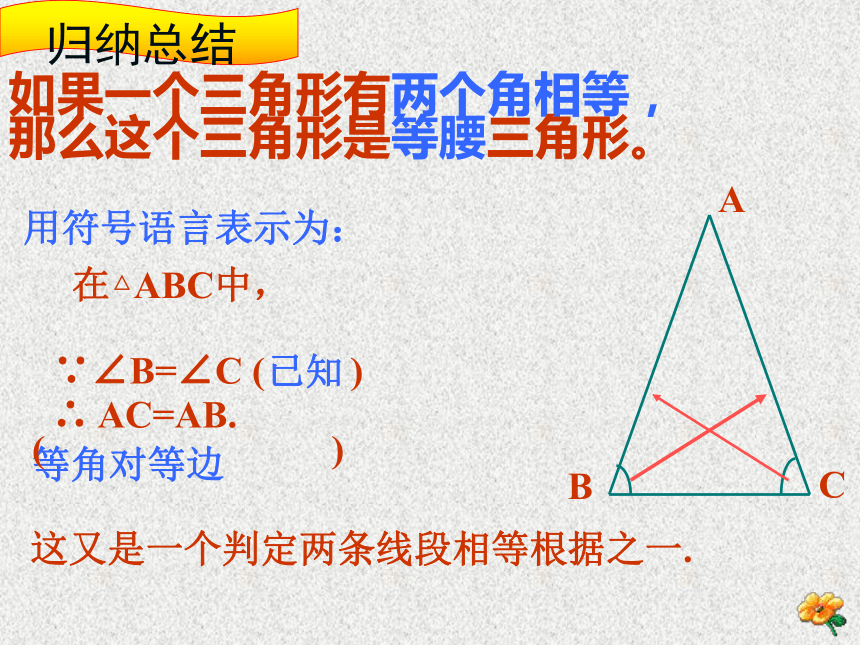
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
在△ABC中,
A
B
C
∵∠B=∠C ( )
∴ AC=AB. ( )
用符号语言表示为:
这又是一个判定两条线段相等根据之一.
归纳总结
问:如图,下列推理正确吗
A
B
C
D
2
1
∵∠1=∠2 ∴ BD=DC
(等角对等边)
∵∠1=∠2 ∴ DC=BC
A
B
C
D
2
1
(等角对等边)
错,因为都不是在同一个三角形中。
在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
练一练
解:等腰三角形;在△ABC中
∵ ∠A=40°,∠B=70°,
∴ ∠C= 180°-70°- 40° =70°
∴ ∠B=∠C, ∴ AB=AC
C
B
A
D
1
2
已知:如图, ∠A= ∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
练一练
解:
∠1=720 ∠2=360
等腰三角形有: ⊿ABC, ⊿ABD,⊿BCD
C
B
A
D
1
2
练习2
B
A
D
C
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
B
A
D
C
证明: ∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD
如图所示,量出AC的长,就可知道河的宽度AB。你知道为什么吗?
30°
60°
B
A
C
解: 如图∵ ∠ DAC= 60 ° ∠ C= 30 °
∠ DAC= ∠ B+ ∠ C
∴ ∠ B= ∠ DAC -∠ C
=60 °- 30 ° =30 °
∴ ∠ B= ∠ C
∴ AB=AC(在同一个三角形中, 等角对等边)
即AC的长就是河宽。
三、范例讲解:
生活实例:一次数学实践活动的内容是测量河宽,如图,即测量A, B之间的距离。小明想出了一个方法:从点A出发,沿着与直线AB成60 °角的AC方向前进至C , 在C处测得∠ C= 30 °,量出AC的长,它就是河的宽度。这个方法正确吗?请说明理由。
30 °
A
B
C
D
60 °
A
B
O
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
例1 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
如图,∠CAE是⊿ABC的外角,∠1=∠2,
AD∥BC。
求证:AB=AC
分析:
从求证看:要证AB=AC,需证∠B=∠C,
从已知看:因为∠1=∠2,AD∥BC
可以找出∠B,∠C与的关系。
已知:
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角)。
A
B
C
D
E
1
2
例2:如图,BD是等腰三角形ABC的底边AC上的
交AB于点E, 问:图中共有几对
高,DE∥BC,
等腰三角形,请说说理由.
A
B
C
D
E
思考探究:在△ABC中,已知 AB =AC ,BO平分∠ABC,CO平分∠ACB.过点O作直线EF//BC交AB于E,交AC于F.
(1)请问图中有多少个等腰三角形 说明理由.
(2)线段EF和线段EB,FC之间有没有关系 若有,是什么关系
F
E
0
B
C
A
AB≠AC
B
0
C
A
E
F
思考探索
已知:如图,在△ABC中,BD、CD分别平分∠ABC、∠ACE并交于点D,过F作 DF∥BE
则线段FG,BF,CG之间又会有什么关系?若有请写出关系式,并说明理由。
开启 智慧
已知:如图,在△ABC中,BF、CF分别平分∠DBC、∠ECB并交于点F,过F作 DE∥BC
求证:DE=BD+CE
开启 智慧
已知:如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB并交于点O,过点O作 OD∥AB, OE∥AC,BC=16,
求: △ODE的周长
试一试
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形。
2.等边对等角,
3. 三线合一。
4.是轴对称图形.
2.等角对等边,
1.两边相等。
1.两腰相等.
小结
2、等腰三角形的判定方法有下列几种: 。
4、等腰三角形的判定定理与性质定理的区别是 。
5、运用等腰三角形的判定定理时,应注意 。
1、等腰三角形的判定定理
①定义,②判定定理
条件和结论刚好相反。
在同一个三角形中
1.课本53页练习第3题
2.课本56页习题第2题、第5题
3.《打好基础》
等腰三角形的判定
等腰三角形的判定
等腰三角形的判定
如图所示,量出AC的长,就可知道河的宽度AB。你知道为什么吗?
30°
60°
B
A
C
A
B
O
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
我们在上一节学习了等腰三角形的性质。现在你能回答我一些问题吗?
温故而知新
1.等腰三角形的两腰相等;
等腰三角形有哪些特征呢?
A
B
C
2.等腰三角形的两个底角相等,(简称“在同一个三角形中,等边对等角”)
3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合。(简称“等腰三角形三线合一”)
4.等腰三角形是轴对称图形,对称轴是底边的中垂线。
温故而知新
1.如图:ΔABC中,已知AB=AC,
∠ B= ∠ C(在同一个三角形中,等边对等角).
2、反过来:在ΔABC中,∠ B= ∠ C, AB=AC成立吗?
A
B
C
探索思考
1,作一个三角形,有两个角相等,这两个角所对的边是否相等?
A
B
C
D
图中有哪些角相等
已知:⊿ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
已知
等角对等边
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
在△ABC中,
A
B
C
∵∠B=∠C ( )
∴ AC=AB. ( )
用符号语言表示为:
这又是一个判定两条线段相等根据之一.
归纳总结
问:如图,下列推理正确吗
A
B
C
D
2
1
∵∠1=∠2 ∴ BD=DC
(等角对等边)
∵∠1=∠2 ∴ DC=BC
A
B
C
D
2
1
(等角对等边)
错,因为都不是在同一个三角形中。
在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
练一练
解:等腰三角形;在△ABC中
∵ ∠A=40°,∠B=70°,
∴ ∠C= 180°-70°- 40° =70°
∴ ∠B=∠C, ∴ AB=AC
C
B
A
D
1
2
已知:如图, ∠A= ∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
练一练
解:
∠1=720 ∠2=360
等腰三角形有: ⊿ABC, ⊿ABD,⊿BCD
C
B
A
D
1
2
练习2
B
A
D
C
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
B
A
D
C
证明: ∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD
如图所示,量出AC的长,就可知道河的宽度AB。你知道为什么吗?
30°
60°
B
A
C
解: 如图∵ ∠ DAC= 60 ° ∠ C= 30 °
∠ DAC= ∠ B+ ∠ C
∴ ∠ B= ∠ DAC -∠ C
=60 °- 30 ° =30 °
∴ ∠ B= ∠ C
∴ AB=AC(在同一个三角形中, 等角对等边)
即AC的长就是河宽。
三、范例讲解:
生活实例:一次数学实践活动的内容是测量河宽,如图,即测量A, B之间的距离。小明想出了一个方法:从点A出发,沿着与直线AB成60 °角的AC方向前进至C , 在C处测得∠ C= 30 °,量出AC的长,它就是河的宽度。这个方法正确吗?请说明理由。
30 °
A
B
C
D
60 °
A
B
O
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
例1 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
如图,∠CAE是⊿ABC的外角,∠1=∠2,
AD∥BC。
求证:AB=AC
分析:
从求证看:要证AB=AC,需证∠B=∠C,
从已知看:因为∠1=∠2,AD∥BC
可以找出∠B,∠C与的关系。
已知:
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角)。
A
B
C
D
E
1
2
例2:如图,BD是等腰三角形ABC的底边AC上的
交AB于点E, 问:图中共有几对
高,DE∥BC,
等腰三角形,请说说理由.
A
B
C
D
E
思考探究:在△ABC中,已知 AB =AC ,BO平分∠ABC,CO平分∠ACB.过点O作直线EF//BC交AB于E,交AC于F.
(1)请问图中有多少个等腰三角形 说明理由.
(2)线段EF和线段EB,FC之间有没有关系 若有,是什么关系
F
E
0
B
C
A
AB≠AC
B
0
C
A
E
F
思考探索
已知:如图,在△ABC中,BD、CD分别平分∠ABC、∠ACE并交于点D,过F作 DF∥BE
则线段FG,BF,CG之间又会有什么关系?若有请写出关系式,并说明理由。
开启 智慧
已知:如图,在△ABC中,BF、CF分别平分∠DBC、∠ECB并交于点F,过F作 DE∥BC
求证:DE=BD+CE
开启 智慧
已知:如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB并交于点O,过点O作 OD∥AB, OE∥AC,BC=16,
求: △ODE的周长
试一试
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形。
2.等边对等角,
3. 三线合一。
4.是轴对称图形.
2.等角对等边,
1.两边相等。
1.两腰相等.
小结
2、等腰三角形的判定方法有下列几种: 。
4、等腰三角形的判定定理与性质定理的区别是 。
5、运用等腰三角形的判定定理时,应注意 。
1、等腰三角形的判定定理
①定义,②判定定理
条件和结论刚好相反。
在同一个三角形中
1.课本53页练习第3题
2.课本56页习题第2题、第5题
3.《打好基础》
