12.3.1等腰三角形(1)
文档属性
| 名称 | 12.3.1等腰三角形(1) |  | |
| 格式 | rar | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-08 21:27:43 | ||
图片预览

文档简介
(共17张PPT)
虞城一中 李建立
12.3.1 等腰三角形
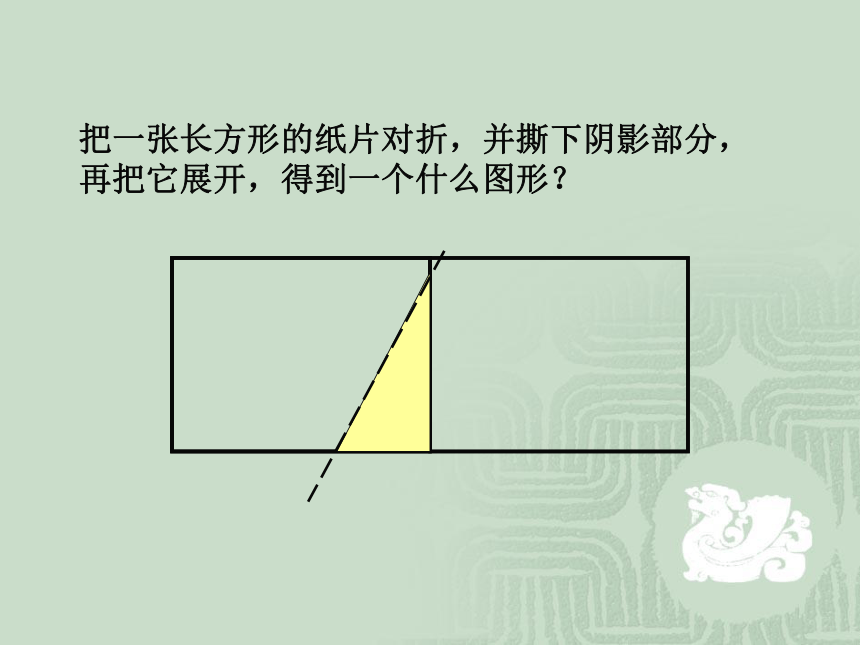
把一张长方形的纸片对折,并撕下阴影部分,再把它展开,得到一个什么图形?
概念就像螺丝钉——微小但非常重要!
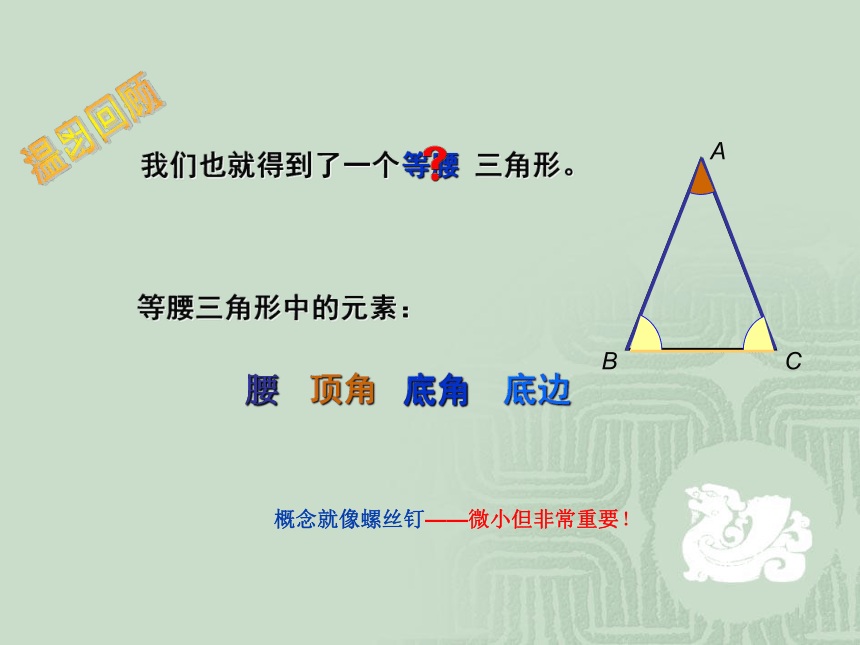
顶角
A
B
C
底边
腰
腰
底角
底角
我们也就得到了一个
等腰
等腰三角形中的元素:
三角形。
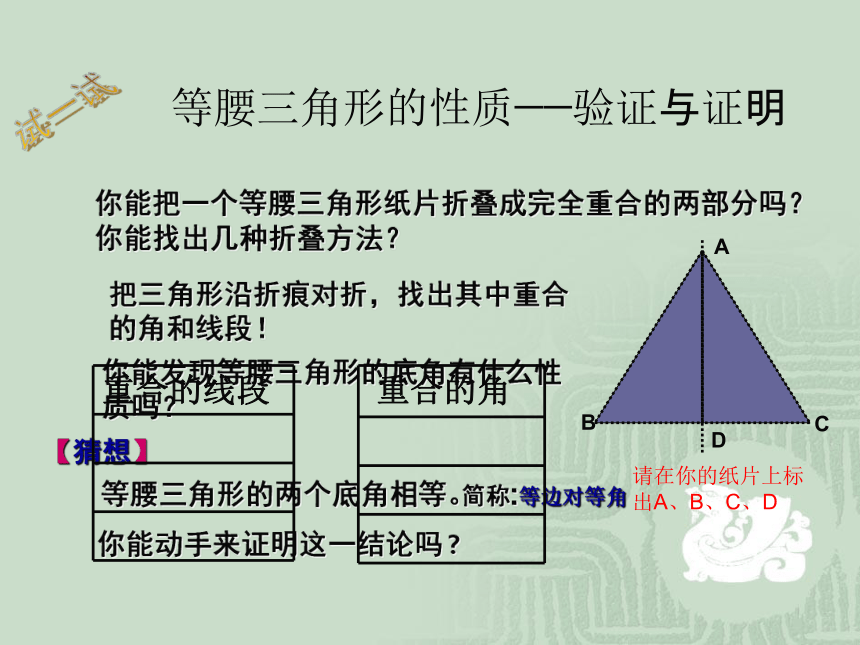
你能把一个等腰三角形纸片折叠成完全重合的两部分吗?
你能找出几种折叠方法?
你能发现等腰三角形的底角有什么性质吗?
A
B
C
D
等腰三角形的两个底角相等。
【猜想】
等腰三角形的性质——验证与证明
你能动手来证明这一结论吗?
简称:等边对等角
把三角形沿折痕对折,找出其中重合的角和线段!
重合的线段
重合的角
请在你的纸片上标
出A、B、C、D
证明
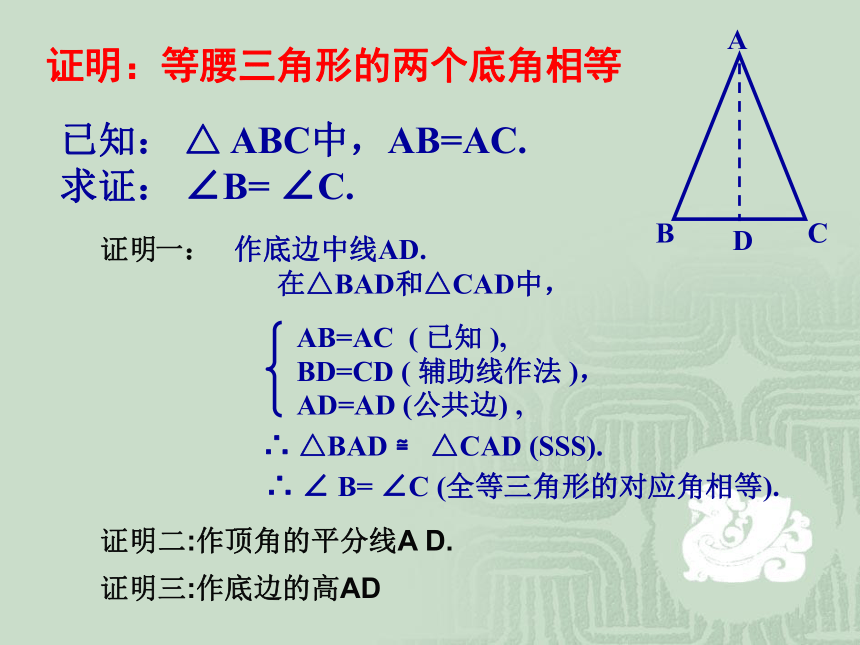
一: 作底边中线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
BD=CD ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
证明二:作顶角的平分线A D.
证明三:作底边的高AD
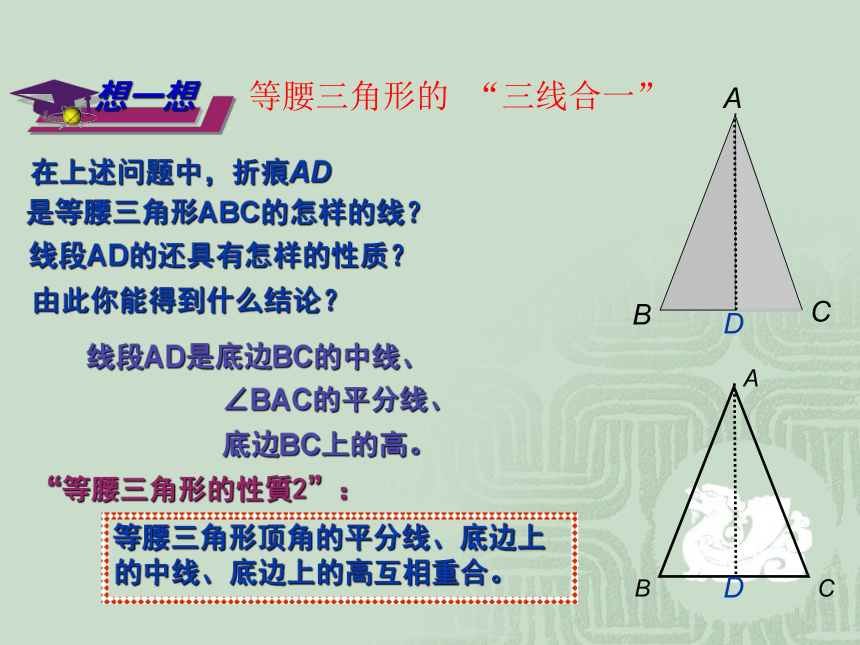
等腰三角形的 “三线合一”
A
B
C
C
B
A
想一想
在上述问题中,折痕AD
D
是等腰三角形ABC的怎样的线?
线段AD的还具有怎样的性质?
D
由此你能得到什么结论?
等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。
“等腰三角形的性質2”:
线段AD是底边BC的中线、
∠BAC的平分线、
底边BC上的高。
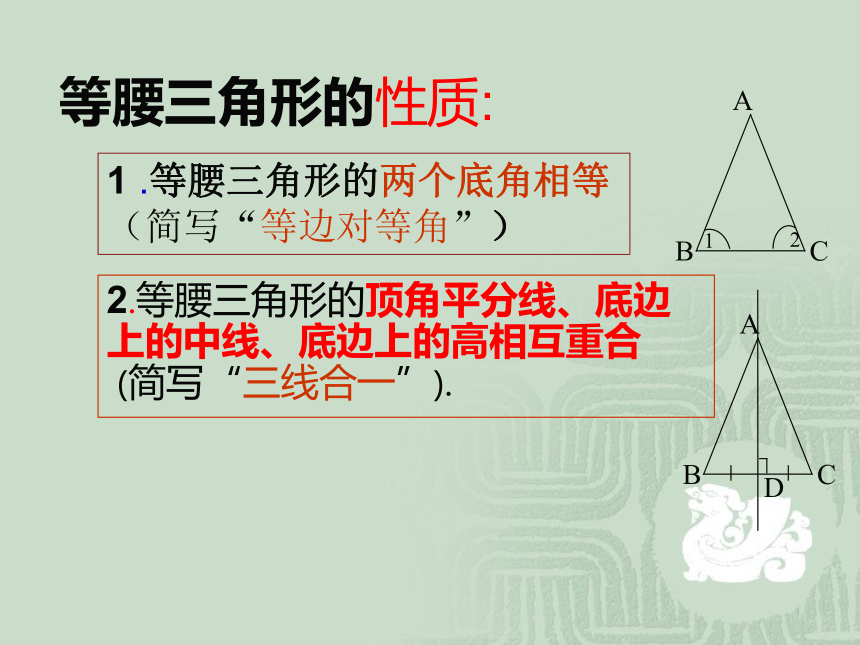
等腰三角形的性质:
2.等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
(简写“三线合一”).
A
C
B
1
2
A
C
B
D
1 .等腰三角形的两个底角相等 (简写“等边对等角”)
等腰三角形的性质1:
等腰三角形的两个底角相等
(简写成“等边对等角”)
注意:
在 等腰三角形中,等边对等角。
一个
一个
用符号语言表示为:
在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )
已知
等边对等角
C
A
B
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。
C
A
B
1
2
D
等腰三角形“三线合一”的性质
用符号语言表示为:
1
2
B D
CD
1
2
AD
BC
AD
BC
B D
CD
问题1 如果等腰三角形的顶角是36 ,那么它的底角的度数是 。
问题2 △ABC中,AB=AC,∠BAC=90 ,AD是BC边上的高,则∠ABD= ,BD=______=______。
A
B
C
D
变式练习 等腰三角形的一个角是 ,那么它的另外两个角的度数是 。
36
110
72 、72
72 、72 或36 、108
35 、35
45°
AD
CD
链接
练习应用、
如图,厂房屋顶钢架外框是等腰三角形,
其中AB=AC,,立柱AD⊥BC.已知∠B=30°, BC=6m,
那么:∠BAC=-----------,BD=-----------
120°
3m
A
B
C
D
例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。
解:∵AB=AC,BC=AD=BD
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)
设∠A=X,则∠BDC=∠A+∠ABD=2X
从而∠ABC=∠C=∠BDC=2X
于是在△ABC中,有∠A+∠ABC+∠C=X+2X+2X=1800
解得 X=360
在△ABC中,∠A=360,∠ABC=∠C=720
如图,在△ABC中,AB=AD=DC,
∠BAD=26°,求∠B和∠C的度数。
B
C
D
A
返回小结
答案
如图,在△ABC中,AB=AD=DC,
∠BAD=26°,求∠B和∠C的度数。
B
C
D
A
解:∵△ABD中, AB=AD
∴∠ABD=∠ADB
又∵ ∠BAD=26°, ∠B+ ∠BAD+ ∠ADB=180°
∴∠B=∠ADB=(180 °-26 °) ÷2=77 °
在△ADC中, AD=DC
∴∠CAD=∠C
又∵ ∠ADB=∠CAD+∠C
即: 2∠C= 77 °
∴∠C=38.5 °
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称等边对等角)
∵AB=AC
∴∠B=∠C
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称三线合一)
∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD
课堂小结
布置作业:
课本第51页1、2、3题.
虞城一中 李建立
12.3.1 等腰三角形
把一张长方形的纸片对折,并撕下阴影部分,再把它展开,得到一个什么图形?
概念就像螺丝钉——微小但非常重要!
顶角
A
B
C
底边
腰
腰
底角
底角
我们也就得到了一个
等腰
等腰三角形中的元素:
三角形。
你能把一个等腰三角形纸片折叠成完全重合的两部分吗?
你能找出几种折叠方法?
你能发现等腰三角形的底角有什么性质吗?
A
B
C
D
等腰三角形的两个底角相等。
【猜想】
等腰三角形的性质——验证与证明
你能动手来证明这一结论吗?
简称:等边对等角
把三角形沿折痕对折,找出其中重合的角和线段!
重合的线段
重合的角
请在你的纸片上标
出A、B、C、D
证明
一: 作底边中线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
BD=CD ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
证明二:作顶角的平分线A D.
证明三:作底边的高AD
等腰三角形的 “三线合一”
A
B
C
C
B
A
想一想
在上述问题中,折痕AD
D
是等腰三角形ABC的怎样的线?
线段AD的还具有怎样的性质?
D
由此你能得到什么结论?
等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。
“等腰三角形的性質2”:
线段AD是底边BC的中线、
∠BAC的平分线、
底边BC上的高。
等腰三角形的性质:
2.等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
(简写“三线合一”).
A
C
B
1
2
A
C
B
D
1 .等腰三角形的两个底角相等 (简写“等边对等角”)
等腰三角形的性质1:
等腰三角形的两个底角相等
(简写成“等边对等角”)
注意:
在 等腰三角形中,等边对等角。
一个
一个
用符号语言表示为:
在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )
已知
等边对等角
C
A
B
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。
C
A
B
1
2
D
等腰三角形“三线合一”的性质
用符号语言表示为:
1
2
B D
CD
1
2
AD
BC
AD
BC
B D
CD
问题1 如果等腰三角形的顶角是36 ,那么它的底角的度数是 。
问题2 △ABC中,AB=AC,∠BAC=90 ,AD是BC边上的高,则∠ABD= ,BD=______=______。
A
B
C
D
变式练习 等腰三角形的一个角是 ,那么它的另外两个角的度数是 。
36
110
72 、72
72 、72 或36 、108
35 、35
45°
AD
CD
链接
练习应用、
如图,厂房屋顶钢架外框是等腰三角形,
其中AB=AC,,立柱AD⊥BC.已知∠B=30°, BC=6m,
那么:∠BAC=-----------,BD=-----------
120°
3m
A
B
C
D
例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。
解:∵AB=AC,BC=AD=BD
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)
设∠A=X,则∠BDC=∠A+∠ABD=2X
从而∠ABC=∠C=∠BDC=2X
于是在△ABC中,有∠A+∠ABC+∠C=X+2X+2X=1800
解得 X=360
在△ABC中,∠A=360,∠ABC=∠C=720
如图,在△ABC中,AB=AD=DC,
∠BAD=26°,求∠B和∠C的度数。
B
C
D
A
返回小结
答案
如图,在△ABC中,AB=AD=DC,
∠BAD=26°,求∠B和∠C的度数。
B
C
D
A
解:∵△ABD中, AB=AD
∴∠ABD=∠ADB
又∵ ∠BAD=26°, ∠B+ ∠BAD+ ∠ADB=180°
∴∠B=∠ADB=(180 °-26 °) ÷2=77 °
在△ADC中, AD=DC
∴∠CAD=∠C
又∵ ∠ADB=∠CAD+∠C
即: 2∠C= 77 °
∴∠C=38.5 °
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称等边对等角)
∵AB=AC
∴∠B=∠C
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称三线合一)
∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD
课堂小结
布置作业:
课本第51页1、2、3题.
