上海市行知中学2021届高三10月月考数学试卷(2020.10) Word版含答案
文档属性
| 名称 | 上海市行知中学2021届高三10月月考数学试卷(2020.10) Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 738.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-24 17:32:22 | ||
图片预览


文档简介
2020-2021学年行知中学高三月考数学试卷2020.10
一. 填空题
1. 已知集合,,则
2. 函数的单调递减区间是
3. 方程的解
4. 函数的反函数是
5. 已知定义在上的函数,满足,且对任意的都有,则
6. 若对任意实数,不等式恒成立,则实数的取值范围是
7. 已知关于的方程有两个实数根,且一根小于,一根大于,则实数的取值
范围为
8. 若函数值域为,则实数的取值范围是
9. 若函数存在零点,则实数的取值范围是
10. 设,若对任意的,都有,则
11. 函数的大致图像如图,若函数图像经过点和点,
且和是其两条渐近线,则
12. 已知函数为偶函数,为奇函数,其中、为常数,
则
二. 选择题
13. 若,,则下列不等式成立的是( )
A. B. C. D.
14. 解析式为,值域为的函数有( )个
A. 4 B. 6 C. 8 D. 9
15. 定义在上的函数满足,且当时,单调递增,若,,则的值( )
A. 恒为负值 B. 恒等于零 C. 恒为正值 D. 无法确定正负
16. 若存在与正数,使成立,则称“函数在处存在距离为的对称点”,
设,若对于任意,总存在正数,使得“函数在处存在距离为
的对称点”,则实数的取值范围是( )
A. B. C. D.
三. 解答题
17. 若在上的最大值为2.
求的值;
求不等式的解集.
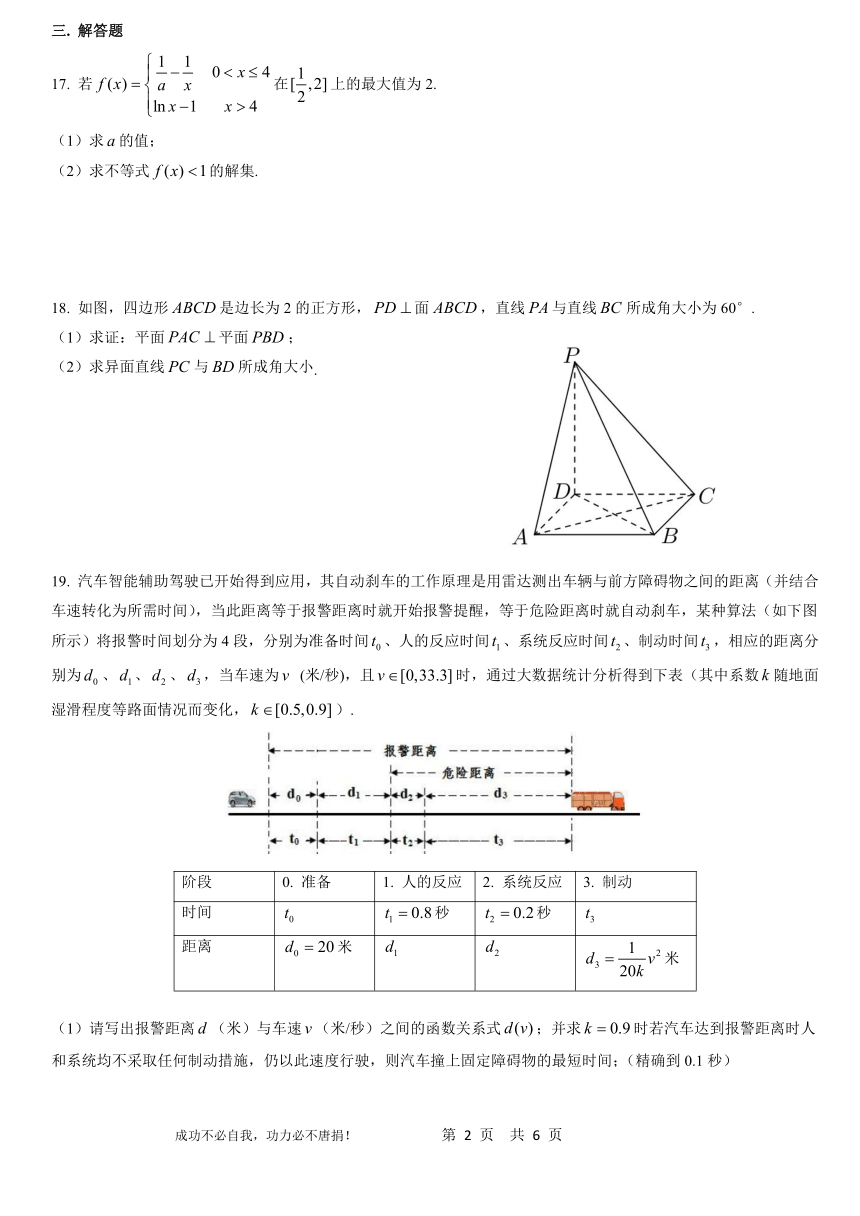
18. 如图,四边形是边长为2的正方形,面,直线与直线所成角大小为60°.
(1)求证:平面平面;
(2)求异面直线与所成角大小.
19. 汽车智能辅助驾驶已开始得到应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车,某种算法(如下图所示)将报警时间划分为4段,分别为准备时间、人的反应时间、系统反应时间、制动时间,相应的距离分别为、、、,当车速为 (米/秒),且时,通过大数据统计分析得到下表(其中系数随地面湿滑程度等路面情况而变化,).
阶段 0. 准备 1. 人的反应 2. 系统反应 3. 制动
时间
秒 秒
距离 米
米
(1)请写出报警距离(米)与车速(米/秒)之间的函数关系式;并求时若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间;(精确到0.1秒)
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80米,则汽车的行驶速度应限制在多少米/秒以下?
20. 定义在上的函数,如果对任意,恒有(,)成立,则称为阶缩放函数.
(1)已知为二阶缩放函数,且当时,,求的值;
(2)已知函数为二阶缩放函数,且当时,,判断函数在上有
无零点;
(3)已知函数为阶缩放函数,且当时,的取值范围是,求在()
上的取值范围.
21. 已知为奇函数.
(1)求、、的值;
(2)若,,且,求的值;
(3)若对于任意的,函数、满足,则称在上与具有“H类关系”,问函数与函数在上是否具有“H类关系”,请说明理由.
2020-2021学年行知中学高三月考数学试卷参考答案
一. 填空题
1. 2. 或 3. 1 4.
5. 6. 或 7. 8.
9. 10. 3 11. 12.
二. 选择题 13. C 14. D 15. A 16. C
三. 解答题
17.(1)∵在上单调递增,∴,计算得:;(说明:无指出单调性扣3分)
当时,;
当时,,
综上:不等式的解集为.
18.(1)证明:∵面,∵,又∵,∴,
∵面,∴平面平面;
(2)设正方形的中心为,中点为,则∥,
∴(或其补角)是异面直线与所成角,∵,∴,,
又,∴,,∴,
∴直线与直线所成角大小为.
20.(1);
(2)当时,,
则,
令,解得:或均不在内,
∴函数在上无零点;
(3)当时,的取值范围是且,
∴当时,,∵,∴,
∴当时,,
∵,∴在()上的取值范围为.
21.(1)为奇函数,,,,
综上:,,;
设,为奇函数为奇函数,
,;
(3)
在上单调递增,
,
即,f(x)与g(x)具有“H类关系”.
成功不必自我,功力必不唐捐! 第 6 页 共 6 页
一. 填空题
1. 已知集合,,则
2. 函数的单调递减区间是
3. 方程的解
4. 函数的反函数是
5. 已知定义在上的函数,满足,且对任意的都有,则
6. 若对任意实数,不等式恒成立,则实数的取值范围是
7. 已知关于的方程有两个实数根,且一根小于,一根大于,则实数的取值
范围为
8. 若函数值域为,则实数的取值范围是
9. 若函数存在零点,则实数的取值范围是
10. 设,若对任意的,都有,则
11. 函数的大致图像如图,若函数图像经过点和点,
且和是其两条渐近线,则
12. 已知函数为偶函数,为奇函数,其中、为常数,
则
二. 选择题
13. 若,,则下列不等式成立的是( )
A. B. C. D.
14. 解析式为,值域为的函数有( )个
A. 4 B. 6 C. 8 D. 9
15. 定义在上的函数满足,且当时,单调递增,若,,则的值( )
A. 恒为负值 B. 恒等于零 C. 恒为正值 D. 无法确定正负
16. 若存在与正数,使成立,则称“函数在处存在距离为的对称点”,
设,若对于任意,总存在正数,使得“函数在处存在距离为
的对称点”,则实数的取值范围是( )
A. B. C. D.
三. 解答题
17. 若在上的最大值为2.
求的值;
求不等式的解集.
18. 如图,四边形是边长为2的正方形,面,直线与直线所成角大小为60°.
(1)求证:平面平面;
(2)求异面直线与所成角大小.
19. 汽车智能辅助驾驶已开始得到应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车,某种算法(如下图所示)将报警时间划分为4段,分别为准备时间、人的反应时间、系统反应时间、制动时间,相应的距离分别为、、、,当车速为 (米/秒),且时,通过大数据统计分析得到下表(其中系数随地面湿滑程度等路面情况而变化,).
阶段 0. 准备 1. 人的反应 2. 系统反应 3. 制动
时间
秒 秒
距离 米
米
(1)请写出报警距离(米)与车速(米/秒)之间的函数关系式;并求时若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间;(精确到0.1秒)
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80米,则汽车的行驶速度应限制在多少米/秒以下?
20. 定义在上的函数,如果对任意,恒有(,)成立,则称为阶缩放函数.
(1)已知为二阶缩放函数,且当时,,求的值;
(2)已知函数为二阶缩放函数,且当时,,判断函数在上有
无零点;
(3)已知函数为阶缩放函数,且当时,的取值范围是,求在()
上的取值范围.
21. 已知为奇函数.
(1)求、、的值;
(2)若,,且,求的值;
(3)若对于任意的,函数、满足,则称在上与具有“H类关系”,问函数与函数在上是否具有“H类关系”,请说明理由.
2020-2021学年行知中学高三月考数学试卷参考答案
一. 填空题
1. 2. 或 3. 1 4.
5. 6. 或 7. 8.
9. 10. 3 11. 12.
二. 选择题 13. C 14. D 15. A 16. C
三. 解答题
17.(1)∵在上单调递增,∴,计算得:;(说明:无指出单调性扣3分)
当时,;
当时,,
综上:不等式的解集为.
18.(1)证明:∵面,∵,又∵,∴,
∵面,∴平面平面;
(2)设正方形的中心为,中点为,则∥,
∴(或其补角)是异面直线与所成角,∵,∴,,
又,∴,,∴,
∴直线与直线所成角大小为.
20.(1);
(2)当时,,
则,
令,解得:或均不在内,
∴函数在上无零点;
(3)当时,的取值范围是且,
∴当时,,∵,∴,
∴当时,,
∵,∴在()上的取值范围为.
21.(1)为奇函数,,,,
综上:,,;
设,为奇函数为奇函数,
,;
(3)
在上单调递增,
,
即,f(x)与g(x)具有“H类关系”.
成功不必自我,功力必不唐捐! 第 6 页 共 6 页
同课章节目录
