人教版高中数学必修二《3.1直线的斜率与倾斜角》优质全国赛课课件(共37张PPT)
文档属性
| 名称 | 人教版高中数学必修二《3.1直线的斜率与倾斜角》优质全国赛课课件(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-25 16:51:41 | ||
图片预览









文档简介
(共37张PPT)
3.1
直线的倾斜角与斜率
【学习目标】
1、正确理解直线的倾斜角和斜率的概念。
2、斜率公式的推导过程,掌握过两点的直线的斜率公式。
3、体会数形结合,分类讨论,
特殊到一般等数学思想,
4、培养勇于探索和团队协作精神。
【核心素养】
数学建模、逻辑推理、数学运算、数据处理。
一、情境引入
西游记---魅力金箍棒
一、情境引入
一、情境引入
一、情境引入
一、情境引入
一、情境引入
一、情境引入
l
P
一、情境引入
l
P
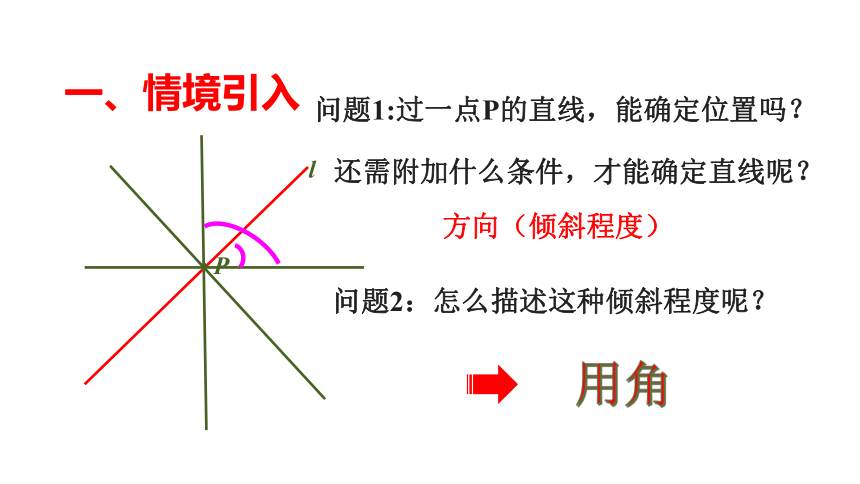
问题1:过一点P的直线,能确定位置吗?
一、情境引入
方向(倾斜程度)
问题2:怎么描述这种倾斜程度呢?
用角
还需附加什么条件,才能确定直线呢?
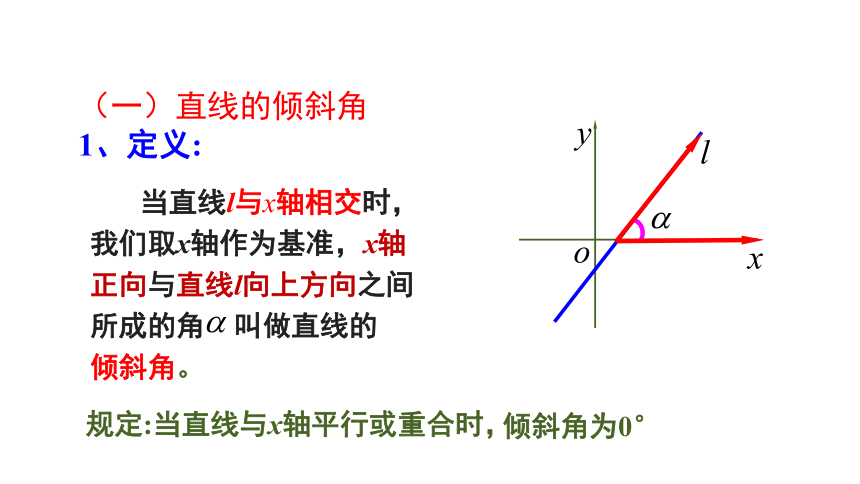
(一)直线的倾斜角
1、定义:
当直线l与x轴相交时,
我们取x轴作为基准,x轴
正向与直线l向上方向之间
所成的角
叫做直线的
倾斜角。
规定:当直线与x轴平行或重合时,
倾斜角为0°
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
按倾斜角分类,直线可分几类?
范围:
0°角
锐角
直角
钝角
日常生活中,还有没有表示倾斜程度的量?
前进量
升
高
量
问题
倾斜角
的正切值
前进量
升
高
量
升高量
前进量
A
B
C
二、直线的斜率:
定义:
我们把一条直线的倾斜角
的正切值叫做这条直线的斜率.
用小写字母
k
表示,即:
练习:
2.倾斜角为锐角时,斜率的大小怎样变化?
1.斜率正负是怎样变化的?
思考:随着倾斜角大小变化,斜率如何变化?
3.倾斜角为钝角时,斜率的大小怎样变化?
y
o
x
模拟演示
几何画板
模拟演示
特殊
一般
a
tan
=
k
倾斜角增大,斜率增大
倾斜角增大,斜率增大
斜率与倾斜角的关系
k
a
O
例
右图中的直线l1、l2、l3的斜率分别为
k1、k2、k3,则(
).
A
.k1<k2<k3
B.
k3<k1<k2
C.
k3<k2<k1
D.
k1<k3<k2
?
D
想一想
已知直线上的两点P1(X1,Y1)
,
P2(X2,Y2),怎样求直线的斜率呢?
探
究:
合作探究
小组讨论
3分钟
推选代表
展示成果
5分钟
学生活动
学生活动---我当小老师
独立思考
自主推导
2分钟
三、由两点确定的直线的斜率:
探
究:
探究一:
已知两点坐标求直线的斜率
问题一:倾斜角为锐角,斜率公式?(1-3组)
问题二:倾斜角为钝角,斜率公式?(4-6组)
问题三:斜率公式与两点的顺序有关吗?
问题四:倾斜角为直角,斜率公式使用吗?
问题五:倾斜角为0度,斜率公式适用吗?
探究二:
已知两点坐标求直线的斜率
探
究:
能不能构造一个直角三角形去求?
三、由两点确定的直线的斜率:
当α为锐角时,
探
究:
当α为钝角时,
倾斜角是钝角时
探
究:
x
y
o
(3)
y
o
x
(4)
探究3:当
的位置对调时,
值又如何呢?
上述公式计算直线
AB
斜率时与两点坐标的顺序无关
讨论:
探究4:.当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?
答:成立,因为分子为0,分母不为0,
k
=0
讨论:
探究5:当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
答:斜率不存在,
因为分母为0。
讨论:
x
y
o
形
数
三、直线的斜率公式:
综上所述,我们得到经过两点
的直线的斜率公式:
结论:
1、当直线与
x
轴平行或重合时,斜率为0,公式适用;
2、当直线与
x
轴垂直时,斜率不存在,公式不适用。
数形结合
例1:如图,已知A(4,2)、B(-8,2)、C(0,-2),求直线AB、BC、CA的斜率,并判断这些直线的倾斜角是什么角?
y
x
o
.
.
.
.
.
.
.
.
.
.
A
B
C
∴直线CA的倾斜角为锐角
∴直线BC的倾斜角为钝角
解:
∴直线AB的倾斜角为零
四、典型例题
四、典型例题
y
x
o
.
.
.
.
.
.
.
.
.
B
A
P
.
.
例3:
解:
数学
运算
知识树
知识层面
一般到
特殊
数学思想
倾斜角与斜率
倾斜角
数形结合
斜率
斜率的计算公式
分类
讨论
课
堂
小
结
数据
推理
核心素养
数据
分析
数学
抽象
1、必做题:习题2.2
(A组)7、8题;
2、选做题:(B组)2题.3(1).
六.作业布置
六.数学文化
笔直似光芒,
延伸无限长。
一点加方向,
确定没商量。
谢谢大家!
3.1
直线的倾斜角与斜率
【学习目标】
1、正确理解直线的倾斜角和斜率的概念。
2、斜率公式的推导过程,掌握过两点的直线的斜率公式。
3、体会数形结合,分类讨论,
特殊到一般等数学思想,
4、培养勇于探索和团队协作精神。
【核心素养】
数学建模、逻辑推理、数学运算、数据处理。
一、情境引入
西游记---魅力金箍棒
一、情境引入
一、情境引入
一、情境引入
一、情境引入
一、情境引入
一、情境引入
l
P
一、情境引入
l
P
问题1:过一点P的直线,能确定位置吗?
一、情境引入
方向(倾斜程度)
问题2:怎么描述这种倾斜程度呢?
用角
还需附加什么条件,才能确定直线呢?
(一)直线的倾斜角
1、定义:
当直线l与x轴相交时,
我们取x轴作为基准,x轴
正向与直线l向上方向之间
所成的角
叫做直线的
倾斜角。
规定:当直线与x轴平行或重合时,
倾斜角为0°
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
按倾斜角分类,直线可分几类?
范围:
0°角
锐角
直角
钝角
日常生活中,还有没有表示倾斜程度的量?
前进量
升
高
量
问题
倾斜角
的正切值
前进量
升
高
量
升高量
前进量
A
B
C
二、直线的斜率:
定义:
我们把一条直线的倾斜角
的正切值叫做这条直线的斜率.
用小写字母
k
表示,即:
练习:
2.倾斜角为锐角时,斜率的大小怎样变化?
1.斜率正负是怎样变化的?
思考:随着倾斜角大小变化,斜率如何变化?
3.倾斜角为钝角时,斜率的大小怎样变化?
y
o
x
模拟演示
几何画板
模拟演示
特殊
一般
a
tan
=
k
倾斜角增大,斜率增大
倾斜角增大,斜率增大
斜率与倾斜角的关系
k
a
O
例
右图中的直线l1、l2、l3的斜率分别为
k1、k2、k3,则(
).
A
.k1<k2<k3
B.
k3<k1<k2
C.
k3<k2<k1
D.
k1<k3<k2
?
D
想一想
已知直线上的两点P1(X1,Y1)
,
P2(X2,Y2),怎样求直线的斜率呢?
探
究:
合作探究
小组讨论
3分钟
推选代表
展示成果
5分钟
学生活动
学生活动---我当小老师
独立思考
自主推导
2分钟
三、由两点确定的直线的斜率:
探
究:
探究一:
已知两点坐标求直线的斜率
问题一:倾斜角为锐角,斜率公式?(1-3组)
问题二:倾斜角为钝角,斜率公式?(4-6组)
问题三:斜率公式与两点的顺序有关吗?
问题四:倾斜角为直角,斜率公式使用吗?
问题五:倾斜角为0度,斜率公式适用吗?
探究二:
已知两点坐标求直线的斜率
探
究:
能不能构造一个直角三角形去求?
三、由两点确定的直线的斜率:
当α为锐角时,
探
究:
当α为钝角时,
倾斜角是钝角时
探
究:
x
y
o
(3)
y
o
x
(4)
探究3:当
的位置对调时,
值又如何呢?
上述公式计算直线
AB
斜率时与两点坐标的顺序无关
讨论:
探究4:.当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?
答:成立,因为分子为0,分母不为0,
k
=0
讨论:
探究5:当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
答:斜率不存在,
因为分母为0。
讨论:
x
y
o
形
数
三、直线的斜率公式:
综上所述,我们得到经过两点
的直线的斜率公式:
结论:
1、当直线与
x
轴平行或重合时,斜率为0,公式适用;
2、当直线与
x
轴垂直时,斜率不存在,公式不适用。
数形结合
例1:如图,已知A(4,2)、B(-8,2)、C(0,-2),求直线AB、BC、CA的斜率,并判断这些直线的倾斜角是什么角?
y
x
o
.
.
.
.
.
.
.
.
.
.
A
B
C
∴直线CA的倾斜角为锐角
∴直线BC的倾斜角为钝角
解:
∴直线AB的倾斜角为零
四、典型例题
四、典型例题
y
x
o
.
.
.
.
.
.
.
.
.
B
A
P
.
.
例3:
解:
数学
运算
知识树
知识层面
一般到
特殊
数学思想
倾斜角与斜率
倾斜角
数形结合
斜率
斜率的计算公式
分类
讨论
课
堂
小
结
数据
推理
核心素养
数据
分析
数学
抽象
1、必做题:习题2.2
(A组)7、8题;
2、选做题:(B组)2题.3(1).
六.作业布置
六.数学文化
笔直似光芒,
延伸无限长。
一点加方向,
确定没商量。
谢谢大家!
