19.2正方形
图片预览


文档简介
(共27张PPT)
我们学过哪些特殊四 边形?
一.特殊四边形的性质分别是:
平行四边形的性质是:
矩形的性质是:
菱形的性质是:
1.直角三角形中, 30度角所对的________
2.直角三角形中, 如果直角边是斜边的一半,
它所对的角是________
3.直角三角形中,斜边上的_____________
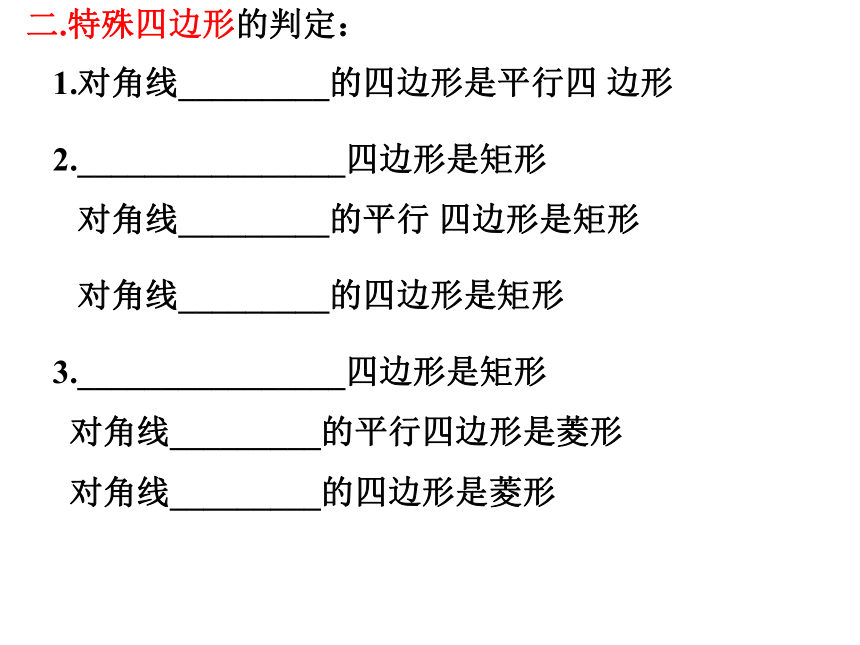
1.对角线_________的四边形是平行四 边形
2.________________四边形是矩形
对角线_________的平行 四边形是矩形
对角线_________的四边形是矩形
3.________________四边形是矩形
对角线_________的平行四边形是菱形
对角线_________的四边形是菱形
二.特殊四边形的判定:
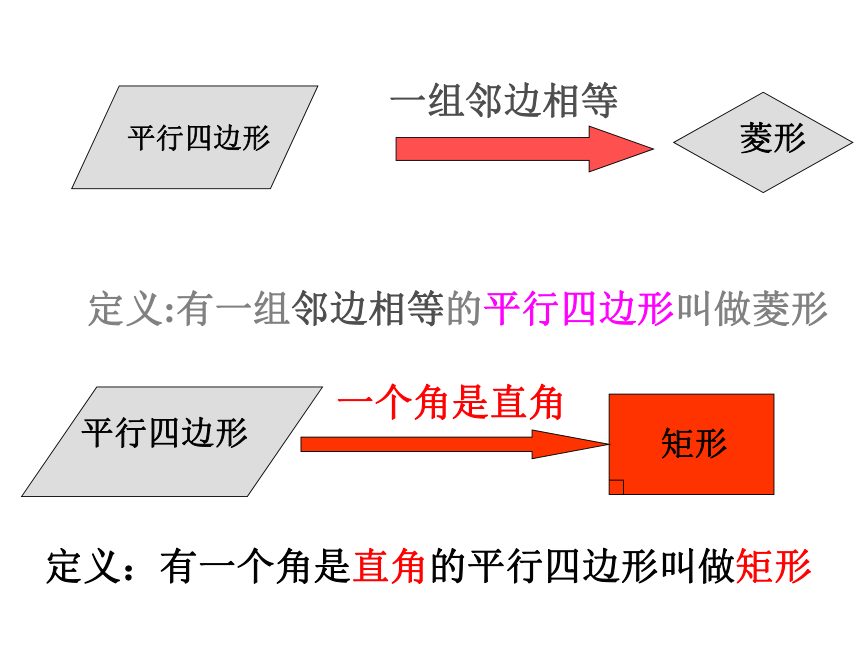
平行四边形
菱形
定义:有一组邻边相等的平行四边形叫做菱形
平行四边形
一个角是直角
矩形
定义:有一个角是直角的平行四边形叫做矩形
一组邻边相等
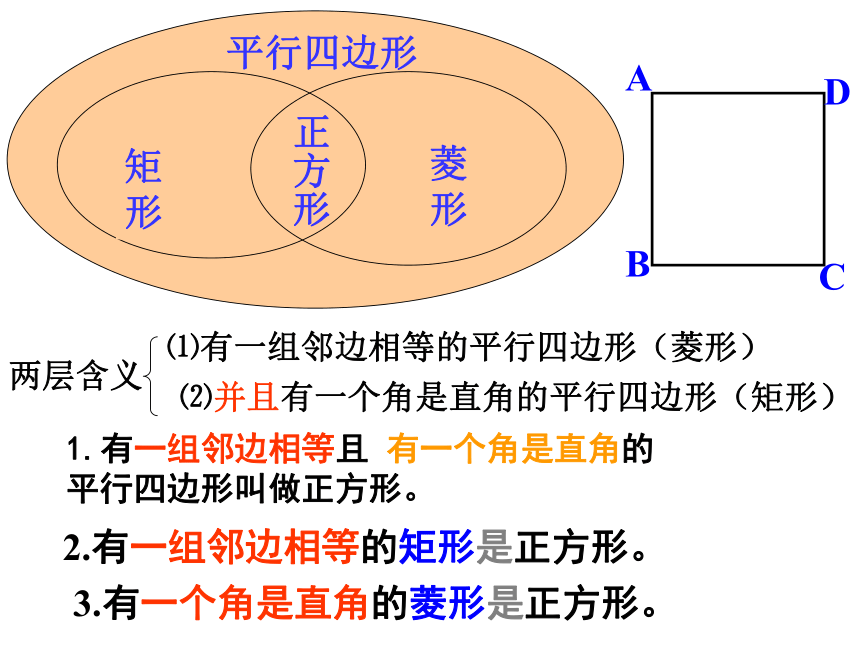
平行四边形
矩形
菱形
正方形
⑴有一组邻边相等的平行四边形(菱形)
⑵并且有一个角是直角的平行四边形(矩形)
两层含义
2.有一组邻边相等的矩形是正方形。
1.有一组邻边相等且 有一个角是直角的
平行四边形叫做正方形。
3.有一个角是直角的菱形是正方形。
A
B
C
D
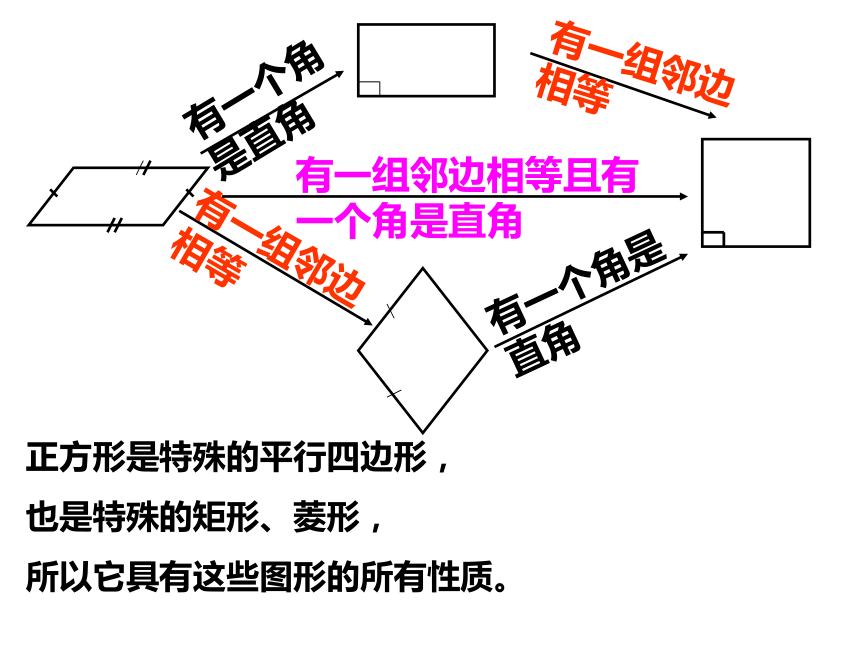
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
正方形是特殊的平行四边形,
也是特殊的矩形、菱形,
所以它具有这些图形的所有性质。
2.图中有哪些角,哪些边相等?
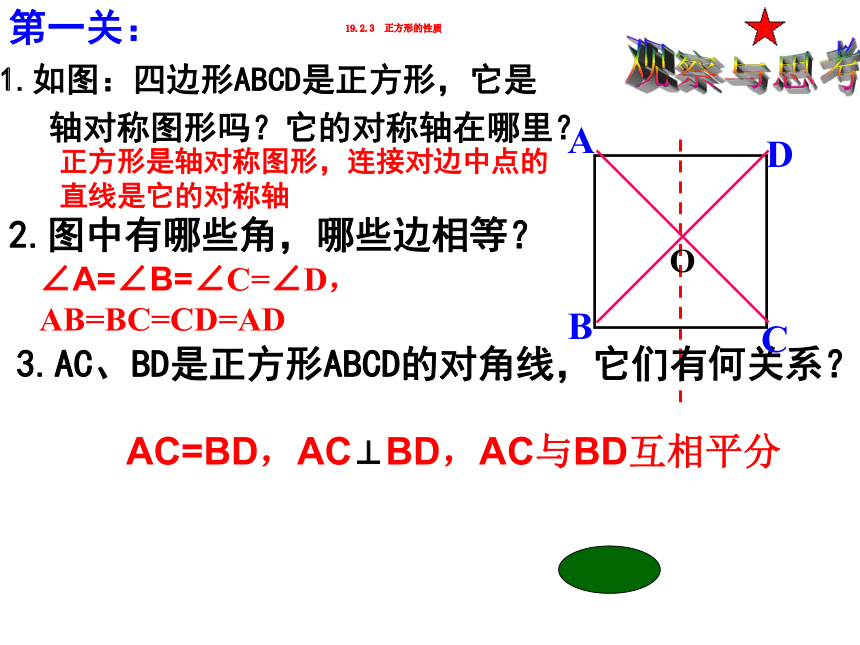
1.如图:四边形ABCD是正方形,它是
轴对称图形吗?它的对称轴在哪里?
正方形是轴对称图形,连接对边中点的直线是它的对称轴
∠A=∠B=∠C=∠D,AB=BC=CD=AD
第一关:
3.AC、BD是正方形ABCD的对角线,它们有何关系?
AC=BD,AC⊥BD,AC与BD互相平分
A
B
C
D
O
对称轴
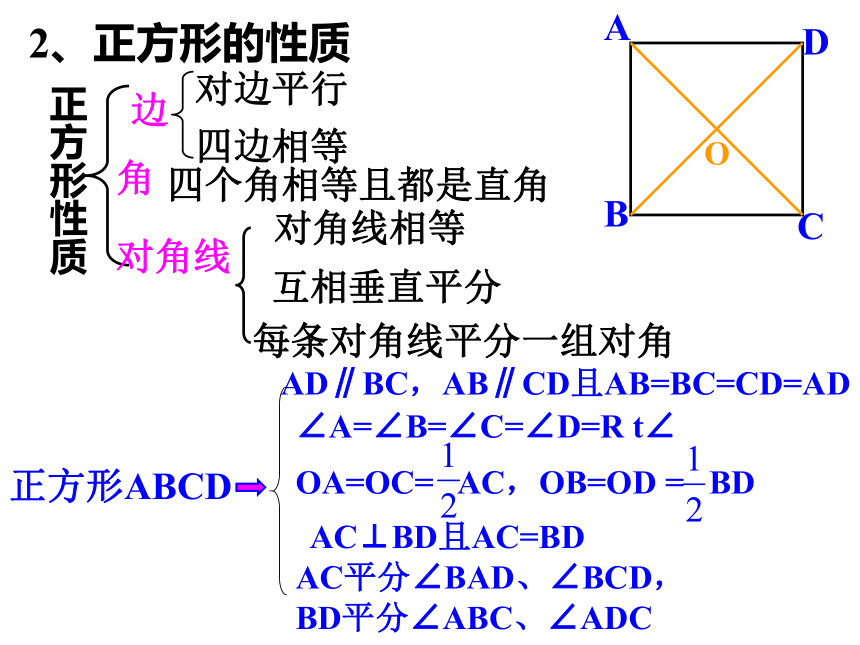
2、正方形的性质
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角
正方形性质
A
B
C
D
正方形ABCD
AD∥BC,AB∥CD且AB=BC=CD=AD
∠A=∠B=∠C=∠D=R t∠
OA=OC= AC,OB=OD = BD
AC⊥BD且AC=BD
AC平分∠BAD、∠BCD,
BD平分∠ABC、∠ADC
O
A
B
C
D
O
怎样判定一个四边形是正方形呢?
1.有一组邻边相等且 有一个角是直角的平行四边形叫做正方形。
2.有一组邻边相等的矩形是正方形。
3.有一个角是直角的菱形是正方形。
先判定四边形是矩形,再判定这个矩形又是菱形;
先判定四边形是菱形,再判定这个菱形也是矩形。
例1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
A
B
C
D
O
图中有多少个等腰三角形?
△ABO,△BCO,△CDO, △DAO;
△ABD,△BCD,△ABC,△ADC。
△ABO≌△BCO≌△CDO≌△DAO;
△ABD≌△BCD≌△ABC≌△ADC。
第二关:
已知:如图,正方形ABCD的对角线
AC与BD交于点O。
求证: △ABO.△BCO.△CDO.△DAO都是等腰直角三
角形,且△ABO≌△BCO≌△CDO≌△DAO.
判断题:
(1)正方形既是平行四边形,又是矩形,又是菱形.( )
(2)正方形的两条对角线相等,且互相垂直. ( )
(3)正方形的每一条对角线平分一组对角. ( )
(4)一组邻边相等,且两条对角线相等的平行
四边形是正方形. ( )
(5)两条对角线相等,且互相垂直的四边形是
正方形. ( )
√
√
√
√
×
1.如图:△ABC中,∠ACB=90°,
CD是角平分线,DE⊥AC,DF⊥BC,
垂足分别为E、F。求证:DECF是正方形
E
A
C
B
D
F
2. 如图:分别以△ABC的边AB、AC为边向外
画正方形AEDB和正方形ACFG,连结CE、BG,
求证:BG=CE
A
B
C
F
G
D
E
第三关:
3.如图:正方形ABCD中,∠DAF=25°,
AF交对角线BD于E,交CD于F,
则∠BEC= 度
A
B
C
D
E
4.如图:E是正方形ABCD内一点,且EC=AB=BE
则∠DEC= 度
A
B
C
F
D
E
第四关:
例2:四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数。
8
解:∵四边形ABCD是正方形
∴AC⊥BD ∠AOB=900
∠BAC=∠DAC
∴∠OAB=450
A
B
C
D
O
E
F
(2)若AC=4,则正方形边长为 ; 正方形的面积是
4㎝
(3)正方形的面积64cm2,则对角线交点到正方形一边的距离
2√2
例3.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
你能完成证明吗
AB=BC,∠1=∠2=45 ° 条件够吗?
还需要的条件是 AM=BN
△ABM≌△BCN △CBM≌△DCN
你所要证明的两个三角形已经满足
了哪些条件
由正方形可以得到的条件有:
例3.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN
下面大家自己完成证明
教学小结:
一.
二.正方形的判定:
1. 有一组邻边相等且 有一个角是
直角的平行四边形叫做正方形。
2.有一组邻边相等的矩形是正方形。
3.有一个角是直角的菱形是正方形。
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角
正方形性质
我们学过哪些特殊四 边形?
平行四边形
两组对边分别平行
四边形
一个角是直角
一组邻边相等
一组邻边相等
一个角是直角
一.特殊四边形的性质分别是:
平行四边形的性质是:
1.直角三角形中, 30度角所对的________
2.直角三角形中, 如果直角边是斜边的一半,
它所对的角是________
3.直角三角形中,斜边上的_____________
例4.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
试一试
看能不能完成证明
△CMD≌△ADF
例4.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°
证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
范例精讲 例5:已知:如图(2),点A‘、B’、C‘、D’分别是正方形ABCD 的边AB、BC、CD、DA的中点,
求证:四边形A'B'C'D'是正方形。
分析(1)你能证明四边形是矩形吗?
(2)你能证明四边形是菱形吗?
(3)你能证明四边形是正方形吗?
请大家完成证明
O
练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2)。
求:AC的长及正方形的面积S。
练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6cm,如图
求:正方形的面积S。
例6.已知:如图(4)矩形ABCD中,∠A、∠B、∠C、∠D 的平分线组成四边形A'B'C'D',
分析:
判定一个四边形是正方形可以选择:
求证:四边形A'B'C'D'是正方形。
下面请大家进行证明。
(1)先证明它是矩形,再证它有一组邻 边相等;
(2)先证明它是菱形,再证它有一个角等于90°
已知:如图(4)矩形ABCD中,∠A、∠B、∠C、∠D的 平分线组成四边形A'B'C'D',
证明:在四边形ABCD中
求证:四边形A'B'C'D'是正方形。
又∵AB‘=BD’ 且AA‘=BA’(已证) AB'-AA'=BD'-BA' A'B'=A'D' ∴四边形A'B'C'D'是正方形(有一组邻边相等的矩形是正方形)
∵AB'、BD'、CD'、DB'分别平分∠DAB、∠ABC、∠BCD、∠CDA
∴∠B'=∠D'=90°
∴∠1=∠2=∠3=∠4=45°
AD=BC ∴△AB'D≌△BD'C (ASA) ∴AB'=BD'=CD'=DB' 同理可证:∠D'A'B'=∠D'C'B'=90且AA'=BA'=CC'=DC' ∴四边形A'B'C'D'是矩形(有三个角都是直角的四边形是矩形)
我们学过哪些特殊四 边形?
一.特殊四边形的性质分别是:
平行四边形的性质是:
矩形的性质是:
菱形的性质是:
1.直角三角形中, 30度角所对的________
2.直角三角形中, 如果直角边是斜边的一半,
它所对的角是________
3.直角三角形中,斜边上的_____________
1.对角线_________的四边形是平行四 边形
2.________________四边形是矩形
对角线_________的平行 四边形是矩形
对角线_________的四边形是矩形
3.________________四边形是矩形
对角线_________的平行四边形是菱形
对角线_________的四边形是菱形
二.特殊四边形的判定:
平行四边形
菱形
定义:有一组邻边相等的平行四边形叫做菱形
平行四边形
一个角是直角
矩形
定义:有一个角是直角的平行四边形叫做矩形
一组邻边相等
平行四边形
矩形
菱形
正方形
⑴有一组邻边相等的平行四边形(菱形)
⑵并且有一个角是直角的平行四边形(矩形)
两层含义
2.有一组邻边相等的矩形是正方形。
1.有一组邻边相等且 有一个角是直角的
平行四边形叫做正方形。
3.有一个角是直角的菱形是正方形。
A
B
C
D
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
正方形是特殊的平行四边形,
也是特殊的矩形、菱形,
所以它具有这些图形的所有性质。
2.图中有哪些角,哪些边相等?
1.如图:四边形ABCD是正方形,它是
轴对称图形吗?它的对称轴在哪里?
正方形是轴对称图形,连接对边中点的直线是它的对称轴
∠A=∠B=∠C=∠D,AB=BC=CD=AD
第一关:
3.AC、BD是正方形ABCD的对角线,它们有何关系?
AC=BD,AC⊥BD,AC与BD互相平分
A
B
C
D
O
对称轴
2、正方形的性质
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角
正方形性质
A
B
C
D
正方形ABCD
AD∥BC,AB∥CD且AB=BC=CD=AD
∠A=∠B=∠C=∠D=R t∠
OA=OC= AC,OB=OD = BD
AC⊥BD且AC=BD
AC平分∠BAD、∠BCD,
BD平分∠ABC、∠ADC
O
A
B
C
D
O
怎样判定一个四边形是正方形呢?
1.有一组邻边相等且 有一个角是直角的平行四边形叫做正方形。
2.有一组邻边相等的矩形是正方形。
3.有一个角是直角的菱形是正方形。
先判定四边形是矩形,再判定这个矩形又是菱形;
先判定四边形是菱形,再判定这个菱形也是矩形。
例1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
A
B
C
D
O
图中有多少个等腰三角形?
△ABO,△BCO,△CDO, △DAO;
△ABD,△BCD,△ABC,△ADC。
△ABO≌△BCO≌△CDO≌△DAO;
△ABD≌△BCD≌△ABC≌△ADC。
第二关:
已知:如图,正方形ABCD的对角线
AC与BD交于点O。
求证: △ABO.△BCO.△CDO.△DAO都是等腰直角三
角形,且△ABO≌△BCO≌△CDO≌△DAO.
判断题:
(1)正方形既是平行四边形,又是矩形,又是菱形.( )
(2)正方形的两条对角线相等,且互相垂直. ( )
(3)正方形的每一条对角线平分一组对角. ( )
(4)一组邻边相等,且两条对角线相等的平行
四边形是正方形. ( )
(5)两条对角线相等,且互相垂直的四边形是
正方形. ( )
√
√
√
√
×
1.如图:△ABC中,∠ACB=90°,
CD是角平分线,DE⊥AC,DF⊥BC,
垂足分别为E、F。求证:DECF是正方形
E
A
C
B
D
F
2. 如图:分别以△ABC的边AB、AC为边向外
画正方形AEDB和正方形ACFG,连结CE、BG,
求证:BG=CE
A
B
C
F
G
D
E
第三关:
3.如图:正方形ABCD中,∠DAF=25°,
AF交对角线BD于E,交CD于F,
则∠BEC= 度
A
B
C
D
E
4.如图:E是正方形ABCD内一点,且EC=AB=BE
则∠DEC= 度
A
B
C
F
D
E
第四关:
例2:四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数。
8
解:∵四边形ABCD是正方形
∴AC⊥BD ∠AOB=900
∠BAC=∠DAC
∴∠OAB=450
A
B
C
D
O
E
F
(2)若AC=4,则正方形边长为 ; 正方形的面积是
4㎝
(3)正方形的面积64cm2,则对角线交点到正方形一边的距离
2√2
例3.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
你能完成证明吗
AB=BC,∠1=∠2=45 ° 条件够吗?
还需要的条件是 AM=BN
△ABM≌△BCN △CBM≌△DCN
你所要证明的两个三角形已经满足
了哪些条件
由正方形可以得到的条件有:
例3.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN
下面大家自己完成证明
教学小结:
一.
二.正方形的判定:
1. 有一组邻边相等且 有一个角是
直角的平行四边形叫做正方形。
2.有一组邻边相等的矩形是正方形。
3.有一个角是直角的菱形是正方形。
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角
正方形性质
我们学过哪些特殊四 边形?
平行四边形
两组对边分别平行
四边形
一个角是直角
一组邻边相等
一组邻边相等
一个角是直角
一.特殊四边形的性质分别是:
平行四边形的性质是:
1.直角三角形中, 30度角所对的________
2.直角三角形中, 如果直角边是斜边的一半,
它所对的角是________
3.直角三角形中,斜边上的_____________
例4.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
试一试
看能不能完成证明
△CMD≌△ADF
例4.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°
证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
范例精讲 例5:已知:如图(2),点A‘、B’、C‘、D’分别是正方形ABCD 的边AB、BC、CD、DA的中点,
求证:四边形A'B'C'D'是正方形。
分析(1)你能证明四边形是矩形吗?
(2)你能证明四边形是菱形吗?
(3)你能证明四边形是正方形吗?
请大家完成证明
O
练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2)。
求:AC的长及正方形的面积S。
练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6cm,如图
求:正方形的面积S。
例6.已知:如图(4)矩形ABCD中,∠A、∠B、∠C、∠D 的平分线组成四边形A'B'C'D',
分析:
判定一个四边形是正方形可以选择:
求证:四边形A'B'C'D'是正方形。
下面请大家进行证明。
(1)先证明它是矩形,再证它有一组邻 边相等;
(2)先证明它是菱形,再证它有一个角等于90°
已知:如图(4)矩形ABCD中,∠A、∠B、∠C、∠D的 平分线组成四边形A'B'C'D',
证明:在四边形ABCD中
求证:四边形A'B'C'D'是正方形。
又∵AB‘=BD’ 且AA‘=BA’(已证) AB'-AA'=BD'-BA' A'B'=A'D' ∴四边形A'B'C'D'是正方形(有一组邻边相等的矩形是正方形)
∵AB'、BD'、CD'、DB'分别平分∠DAB、∠ABC、∠BCD、∠CDA
∴∠B'=∠D'=90°
∴∠1=∠2=∠3=∠4=45°
AD=BC ∴△AB'D≌△BD'C (ASA) ∴AB'=BD'=CD'=DB' 同理可证:∠D'A'B'=∠D'C'B'=90且AA'=BA'=CC'=DC' ∴四边形A'B'C'D'是矩形(有三个角都是直角的四边形是矩形)
