一次函数单元测试题(无答案)
图片预览

文档简介
一次函数单元测试题
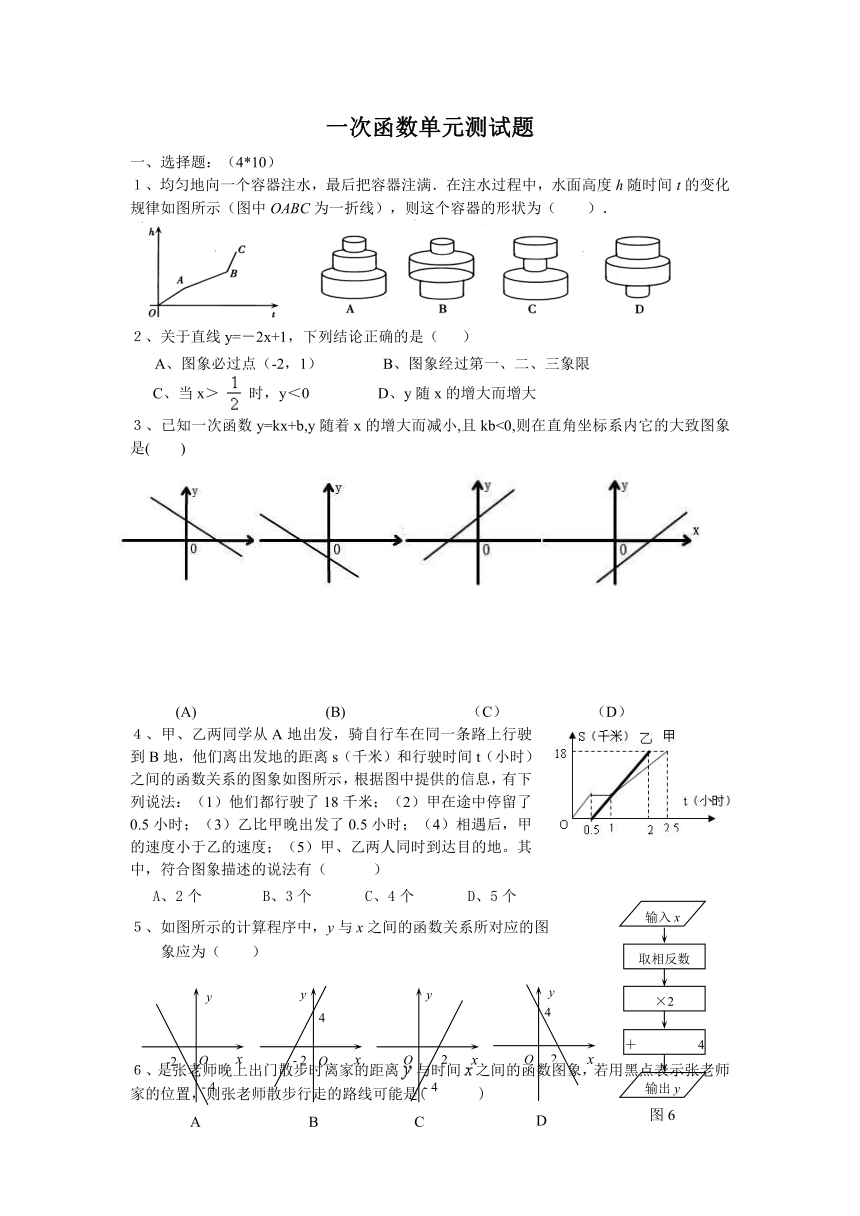
一、选择题:(4*10)
1、均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化
规律如图所示(图中OABC为一折线),则这个容器的形状为( ).
2、关于直线y=-2x+1,下列结论正确的是( )
A、图象必过点(-2,1) B、图象经过第一、二、三象限
C、当x> 时,y<0 D、y随x的增大而增大
3、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)
4、甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,根据图中提供的信息,有下列说法:(1)他们都行驶了18千米;(2)甲在途中停留了0.5小时;(3)乙比甲晚出发了0.5小时;(4)相遇后,甲的速度小于乙的速度;(5)甲、乙两人同时到达目的地。其中,符合图象描述的说法有( )
A、2个 B、3个 C、4个 D、5个
5、如图所示的计算程序中,y与x之间的函数关系所对应的图
象应为( )
6、是张老师晚上出门散步时离家的距离与时间之间的函数图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
7.小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与卖瓜的千克数之间的关系如图所示,那么小李赚了( )
A.32元 B.36元 C.38元 D.44元、
8.下列函数中,y随x的增大而减小的有( )
① ② ③ ④
A.1个 B.2个 C.3个 D.4个
9.直线 y=x+4与 x轴交于 A,与y轴交于B, O为原点,则△AOB的面积为( )
A.12 B.24 C.6 D.10
10.一天,小军和爸爸去登山,已知山脚到山顶的路程为300米.小军先走了一段路程,爸爸才开始出发.图中两条线段分别表示小军和爸爸离开山脚登山的路程S(米)与登山所用的时间t(分)的关系(从爸爸开始登山时计时).根据图象,下列说法错误的是( )
A.爸爸登山时,小军已走了50米
B.爸爸走了5分钟,小军仍在爸爸的前面
C.小军比爸爸晚到山顶
D.爸爸前10分钟登山的速度比小军慢,10分钟后登山的速度比小军快
二、填空题 (4*10)
1、已知点P(-3,5),则点P关于x轴对称的点P1的坐标是_____点P关于y轴对称的点P2的的坐标是_____,点P关于原点对称的点P3的坐标是_____。8、点P在第二象限内,若P到x轴的距离是3,到y轴的距离是4,那么点P的坐标为
2、若点M(m,m-3)在第四象限,则m的取值范围是________。写一个经过一、二、三象限的一次函数 将直线y=3x向下平移5个单位,得到直线 ;
3、已知一个正比例函数的图象经过点(-2,4),则这个正比例函数的表达式是
4、已知y是x的一次函数,下表中列出了部分对应值,则m=_。
x -1 0 1
y 1 m -1
5. 一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的解析式可以
是 .(任写出一个符合题意即可)
6. 汽车工作时油箱中的燃油量y(升)与汽车工作时间t(小时)之间的函数图象如下中图所
示,汽车开始工作时油箱中有燃油 升,经过 小时耗尽燃油,y与x之间的
函数关系式为 .7. 如图所示的折线ABC为某地出租汽车收费y(元)与乘坐路程x(千米)之间的函数关系式图
象,当x≥3千米时,该函数的解析式为 ,乘坐2千米时,车费为 元,
乘坐8千米时,车费为 元.
. (第6题) (第7题) 8.如图,直线经过,两点,则不等式的解集为 .
9.如图,已知函数和的图象交点为,则不等式的解集为 .
(第8题图)
10.如下图所示,利用函数图象回答下列问题:
(1)方程组 的解为__________; (2)不等式2x>-x+3的解集为___________;
(3)不等式2x<-x+3的解集为__________.
三、解答题:(10+10+10+15+15)
21、已知与成正比例,且时,.
(1)求与的函数关系式;
(2)当= 时,求的值;
(3)将所得函数图象平移,使它过点(2, -1).求平移后直线的解析式.
22、如右图,在直角坐标系中,直线y=kx+4与x 轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式。
23、已知,直线y=2x+3与直线y=-2x-1.
求两直线与y轴交点A,B的坐标;
求两直线交点C的坐标; ( http: / / www.1230.org )
求△ABC的面积.
24、我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元水费,超过的部分每吨按b元(b>a)收费.设一户居民月用水y元,y与x之间的函数关系如图所示.
求a的值,若某户居民上月用水8吨,应收水费多少元
求b的值,并写出当x大于10时,y与x之间的函数关系;
已知居民甲上月比居民乙多用水4吨,两家共收水费46
元,求他们上月分别用水多少吨
25.某化妆公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.
设(件)是销售商品的数量,(元)是销售人员的月工资.
如右图所示,为方案一的函数图象,为方案二的函数图象.
已知每件商品的销售提成方案二比方案一少7元.从图中信息解
答如下问题(注:销售提成是指从销售每件商品得到的销售费中
提取一定数量的费用):
(1)求的函数解析式;
(2)请问方案二中每月付给销售人员的底薪是多少元?(3)如果该公司销售人员小丽的月工资要超过1000元,那么小丽选用哪种方案最好,至少要销售商品多少件?
取相反数
×2
+4
图6
输入x
输出y
O
y
x
-2
- 4
A
D
C
B
O
4
2
y
O
2
- 4
y
x
O
4
- 2
y
x
x
(第10题)
O
(第9题图)
x
y
1
P
y=x+b
y=ax+3
y
x
O
A
B
x
y
A
B
C
420
560
30
O
x(件)
y(元)
一、选择题:(4*10)
1、均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化
规律如图所示(图中OABC为一折线),则这个容器的形状为( ).
2、关于直线y=-2x+1,下列结论正确的是( )
A、图象必过点(-2,1) B、图象经过第一、二、三象限
C、当x> 时,y<0 D、y随x的增大而增大
3、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)
4、甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,根据图中提供的信息,有下列说法:(1)他们都行驶了18千米;(2)甲在途中停留了0.5小时;(3)乙比甲晚出发了0.5小时;(4)相遇后,甲的速度小于乙的速度;(5)甲、乙两人同时到达目的地。其中,符合图象描述的说法有( )
A、2个 B、3个 C、4个 D、5个
5、如图所示的计算程序中,y与x之间的函数关系所对应的图
象应为( )
6、是张老师晚上出门散步时离家的距离与时间之间的函数图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
7.小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与卖瓜的千克数之间的关系如图所示,那么小李赚了( )
A.32元 B.36元 C.38元 D.44元、
8.下列函数中,y随x的增大而减小的有( )
① ② ③ ④
A.1个 B.2个 C.3个 D.4个
9.直线 y=x+4与 x轴交于 A,与y轴交于B, O为原点,则△AOB的面积为( )
A.12 B.24 C.6 D.10
10.一天,小军和爸爸去登山,已知山脚到山顶的路程为300米.小军先走了一段路程,爸爸才开始出发.图中两条线段分别表示小军和爸爸离开山脚登山的路程S(米)与登山所用的时间t(分)的关系(从爸爸开始登山时计时).根据图象,下列说法错误的是( )
A.爸爸登山时,小军已走了50米
B.爸爸走了5分钟,小军仍在爸爸的前面
C.小军比爸爸晚到山顶
D.爸爸前10分钟登山的速度比小军慢,10分钟后登山的速度比小军快
二、填空题 (4*10)
1、已知点P(-3,5),则点P关于x轴对称的点P1的坐标是_____点P关于y轴对称的点P2的的坐标是_____,点P关于原点对称的点P3的坐标是_____。8、点P在第二象限内,若P到x轴的距离是3,到y轴的距离是4,那么点P的坐标为
2、若点M(m,m-3)在第四象限,则m的取值范围是________。写一个经过一、二、三象限的一次函数 将直线y=3x向下平移5个单位,得到直线 ;
3、已知一个正比例函数的图象经过点(-2,4),则这个正比例函数的表达式是
4、已知y是x的一次函数,下表中列出了部分对应值,则m=_。
x -1 0 1
y 1 m -1
5. 一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的解析式可以
是 .(任写出一个符合题意即可)
6. 汽车工作时油箱中的燃油量y(升)与汽车工作时间t(小时)之间的函数图象如下中图所
示,汽车开始工作时油箱中有燃油 升,经过 小时耗尽燃油,y与x之间的
函数关系式为 .7. 如图所示的折线ABC为某地出租汽车收费y(元)与乘坐路程x(千米)之间的函数关系式图
象,当x≥3千米时,该函数的解析式为 ,乘坐2千米时,车费为 元,
乘坐8千米时,车费为 元.
. (第6题) (第7题) 8.如图,直线经过,两点,则不等式的解集为 .
9.如图,已知函数和的图象交点为,则不等式的解集为 .
(第8题图)
10.如下图所示,利用函数图象回答下列问题:
(1)方程组 的解为__________; (2)不等式2x>-x+3的解集为___________;
(3)不等式2x<-x+3的解集为__________.
三、解答题:(10+10+10+15+15)
21、已知与成正比例,且时,.
(1)求与的函数关系式;
(2)当= 时,求的值;
(3)将所得函数图象平移,使它过点(2, -1).求平移后直线的解析式.
22、如右图,在直角坐标系中,直线y=kx+4与x 轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式。
23、已知,直线y=2x+3与直线y=-2x-1.
求两直线与y轴交点A,B的坐标;
求两直线交点C的坐标; ( http: / / www.1230.org )
求△ABC的面积.
24、我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元水费,超过的部分每吨按b元(b>a)收费.设一户居民月用水y元,y与x之间的函数关系如图所示.
求a的值,若某户居民上月用水8吨,应收水费多少元
求b的值,并写出当x大于10时,y与x之间的函数关系;
已知居民甲上月比居民乙多用水4吨,两家共收水费46
元,求他们上月分别用水多少吨
25.某化妆公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.
设(件)是销售商品的数量,(元)是销售人员的月工资.
如右图所示,为方案一的函数图象,为方案二的函数图象.
已知每件商品的销售提成方案二比方案一少7元.从图中信息解
答如下问题(注:销售提成是指从销售每件商品得到的销售费中
提取一定数量的费用):
(1)求的函数解析式;
(2)请问方案二中每月付给销售人员的底薪是多少元?(3)如果该公司销售人员小丽的月工资要超过1000元,那么小丽选用哪种方案最好,至少要销售商品多少件?
取相反数
×2
+4
图6
输入x
输出y
O
y
x
-2
- 4
A
D
C
B
O
4
2
y
O
2
- 4
y
x
O
4
- 2
y
x
x
(第10题)
O
(第9题图)
x
y
1
P
y=x+b
y=ax+3
y
x
O
A
B
x
y
A
B
C
420
560
30
O
x(件)
y(元)
