垂直于弦的直径
图片预览







文档简介
(共22张PPT)
24.1.2 垂直于弦的直径
学海中学
教学目标:
1.会利用圆的轴对称性探究垂径定理、证明垂径定理;
2.能利用垂径定理进行相关的计算和证明;
3、掌握垂径定理的推论:圆的两条平行弦所夹的弧相等.
教学重点:
垂径定理的证明与简单应用;
教学难点:
垂径定理的证明定理及其简单应用;
结 论:圆是轴对称图形。
经过圆心的每一条直线都是它的对称轴。
特殊性:对称轴有无数条。
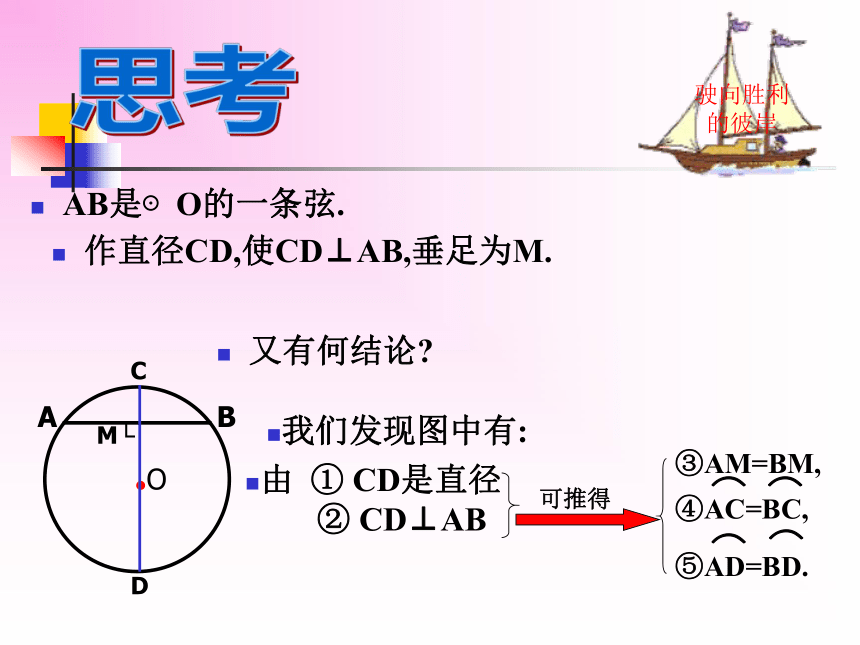
③AM=BM,
AB是⊙O的一条弦.
又有何结论
驶向胜利的彼岸
作直径CD,使CD⊥AB,垂足为M.
●O
我们发现图中有:
A
B
C
D
M└
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理
定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
驶向胜利的彼岸
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
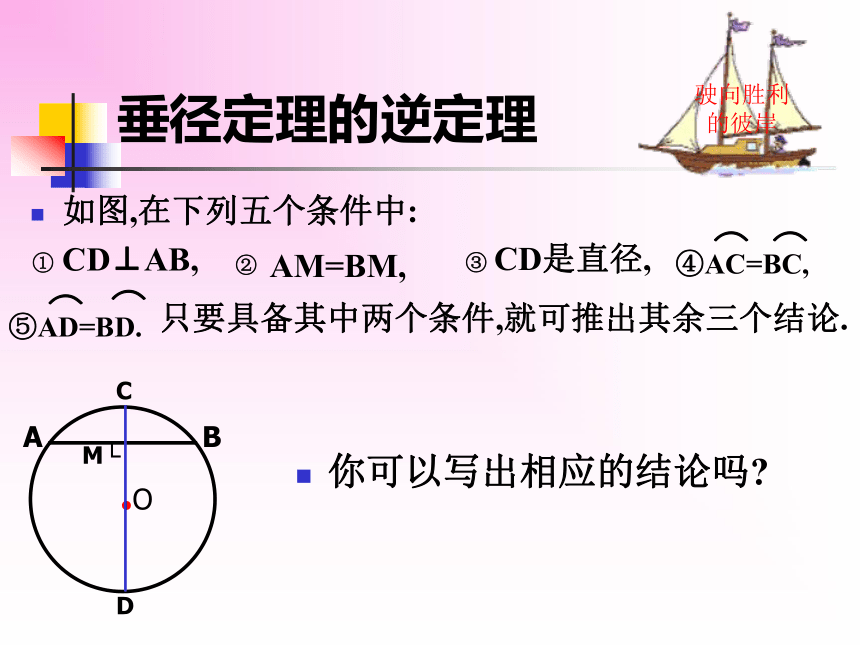
你可以写出相应的结论吗
垂径定理的逆定理
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
驶向胜利的彼岸
●O
A
B
C
D
M└
③ CD是直径,
AM=BM,
① CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
②
垂径定理及其推论.
垂径定理:垂直于弦的直径平分弦,并且平分弦
所对的两条弧.
推论1:平分弦(不是直径)的直径垂直于弦,并且
平分弦所对的两条弧.
推论2:弦的垂直平分线经过圆心,并且平分弦
所对的两条弧.
推论3:平分弦所对的一条弧的直径,垂直平分
弦,并平分弦所对的另一条弧.
驶向胜利的彼岸
挑战自我画一画
如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
试一试P93
12
驶向胜利的彼岸
挑战自我填一填
判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条平行弦所夹的弧相等. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )
B
A
O
应用:
已知如图,在 中,弦AB的长为8cm,若圆心O到AB的距离为3 cm,则 的半径为 cm.
C
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题.
5
例2、如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
求证:AC = BD
A
B
C
D
O
E
证明:过O作OE⊥AB,垂足为E, 则AE = BE, CE = DE
∴AE - CE = BE - DE
即 AC = BD
辅助线:垂直于弦的直径。 实际上从圆心作与弦垂直的线段。
练习
变 换
A
B
C
D
O
1、如图1,在⊙O中, AB是 弦, OC = OD。
求证:AC = BD
(1)
A
B
C
D
O
2、如图2,在⊙O中, CD是
弦, OA = OB。
求证:AC = BD
(2)
2.已知:如图,在⊙O中,AB、AC为互相垂直的两条相等的弦,OD⊥AB,OE⊥AC,D、E为垂足。求证:ADOE为正方形。
O
A
B
C
D
E
练习
1. 在半径为50mm的⊙O中,有长50mm的弦AB。计算:
(1) 点O与AB的距离;
(2)∠AOB的度数。
O
A
B
.
A
O
B
E
C
D
F
思考题
已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
问题?
O
A
B
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
问题?
O
A
B
D
C
r
应用:
O
A
B
D
C
r
如图用 表示主桥拱,设 所在圆的圆心为O,半径为r.
经过圆心O作弦AB的垂线OC,D为垂足,OC与 相交于点C,根据前面的结论,D是AB的中点,C是 的中点,CD就是拱高.
在图中,
因此,赵州桥的主桥拱半径约为27.9m.
垂径定理的应用
1、在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度.
驶向胜利的彼岸
E
D
┌
600
B
A
O
600
650
D
C
船能过拱桥吗
2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
相信自己能独立完成解答.
驶向胜利的彼岸
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
驶向胜利的彼岸
在Rt△OAD中,由勾股定理,得
解得 R≈3.9(m).
在Rt△ONH中,由勾股定理,得
∴此货船能顺利通过这座拱桥.
24.1.2 垂直于弦的直径
学海中学
教学目标:
1.会利用圆的轴对称性探究垂径定理、证明垂径定理;
2.能利用垂径定理进行相关的计算和证明;
3、掌握垂径定理的推论:圆的两条平行弦所夹的弧相等.
教学重点:
垂径定理的证明与简单应用;
教学难点:
垂径定理的证明定理及其简单应用;
结 论:圆是轴对称图形。
经过圆心的每一条直线都是它的对称轴。
特殊性:对称轴有无数条。
③AM=BM,
AB是⊙O的一条弦.
又有何结论
驶向胜利的彼岸
作直径CD,使CD⊥AB,垂足为M.
●O
我们发现图中有:
A
B
C
D
M└
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理
定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
驶向胜利的彼岸
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
你可以写出相应的结论吗
垂径定理的逆定理
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
驶向胜利的彼岸
●O
A
B
C
D
M└
③ CD是直径,
AM=BM,
① CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
②
垂径定理及其推论.
垂径定理:垂直于弦的直径平分弦,并且平分弦
所对的两条弧.
推论1:平分弦(不是直径)的直径垂直于弦,并且
平分弦所对的两条弧.
推论2:弦的垂直平分线经过圆心,并且平分弦
所对的两条弧.
推论3:平分弦所对的一条弧的直径,垂直平分
弦,并平分弦所对的另一条弧.
驶向胜利的彼岸
挑战自我画一画
如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
试一试P93
12
驶向胜利的彼岸
挑战自我填一填
判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条平行弦所夹的弧相等. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )
B
A
O
应用:
已知如图,在 中,弦AB的长为8cm,若圆心O到AB的距离为3 cm,则 的半径为 cm.
C
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题.
5
例2、如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
求证:AC = BD
A
B
C
D
O
E
证明:过O作OE⊥AB,垂足为E, 则AE = BE, CE = DE
∴AE - CE = BE - DE
即 AC = BD
辅助线:垂直于弦的直径。 实际上从圆心作与弦垂直的线段。
练习
变 换
A
B
C
D
O
1、如图1,在⊙O中, AB是 弦, OC = OD。
求证:AC = BD
(1)
A
B
C
D
O
2、如图2,在⊙O中, CD是
弦, OA = OB。
求证:AC = BD
(2)
2.已知:如图,在⊙O中,AB、AC为互相垂直的两条相等的弦,OD⊥AB,OE⊥AC,D、E为垂足。求证:ADOE为正方形。
O
A
B
C
D
E
练习
1. 在半径为50mm的⊙O中,有长50mm的弦AB。计算:
(1) 点O与AB的距离;
(2)∠AOB的度数。
O
A
B
.
A
O
B
E
C
D
F
思考题
已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
问题?
O
A
B
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
问题?
O
A
B
D
C
r
应用:
O
A
B
D
C
r
如图用 表示主桥拱,设 所在圆的圆心为O,半径为r.
经过圆心O作弦AB的垂线OC,D为垂足,OC与 相交于点C,根据前面的结论,D是AB的中点,C是 的中点,CD就是拱高.
在图中,
因此,赵州桥的主桥拱半径约为27.9m.
垂径定理的应用
1、在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度.
驶向胜利的彼岸
E
D
┌
600
B
A
O
600
650
D
C
船能过拱桥吗
2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
相信自己能独立完成解答.
驶向胜利的彼岸
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
驶向胜利的彼岸
在Rt△OAD中,由勾股定理,得
解得 R≈3.9(m).
在Rt△ONH中,由勾股定理,得
∴此货船能顺利通过这座拱桥.
同课章节目录
