(北京版)小学数学毕业复习空间观念复习建议
文档属性
| 名称 | (北京版)小学数学毕业复习空间观念复习建议 |  | |
| 格式 | rar | ||
| 文件大小 | 374.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-09 10:57:50 | ||
图片预览








文档简介
(共55张PPT)
空间观念
复习建议
几何初步知识总复习建议
一.几何知识是小学数学学习的重要内容
二.小学几何教学是中学数学学习的基础
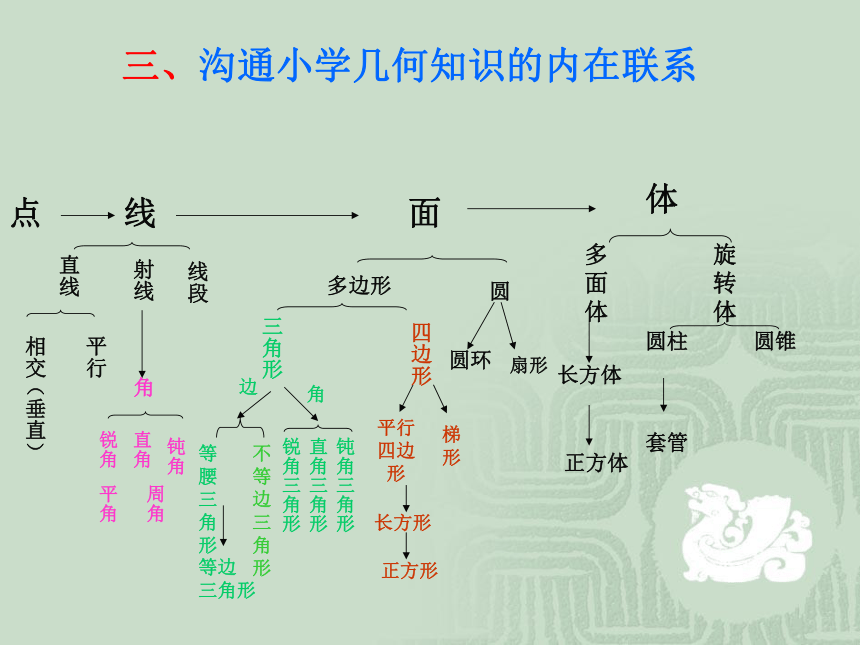
三.沟通小学几何知识的内在联系
四.掌握小学几何知识的思想方法
五.解决小学几何知识的典型题目
一、几何知识是小学数学学习的重要内容
几何知识的教学是运用实物、图形等直观教具、学具,让学生通过观察、分析、比较来发现几何形体的特征,掌握有关的知识。重视直观教学,加强动手操作,发展学生的空间观念,是几何教学的重要规律。
二、小学几何教学是中学数学学习的基础
1 .小学已经出现的平面图形的有关计算公式,初中不再作为新知识重新出现.
2.小学已经出现过的某些几何概念,初中将重新表述,但与小学教材里的表述没有本质上的差异。
如平行线的定义,初中和小学都说:“在同一平面内,不相交的两条直线叫做平行线。”而梯形的定义,小学表述为“只有一组对边平行的四边形叫做梯形”。初中则表述为“一组对边平行而另一组对边不平行的四边形叫做梯形”。尽管在表述句式上略有不同,但没有本质上的差异。
4.小学里已经出现过的性质、定理,因为缺乏理论依据,初中将加以推理证明。
3.小学里已经出现过的某些几何概念,初中将重新表述,且与小学的表述有本质上的差异。
如小学里三角形的定义表述为“由三条线段围成的图形,这样的图形叫做三角形”。“围成”不能确切地表示“首尾连接”,因为交叉,重叠也能是围成。初中则表述为“由不在同一直线上的三条线段首尾顺次连接所组成的图形叫做三角形”。“不在同一直线上”与“首尾顺次连接”都突出了三角形定义上的本质属性。
三、沟通小学几何知识的内在联系
等边
三角形
边
正方形
角
圆环
相交
角
平行
(垂直)
直线
射线
线段
直角
钝角
平角
锐角
周角
点
线
面
体
圆
三角形
四边形
等
腰
三
角
形
锐角三角形
直角三角形
钝角三角形
平行
四边形
长方形
梯
形
旋
转
体
圆柱
套管
长方体
正方体
多
面
体
圆锥
多边形
不等边三角形
扇形
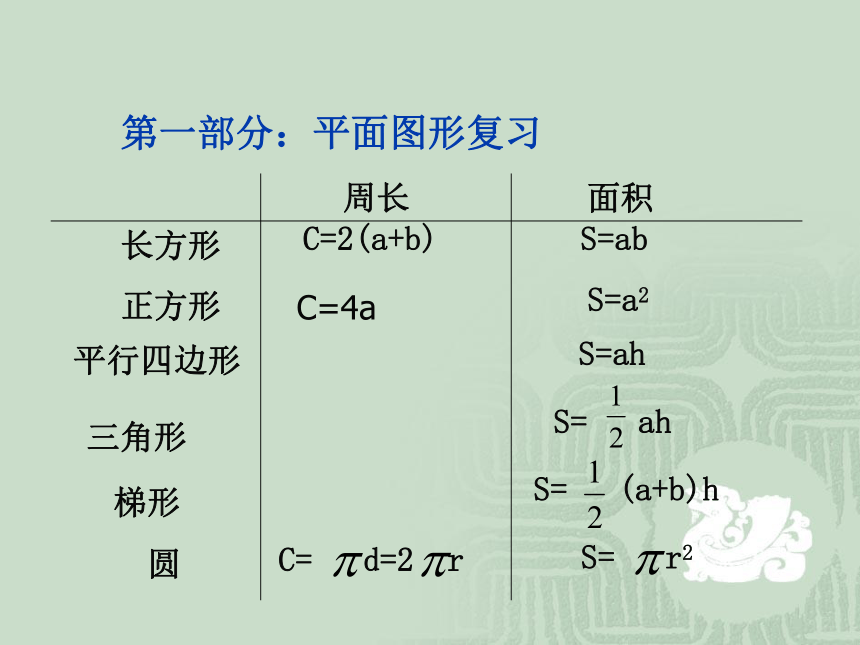
第一部分:平面图形复习
圆
C= d=2 r
S= r2
S= (a+b)h
周长
面积
长方形
C=2(a+b)
S=ab
正方形
S=a2
平行四边形
S=ah
三角形
S= ah
梯形
C=4a
S=∏r2
S=ab
S=a2
S= ah
s= (a+b)h
S=ah
πr
r
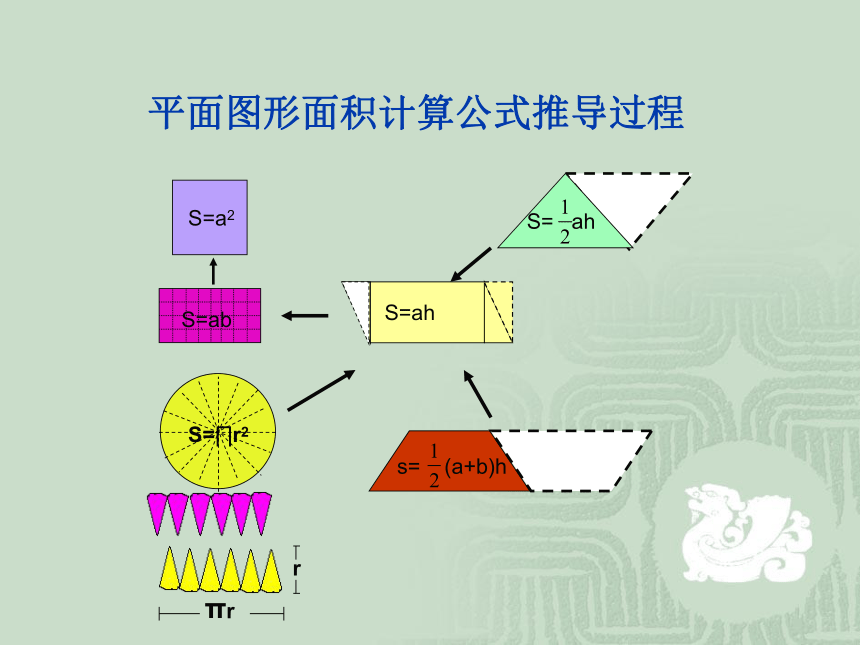
平面图形面积计算公式推导过程
S= (a+b)h
S= ah
S=ah
S=ab(h)
S=a2
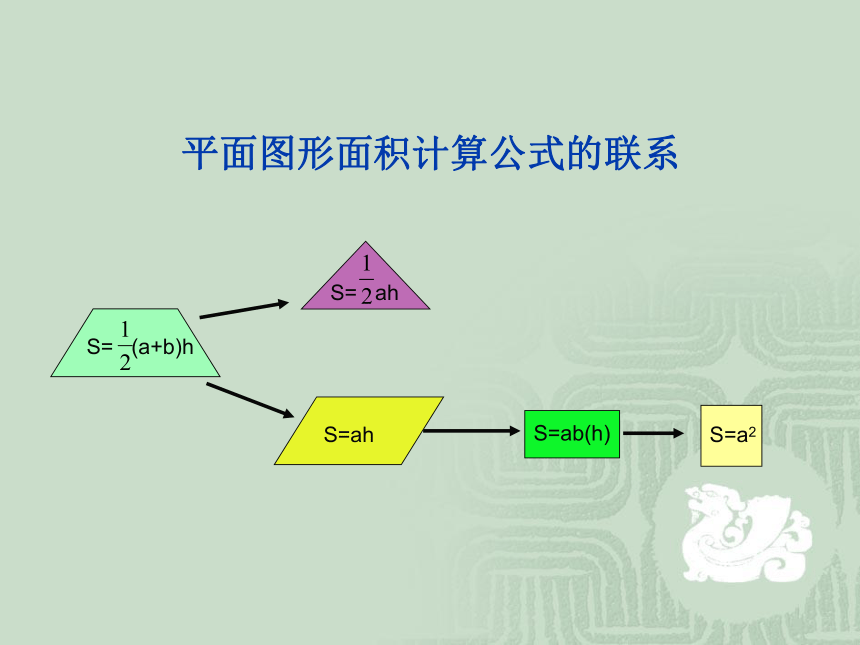
平面图形面积计算公式的联系
安排如下活动,可以进一步帮助复习。
1.在方格纸上,画周长为12.56的平面图形,看哪个组画的多。 2.你能计算它们的面积吗? 3.小组交流,你们还发现了什么?
可能出现情况
1.画圆形,半径为2,唯一一种画法,面积为12.56。 2.画长方形,根据长和宽不同情况可以有许多种不同情况,但它们长宽的和一定是6.28。会发现,长和宽越接近,面积越大;长和宽相等时,面积最大。 3.画三角形,应满足两边之和大于第三边的基本条件。如果画一般三角形,不易求出面积,因不知道三角形的高;如果画直角三角形,需考虑是否符合勾股定理。 4.画平行四边形,易画而不知道高,不易求出面积。 5.画梯形,如果画一般梯形,不易求出面积,因不知道梯形的高;如果画直角梯形,需考虑是否符合勾股定理。
o
r=2
r:12.56÷2÷ =2
S:22× =12.56
3.14
3.14
5.28
1
3
2
4.28
3.28
1×5.28=5.28
2×4.28=8.56
3.14×3.14=9.8596
3×3.28=9.84
4.28
2
普通平行四边形易画而不知道高,不易求出面积。
4.98
1.3
1.2
0.5
4.48
这个平行四边形符合勾股定理:0.52+1.22=1.32
4.98×1.2=5.976
5
3
2
2.56
如果画一般梯形,不易求出面积,因不知道梯形的高。
3
3
0.28
4.28
5
这个梯形符合勾股定理:
32+42=52
(4.28+0.28)×3÷2=6.84
1.棱长总和:长方体,正方体都有12条棱
2.表面积: 长方体:S长=(ab+ac+bc)×2
正方体:S正=6a2
圆柱:S侧 =C底h
S表 = S侧+2S底
(=S侧+S底)
第二部分:立体图形复习
3.体积:
V长=abh=Sh
V正=a3=Sh
V长=Sh
V圆柱=S底h
S底h
V锥=
C圆
h
C圆
h
r
r÷2
圆柱体表面积=底面周长×(高+半径)
当无盖(或底)时所需材料面积
底面周长×(高+ 半径)
圆柱表面积计算方法(补充)
C长方形
C正方形
C圆
h
h
h
C三角形
h
……
……
S侧=Ch
直柱体侧面积
直柱体表面积
=侧面积+2倍底面积
直柱体侧面积和表面积
V=abh
V=a3
V=sh
V=sh
直柱体
……
直柱体体积
三棱柱:V=sh
四棱柱:V=sh
等底等高时
V柱= 3V锥
V锥= V柱
等底等体积时
h锥= 3h柱
h柱= h锥
圆柱与圆锥底面积、高、体积之间的关系
等高等体积时
s锥= 3s柱
s柱= s锥
如左图所示,圆锥的高是圆
柱的 ,圆柱与圆锥底面积
的比是5:4,圆锥的体积是圆
柱的 。
可以按份列表来解答问题
2
5
4
高
底面积
体积
圆柱
圆锥
3
15
÷15 =
四、掌握小学几何知识的思想方法
1.渗透数形结合思想。
某部队有解放军战士若干人,正好排成一个方阵,若将此方阵改排成长方阵,因而减少6行,同时各行均增加10人。问战士人数是多少?
解:设原方阵每行x人。
6x=10(x-6)
6x=10x-60
4x=60
x=15
15×15=225(人)
2.渗透分类思想
分类就是把所研究的问题按照某种标准分成若干种情况,然后分情况解决问题,使整个问题得到解决。小学几何中已学过分类的问题,如三角形按角分,可分为锐角三角形、直角三角形、钝角三角形。
直角三角形
锐角三角形
钝角三角形
三角形按角分类
3.渗透转化思想
在研究数学问题时,将未解决的问题转化成已解决的问题,将复杂的问题转化成简单的问题,将数量问题转化成图形问题或将图形问题转化成数量问题等等,这样的一种思想称为转化思想。
解法:16×2÷8=4(cm)
利用转化的思想解决问题
例2:下图长方形中黄色部分面积为a平方厘米,求长方形面积。
S阴影=
S长方形
解答:因为长方形是黄色面积的2倍,所以用a×2=2a平方厘米。
在一个底面半径是10厘米的圆柱形状的容器中装着一些水,水里放了一个底面半径5厘米的圆锥形状的铅锤。当铅锤从容器中取出后,容器中水面下降5毫米。铅锤的高是多少厘米?
10cm
5mm
正确列式:(102×3.14×0.5×3)÷(3.14×52)
错例1:(102×3.14×0.5)÷(3.14×52)
错例2:(102×3.14×5×3)÷(3.14×52)
等积变形
例3:
列方程解:设铅锤的高x厘米。
×52 x=102 ×0.5
一只装有水的圆柱形玻璃杯,底面积是80平方厘米,水深8厘米。现将一个底面积是16平方厘米的长方体铁块竖放在水中后,仍有一部分铁块露在外面。现在的水深多少厘米?
解法一:
80×8÷(80-16)
=640 ÷64
=10(厘米)
解法二:设水面上升x厘米。
80x=16×(8+x)
80x=128+16x
64x=128
x=2
8+2=10(厘米)
例4:
4 、渗透归纳思想
研究一般性问题时,在观察和实验的基础上,归纳出由特殊现象到一般现象的规律和性质,这种从特殊到一般的思维方式称为归纳思想。
C长方形
C正方形
C圆
h
h
h
C三角形
h
……
……
S侧=Ch
直柱体侧面积
直柱体表面积
=侧面积+2倍底面积
直柱体侧面积和表面积
V=abh
V=a3
V=sh
V=sh
直柱体
……
直柱体体积
五、解决小学几何知识的典型题目
1.正方形与圆
2.最大与最小
3.正方体所有可能的截面类型
4.立体图形的切割与拼合
5 .杂题
圆的半径扩大(或缩小)a倍,直径和周长也随着扩大(或缩小)a倍,而圆的面积则扩大(或缩小)a2倍。
圆的半径与直径、周长成正比例,半径与面积不成比例。
正方形的边长扩大(或缩小)a倍,周长也扩大(或缩小)a倍,而面积扩大(或缩小)a2倍。
正方形边长与周长成正比例,边长与面积不成比例。
1.正方形与圆
S圆= S正方形
S正方形= S圆
S圆= S正方形
S正方形= S圆
S圆= S正方形
S正方形= S圆
图解:
独立思考,认真观察,下面图形中哪个阴影部分的面积大?(每个正方形边长相等)
(1)
(2)
(3)
(4)
(5)
(6)
2.最大与最小
40cm
20cm
指定深度为5厘米
例1:下图是一张长40厘米,宽20厘米的长方形铁板,要把这张铁板焊一个深5厘米的盒子(无盖),让这个长方形铁盒的容积有三种大小不同的规格,应该怎样设计与使用这块铁板?
容积最大
……
解:20×20×5
=2000(平方厘米)
解:30×10×5
=1500(平方厘米)
解:35×10×5
=1750(平方厘米)
分析与解:
甲圆柱的底面半径为5厘米,高10厘米。乙圆柱底面半径10厘米,高5厘米。这两个圆柱的表面积谁大?大的表面积是小的表面积的多少倍?
解法一:利用所给条件分别求出两个 圆柱的表面积,再求倍数关系。
5
10
5
10
甲
乙
解法二:S甲表:S乙表
=2 r甲( h甲+ r甲): 2 r乙( h乙+ r乙)
= r甲( h甲+ r甲) : r乙( h乙+ r乙)
=r甲: r乙
= 5 :10 =1 : 2
例2
截面面积最小
12
24
4
12
24
4
截面面积最大
12
24
4
12
24
4
(单位:厘米)
长方体垂直于长、宽、高的截面
例3:要把3本长20厘米、宽12厘米、高6厘米的《现代汉语词典》包装起来,至少要准备多少平方厘米的包装纸?(重合处不计)
分析:只要使长方体物体最大的面重合,就能使包装纸的表
面积最小。
① 用3个长方体的表面积总和减去4个重合面面积。 (20×12+20×6+12×6)×2×3-20×12×4
② 20×12×2+(20×6+12×6)×2×3
正方体的截面中,不可能出现直角三角形、钝角三角形,可能出现锐角三角形、等边或等腰三角形
3.正方体所有可能的截面类型
可能出现正方形、矩形
不可能出现非矩形的平行四边形及直角梯形,可能出现等腰梯形
可能出现五边形,不可能出现正五边形
可能出现正六边形及六边形
不可能出现七边形及多于七边的多边形
研究者——北大附中学生:王明天 陆程遂
长方形
正方形
圆
椭圆
4.立体图形的切割
三角形
圆 柱
长方体
圆锥
圆
截成圆锥和圆台
6
把两个底面半径2厘米,高10厘米的圆柱拼成一个大圆柱,表面积增加了多少平方厘米?
将一个底面直径12厘米,高4厘米的圆柱形木料沿底面直径和高,从上到下劈成相等的两块(如图),每块木料的表面积是多少平方厘米?
6
2
将一块圆柱形状的木料如下图劈开,拼成了一个近似的长方体。这个近似长方体的表面积是多少平方分米?
立体图形的切拼实例
从一个棱长10厘米的正方体木块上截去一个棱长2厘米的小正方体,剩下的表面积是多少平方厘米?
正方体切割
表面积不变
10×10×6
表面积多了2个小正方形的面积
10×10×6+2×2×2
表面积多了4个小正方形的面积
10×10×6+2×2×4
在 复行”概念:在同一平面内,两条永不相交的直线互相平行。老师 可以出示下列几组变式让学生去分辨并感知:
例4:运用变式,把握实质
让学生说说,三幅图中线a与线b是否平行,为什么?通过这组变式练习,我相信学生有可能真正领会“平行”的实质了。
例1:小洁给妈妈买了一件生日礼物。礼品的包装盒长25厘米,宽10厘米,高4厘米。售货员用丝带如图这样进行捆扎,做蝴蝶结用了15厘米。捆扎用的丝带全长多少厘米?
25
10
4
25×2+10×4+4×6+15
5 . 杂题
解法一:空圆柱容积+装有液体的圆柱容积=瓶子的容积。
3.14×52×(36 -30)+3.14×52×24
解法二:空圆柱与装有液体的圆柱等底,将它们拼在一起,成为一个底面直径10厘米,高为30厘米—(36-30+24)的圆柱体,求出这个圆柱体的容积,就计算出了瓶子的容积。
3.14×52×(36-30+24)
半径 10÷2=5(厘米)
30
24
36
(单位:厘米)
10
例2:瓶子的容积是多少?
解法四:与上面想法类似,可以求出空圆柱的容积
后再乘5——24÷6+1 ,就可以得到瓶子的容积。
30
24
36
(单位:厘米)
10
3.14×52×(36-30)×(4+1)
解法三:先求出空圆柱的高——6厘米,在等底的情况下,6厘米是24厘米的几分之几,那么高为6厘米的圆柱的容积就是高为24厘米的圆柱容积的几分之几。因此求出左图的圆柱容积后再加上这个容积的 就可以了。
3.14×52×24×(1+ )
其他解法略
长方形周长40厘米,长与宽的比为3:1,这个长方形的面积是多少?
长方体棱长总和120厘米,长、宽、高的比为3:2:1,这个长方体的体积是多少立方厘米?
错例:(40 × )
× (40 × )
错例:120×
120×
120×
……
例3:周长、棱长总和与各边之比
空间观念
复习建议
几何初步知识总复习建议
一.几何知识是小学数学学习的重要内容
二.小学几何教学是中学数学学习的基础
三.沟通小学几何知识的内在联系
四.掌握小学几何知识的思想方法
五.解决小学几何知识的典型题目
一、几何知识是小学数学学习的重要内容
几何知识的教学是运用实物、图形等直观教具、学具,让学生通过观察、分析、比较来发现几何形体的特征,掌握有关的知识。重视直观教学,加强动手操作,发展学生的空间观念,是几何教学的重要规律。
二、小学几何教学是中学数学学习的基础
1 .小学已经出现的平面图形的有关计算公式,初中不再作为新知识重新出现.
2.小学已经出现过的某些几何概念,初中将重新表述,但与小学教材里的表述没有本质上的差异。
如平行线的定义,初中和小学都说:“在同一平面内,不相交的两条直线叫做平行线。”而梯形的定义,小学表述为“只有一组对边平行的四边形叫做梯形”。初中则表述为“一组对边平行而另一组对边不平行的四边形叫做梯形”。尽管在表述句式上略有不同,但没有本质上的差异。
4.小学里已经出现过的性质、定理,因为缺乏理论依据,初中将加以推理证明。
3.小学里已经出现过的某些几何概念,初中将重新表述,且与小学的表述有本质上的差异。
如小学里三角形的定义表述为“由三条线段围成的图形,这样的图形叫做三角形”。“围成”不能确切地表示“首尾连接”,因为交叉,重叠也能是围成。初中则表述为“由不在同一直线上的三条线段首尾顺次连接所组成的图形叫做三角形”。“不在同一直线上”与“首尾顺次连接”都突出了三角形定义上的本质属性。
三、沟通小学几何知识的内在联系
等边
三角形
边
正方形
角
圆环
相交
角
平行
(垂直)
直线
射线
线段
直角
钝角
平角
锐角
周角
点
线
面
体
圆
三角形
四边形
等
腰
三
角
形
锐角三角形
直角三角形
钝角三角形
平行
四边形
长方形
梯
形
旋
转
体
圆柱
套管
长方体
正方体
多
面
体
圆锥
多边形
不等边三角形
扇形
第一部分:平面图形复习
圆
C= d=2 r
S= r2
S= (a+b)h
周长
面积
长方形
C=2(a+b)
S=ab
正方形
S=a2
平行四边形
S=ah
三角形
S= ah
梯形
C=4a
S=∏r2
S=ab
S=a2
S= ah
s= (a+b)h
S=ah
πr
r
平面图形面积计算公式推导过程
S= (a+b)h
S= ah
S=ah
S=ab(h)
S=a2
平面图形面积计算公式的联系
安排如下活动,可以进一步帮助复习。
1.在方格纸上,画周长为12.56的平面图形,看哪个组画的多。 2.你能计算它们的面积吗? 3.小组交流,你们还发现了什么?
可能出现情况
1.画圆形,半径为2,唯一一种画法,面积为12.56。 2.画长方形,根据长和宽不同情况可以有许多种不同情况,但它们长宽的和一定是6.28。会发现,长和宽越接近,面积越大;长和宽相等时,面积最大。 3.画三角形,应满足两边之和大于第三边的基本条件。如果画一般三角形,不易求出面积,因不知道三角形的高;如果画直角三角形,需考虑是否符合勾股定理。 4.画平行四边形,易画而不知道高,不易求出面积。 5.画梯形,如果画一般梯形,不易求出面积,因不知道梯形的高;如果画直角梯形,需考虑是否符合勾股定理。
o
r=2
r:12.56÷2÷ =2
S:22× =12.56
3.14
3.14
5.28
1
3
2
4.28
3.28
1×5.28=5.28
2×4.28=8.56
3.14×3.14=9.8596
3×3.28=9.84
4.28
2
普通平行四边形易画而不知道高,不易求出面积。
4.98
1.3
1.2
0.5
4.48
这个平行四边形符合勾股定理:0.52+1.22=1.32
4.98×1.2=5.976
5
3
2
2.56
如果画一般梯形,不易求出面积,因不知道梯形的高。
3
3
0.28
4.28
5
这个梯形符合勾股定理:
32+42=52
(4.28+0.28)×3÷2=6.84
1.棱长总和:长方体,正方体都有12条棱
2.表面积: 长方体:S长=(ab+ac+bc)×2
正方体:S正=6a2
圆柱:S侧 =C底h
S表 = S侧+2S底
(=S侧+S底)
第二部分:立体图形复习
3.体积:
V长=abh=Sh
V正=a3=Sh
V长=Sh
V圆柱=S底h
S底h
V锥=
C圆
h
C圆
h
r
r÷2
圆柱体表面积=底面周长×(高+半径)
当无盖(或底)时所需材料面积
底面周长×(高+ 半径)
圆柱表面积计算方法(补充)
C长方形
C正方形
C圆
h
h
h
C三角形
h
……
……
S侧=Ch
直柱体侧面积
直柱体表面积
=侧面积+2倍底面积
直柱体侧面积和表面积
V=abh
V=a3
V=sh
V=sh
直柱体
……
直柱体体积
三棱柱:V=sh
四棱柱:V=sh
等底等高时
V柱= 3V锥
V锥= V柱
等底等体积时
h锥= 3h柱
h柱= h锥
圆柱与圆锥底面积、高、体积之间的关系
等高等体积时
s锥= 3s柱
s柱= s锥
如左图所示,圆锥的高是圆
柱的 ,圆柱与圆锥底面积
的比是5:4,圆锥的体积是圆
柱的 。
可以按份列表来解答问题
2
5
4
高
底面积
体积
圆柱
圆锥
3
15
÷15 =
四、掌握小学几何知识的思想方法
1.渗透数形结合思想。
某部队有解放军战士若干人,正好排成一个方阵,若将此方阵改排成长方阵,因而减少6行,同时各行均增加10人。问战士人数是多少?
解:设原方阵每行x人。
6x=10(x-6)
6x=10x-60
4x=60
x=15
15×15=225(人)
2.渗透分类思想
分类就是把所研究的问题按照某种标准分成若干种情况,然后分情况解决问题,使整个问题得到解决。小学几何中已学过分类的问题,如三角形按角分,可分为锐角三角形、直角三角形、钝角三角形。
直角三角形
锐角三角形
钝角三角形
三角形按角分类
3.渗透转化思想
在研究数学问题时,将未解决的问题转化成已解决的问题,将复杂的问题转化成简单的问题,将数量问题转化成图形问题或将图形问题转化成数量问题等等,这样的一种思想称为转化思想。
解法:16×2÷8=4(cm)
利用转化的思想解决问题
例2:下图长方形中黄色部分面积为a平方厘米,求长方形面积。
S阴影=
S长方形
解答:因为长方形是黄色面积的2倍,所以用a×2=2a平方厘米。
在一个底面半径是10厘米的圆柱形状的容器中装着一些水,水里放了一个底面半径5厘米的圆锥形状的铅锤。当铅锤从容器中取出后,容器中水面下降5毫米。铅锤的高是多少厘米?
10cm
5mm
正确列式:(102×3.14×0.5×3)÷(3.14×52)
错例1:(102×3.14×0.5)÷(3.14×52)
错例2:(102×3.14×5×3)÷(3.14×52)
等积变形
例3:
列方程解:设铅锤的高x厘米。
×52 x=102 ×0.5
一只装有水的圆柱形玻璃杯,底面积是80平方厘米,水深8厘米。现将一个底面积是16平方厘米的长方体铁块竖放在水中后,仍有一部分铁块露在外面。现在的水深多少厘米?
解法一:
80×8÷(80-16)
=640 ÷64
=10(厘米)
解法二:设水面上升x厘米。
80x=16×(8+x)
80x=128+16x
64x=128
x=2
8+2=10(厘米)
例4:
4 、渗透归纳思想
研究一般性问题时,在观察和实验的基础上,归纳出由特殊现象到一般现象的规律和性质,这种从特殊到一般的思维方式称为归纳思想。
C长方形
C正方形
C圆
h
h
h
C三角形
h
……
……
S侧=Ch
直柱体侧面积
直柱体表面积
=侧面积+2倍底面积
直柱体侧面积和表面积
V=abh
V=a3
V=sh
V=sh
直柱体
……
直柱体体积
五、解决小学几何知识的典型题目
1.正方形与圆
2.最大与最小
3.正方体所有可能的截面类型
4.立体图形的切割与拼合
5 .杂题
圆的半径扩大(或缩小)a倍,直径和周长也随着扩大(或缩小)a倍,而圆的面积则扩大(或缩小)a2倍。
圆的半径与直径、周长成正比例,半径与面积不成比例。
正方形的边长扩大(或缩小)a倍,周长也扩大(或缩小)a倍,而面积扩大(或缩小)a2倍。
正方形边长与周长成正比例,边长与面积不成比例。
1.正方形与圆
S圆= S正方形
S正方形= S圆
S圆= S正方形
S正方形= S圆
S圆= S正方形
S正方形= S圆
图解:
独立思考,认真观察,下面图形中哪个阴影部分的面积大?(每个正方形边长相等)
(1)
(2)
(3)
(4)
(5)
(6)
2.最大与最小
40cm
20cm
指定深度为5厘米
例1:下图是一张长40厘米,宽20厘米的长方形铁板,要把这张铁板焊一个深5厘米的盒子(无盖),让这个长方形铁盒的容积有三种大小不同的规格,应该怎样设计与使用这块铁板?
容积最大
……
解:20×20×5
=2000(平方厘米)
解:30×10×5
=1500(平方厘米)
解:35×10×5
=1750(平方厘米)
分析与解:
甲圆柱的底面半径为5厘米,高10厘米。乙圆柱底面半径10厘米,高5厘米。这两个圆柱的表面积谁大?大的表面积是小的表面积的多少倍?
解法一:利用所给条件分别求出两个 圆柱的表面积,再求倍数关系。
5
10
5
10
甲
乙
解法二:S甲表:S乙表
=2 r甲( h甲+ r甲): 2 r乙( h乙+ r乙)
= r甲( h甲+ r甲) : r乙( h乙+ r乙)
=r甲: r乙
= 5 :10 =1 : 2
例2
截面面积最小
12
24
4
12
24
4
截面面积最大
12
24
4
12
24
4
(单位:厘米)
长方体垂直于长、宽、高的截面
例3:要把3本长20厘米、宽12厘米、高6厘米的《现代汉语词典》包装起来,至少要准备多少平方厘米的包装纸?(重合处不计)
分析:只要使长方体物体最大的面重合,就能使包装纸的表
面积最小。
① 用3个长方体的表面积总和减去4个重合面面积。 (20×12+20×6+12×6)×2×3-20×12×4
② 20×12×2+(20×6+12×6)×2×3
正方体的截面中,不可能出现直角三角形、钝角三角形,可能出现锐角三角形、等边或等腰三角形
3.正方体所有可能的截面类型
可能出现正方形、矩形
不可能出现非矩形的平行四边形及直角梯形,可能出现等腰梯形
可能出现五边形,不可能出现正五边形
可能出现正六边形及六边形
不可能出现七边形及多于七边的多边形
研究者——北大附中学生:王明天 陆程遂
长方形
正方形
圆
椭圆
4.立体图形的切割
三角形
圆 柱
长方体
圆锥
圆
截成圆锥和圆台
6
把两个底面半径2厘米,高10厘米的圆柱拼成一个大圆柱,表面积增加了多少平方厘米?
将一个底面直径12厘米,高4厘米的圆柱形木料沿底面直径和高,从上到下劈成相等的两块(如图),每块木料的表面积是多少平方厘米?
6
2
将一块圆柱形状的木料如下图劈开,拼成了一个近似的长方体。这个近似长方体的表面积是多少平方分米?
立体图形的切拼实例
从一个棱长10厘米的正方体木块上截去一个棱长2厘米的小正方体,剩下的表面积是多少平方厘米?
正方体切割
表面积不变
10×10×6
表面积多了2个小正方形的面积
10×10×6+2×2×2
表面积多了4个小正方形的面积
10×10×6+2×2×4
在 复行”概念:在同一平面内,两条永不相交的直线互相平行。老师 可以出示下列几组变式让学生去分辨并感知:
例4:运用变式,把握实质
让学生说说,三幅图中线a与线b是否平行,为什么?通过这组变式练习,我相信学生有可能真正领会“平行”的实质了。
例1:小洁给妈妈买了一件生日礼物。礼品的包装盒长25厘米,宽10厘米,高4厘米。售货员用丝带如图这样进行捆扎,做蝴蝶结用了15厘米。捆扎用的丝带全长多少厘米?
25
10
4
25×2+10×4+4×6+15
5 . 杂题
解法一:空圆柱容积+装有液体的圆柱容积=瓶子的容积。
3.14×52×(36 -30)+3.14×52×24
解法二:空圆柱与装有液体的圆柱等底,将它们拼在一起,成为一个底面直径10厘米,高为30厘米—(36-30+24)的圆柱体,求出这个圆柱体的容积,就计算出了瓶子的容积。
3.14×52×(36-30+24)
半径 10÷2=5(厘米)
30
24
36
(单位:厘米)
10
例2:瓶子的容积是多少?
解法四:与上面想法类似,可以求出空圆柱的容积
后再乘5——24÷6+1 ,就可以得到瓶子的容积。
30
24
36
(单位:厘米)
10
3.14×52×(36-30)×(4+1)
解法三:先求出空圆柱的高——6厘米,在等底的情况下,6厘米是24厘米的几分之几,那么高为6厘米的圆柱的容积就是高为24厘米的圆柱容积的几分之几。因此求出左图的圆柱容积后再加上这个容积的 就可以了。
3.14×52×24×(1+ )
其他解法略
长方形周长40厘米,长与宽的比为3:1,这个长方形的面积是多少?
长方体棱长总和120厘米,长、宽、高的比为3:2:1,这个长方体的体积是多少立方厘米?
错例:(40 × )
× (40 × )
错例:120×
120×
120×
……
例3:周长、棱长总和与各边之比
