鲁教五四新版 七年级数学上册 第3章 勾股定理 单元测试卷 (word版,含解析)
文档属性
| 名称 | 鲁教五四新版 七年级数学上册 第3章 勾股定理 单元测试卷 (word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 862.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-25 06:00:43 | ||
图片预览


文档简介
第3章 勾股定理 单元测试卷
一、选择题(共8小题).
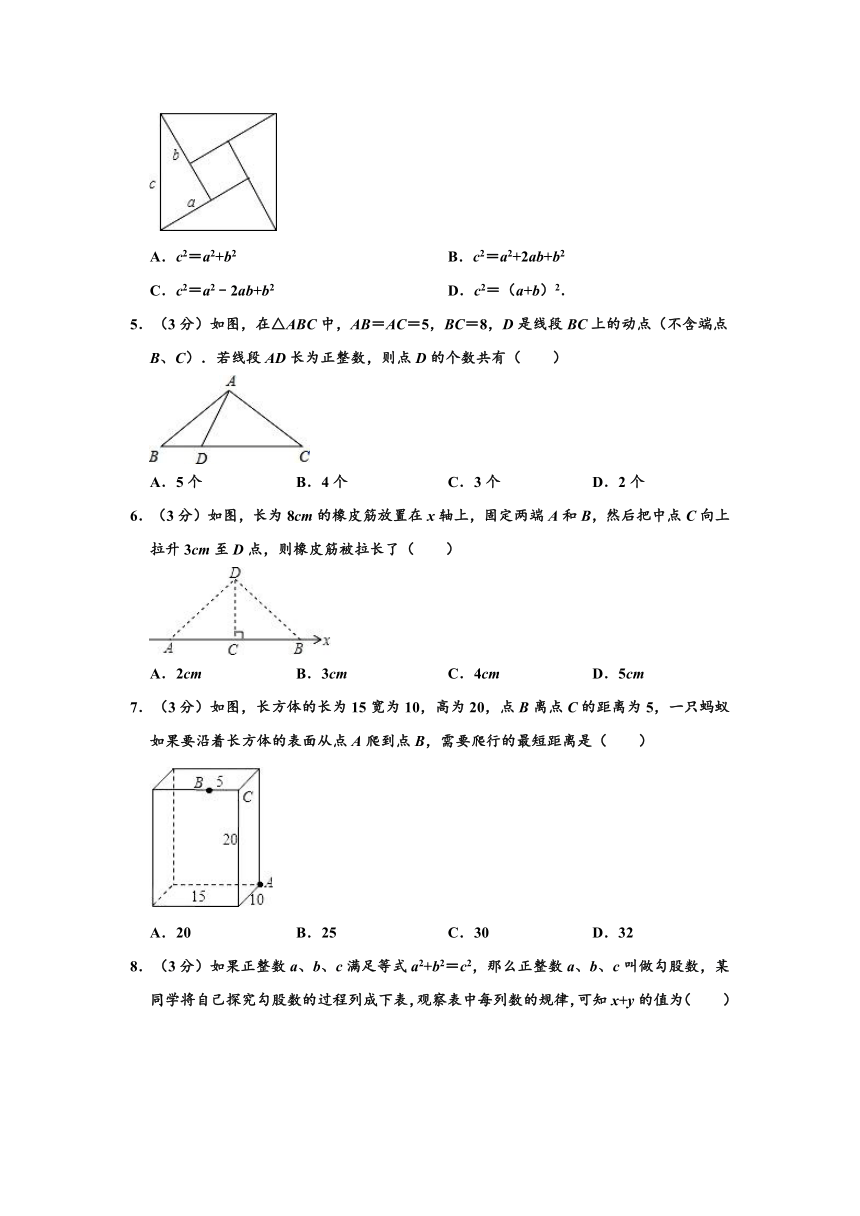
1.(3分)勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A. B. C. D.
2.(3分)如图中,边长k等于5的直角三角形有( )
A.1个 B.2个 C.3个 D.4个
3.(3分)五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
4.(3分)用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
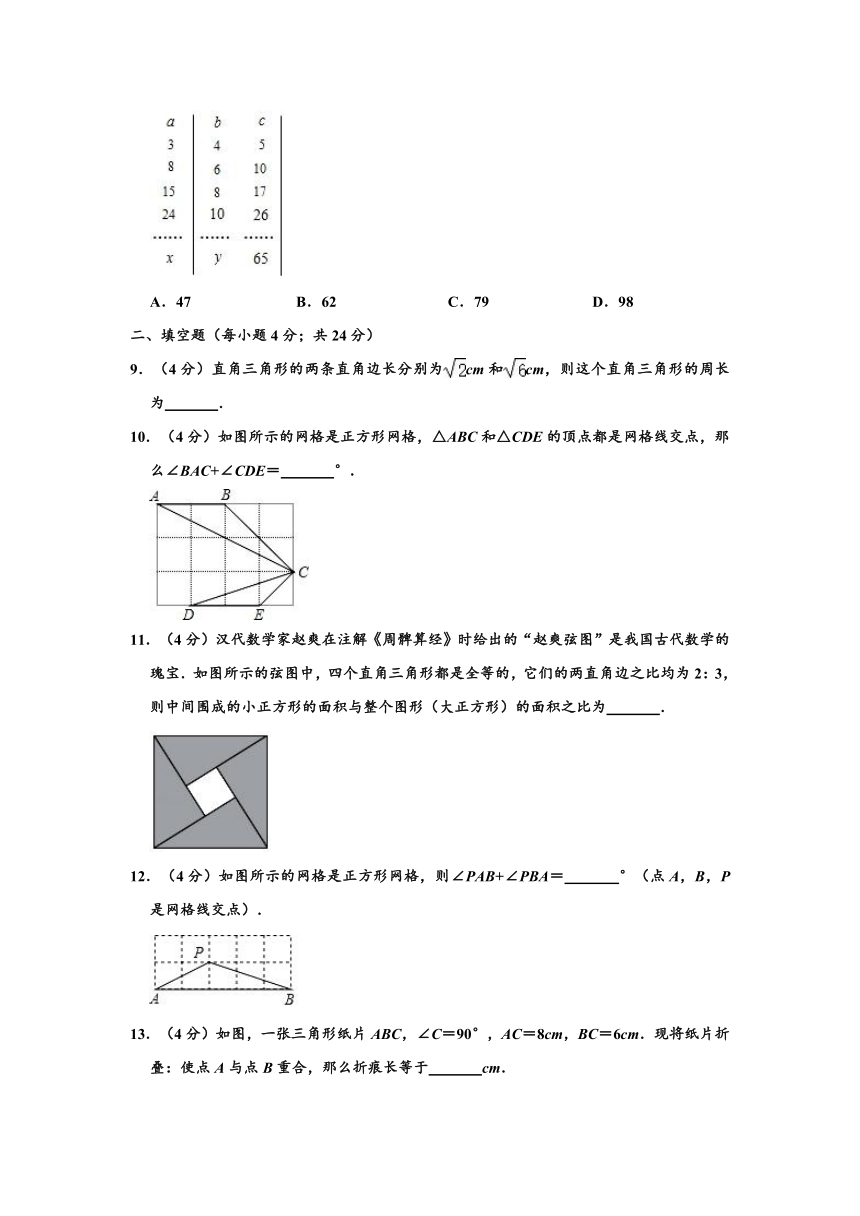
C.c2=a2﹣2ab+b2 D.c2=(a+b)2.
5.(3分)如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
6.(3分)如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了( )
A.2cm B.3cm C.4cm D.5cm
7.(3分)如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.20 B.25 C.30 D.32
8.(3分)如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
二、填空题(每小题4分;共24分)
9.(4分)直角三角形的两条直角边长分别为cm和cm,则这个直角三角形的周长为 .
10.(4分)如图所示的网格是正方形网格,△ABC和△CDE的顶点都是网格线交点,那么∠BAC+∠CDE= °.
11.(4分)汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2:3,则中间围成的小正方形的面积与整个图形(大正方形)的面积之比为 .
12.(4分)如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
13.(4分)如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于 cm.
14.(4分)腰长为5,高为4的等腰三角形的底边长为 .
三、解答题(15-18题每题10分,19题12分,共52分)
15.(10分)如图,在△ABC中,∠B=90°,AB=3,AC=5,D为BC边上的中点.
(1)求BD,AD的长度;
(2)将△ABC折叠,使A与D重合,得折痕EF交AB于点E,交AC于点F.求AE,BE的长度.
16.(10分)如图,AB为一棵大树(垂直于地面,即AB⊥BC),在树上距地面12m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处向上爬到树顶A处,再利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子经过的路程都是20m,求树高AB.
17.(10分)如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
①求证:EC=BD;
②若设△AEC三边分别为a、b、c,利用此图证明勾股定理.
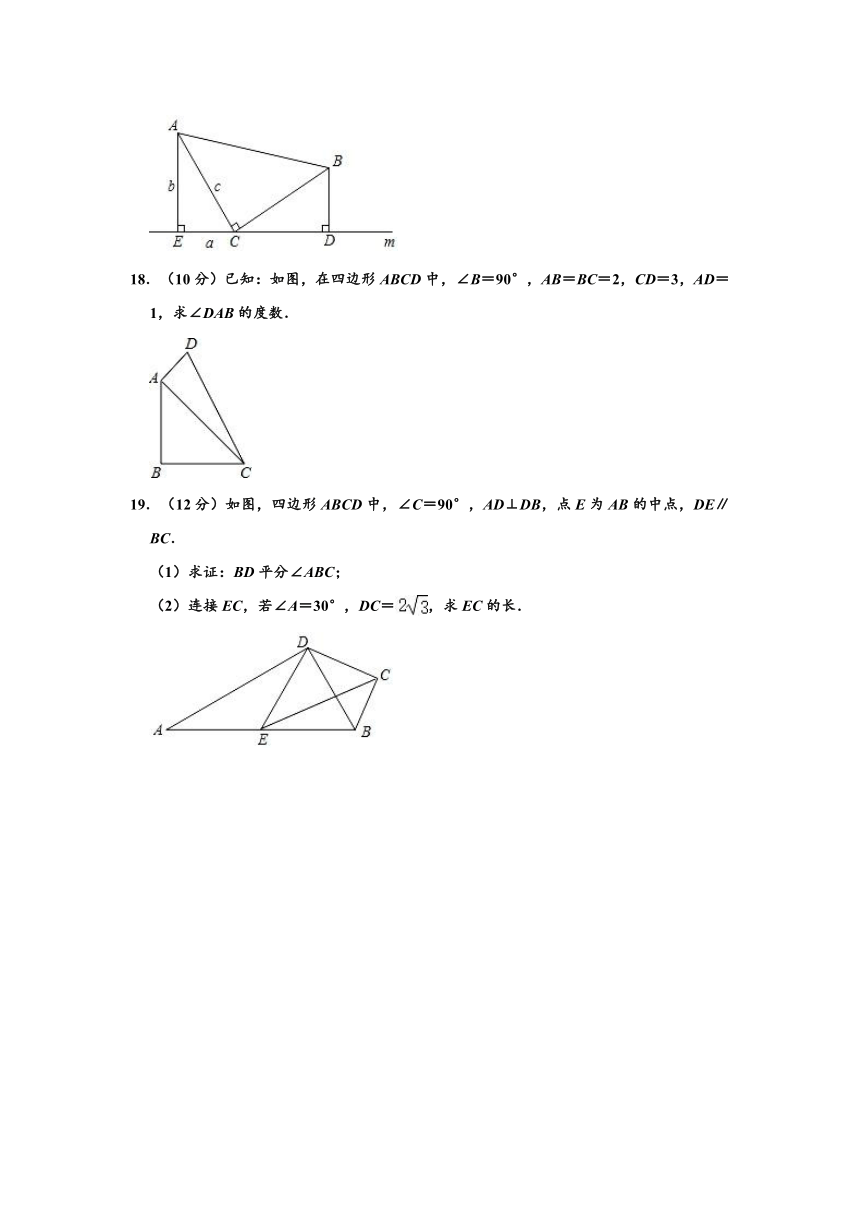
18.(10分)已知:如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,AD=1,求∠DAB的度数.
19.(12分)如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=,求EC的长.
参考答案
一、选择题(每小题3分,共24分)
1.(3分)勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A. B. C. D.
解:“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示:
故选:B.
2.(3分)如图中,边长k等于5的直角三角形有( )
A.1个 B.2个 C.3个 D.4个
解:如图1,k==5;
如图2,k==5;
如图3,k===8;
如图4,k===7.
故选:B.
3.(3分)五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
解:A、72+242=252,152+202≠242,222+202≠252,故A不正确;
B、72+242=252,152+202≠242,故B不正确;
C、72+242=252,152+202=252,故C正确;
D、72+202≠252,242+152≠252,故D不正确.
故选:C.
4.(3分)用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2﹣2ab+b2 D.c2=(a+b)2.
解:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,
里边的小四边形也为正方形,边长为b﹣a,
则有c2=ab×4+(b﹣a)2,
整理得:c2=a2+b2.
故选:A.
5.(3分)如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
解:过A作AE⊥BC,
∵AB=AC,
∴EC=BE=BC=4,
∴AE==3,
∵D是线段BC上的动点(不含端点B、C).
∴3≤AD<5,
∴AD=3或4,
∵线段AD长为正整数,
∴AD的可以有三条,长为4,3,4,
∴点D的个数共有3个,
故选:C.
6.(3分)如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了( )
A.2cm B.3cm C.4cm D.5cm
解:Rt△ACD中,AC=AB=4cm,CD=3cm;
根据勾股定理,得:AD==5cm;
∴AD+BD﹣AB=2AD﹣AB=10﹣8=2cm;
故橡皮筋被拉长了2cm.
故选:A.
7.(3分)如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.20 B.25 C.30 D.32
解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴BD=CD+BC=10+5=15,AD=20,
在直角三角形ABD中,根据勾股定理得:
∴AB==25;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴BD=CD+BC=20+5=25,AD=10,
在直角三角形ABD中,根据勾股定理得:
∴AB=;
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴AC=CD+AD=20+10=30,
在直角三角形ABC中,根据勾股定理得:
∴AB=;
∵25<5,
∴蚂蚁爬行的最短距离是25,
故选:B.
8.(3分)如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
解:由题可得,3=22﹣1,4=2×2,5=22+1,……
∴a=n2﹣1,b=2n,c=n2+1,
∴当c=n2+1=65时,n=8,
∴x=63,y=16,
∴x+y=79,
故选:C.
二、填空题(每小题4分;共24分)
9.(4分)直角三角形的两条直角边长分别为cm和cm,则这个直角三角形的周长为 (3+)cm .
解:∵直角三角形的两条直角边长分别为cm和cm,
∴直角三角形的斜边长为=2cm,
∴这个直角三角形的周长为+6=(3+)cm,
故答案为:(3+)cm.
10.(4分)如图所示的网格是正方形网格,△ABC和△CDE的顶点都是网格线交点,那么∠BAC+∠CDE= 45 °.
解:连接AD,
由勾股定理得:AD2=12+32=10,CD2=12+32=10,AC2=22+42=20,
∴AD=CD,AD2+CD2=AC2,
∴∠ADC=90°,
∴∠DAC=∠ACD=45°,
∵AB∥DE,
∴∠BAD+∠ADE=180°,
∴∠BAC+∠CDE=180°﹣90°﹣45°=45°,
故答案为:45°.
11.(4分)汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2:3,则中间围成的小正方形的面积与整个图形(大正方形)的面积之比为 1:13 .
解:设两直角边分别是2x,3x,则斜边即大正方形的边长为x,小正方形边长为x,
所以S大正方形=13x2,S小正方形=x2,S阴影=12x2,
∴中间围成的小正方形的面积与整个图形(大正方形)的面积之比为=1:13;
故答案为:1:13.
12.(4分)如图所示的网格是正方形网格,则∠PAB+∠PBA= 45 °(点A,B,P是网格线交点).
解:延长AP交格点于D,连接BD,
则PD2=BD2=1+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,
∴∠PDB=90°,
∴∠DPB=∠PAB+∠PBA=45°,
故答案为:45.
13.(4分)如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于 cm.
解:如图,折痕为GH,
由勾股定理得:AB==10cm,
由折叠得:AG=BG=AB=×10=5cm,GH⊥AB,
∴∠AGH=90°,
∵∠A=∠A,∠AGH=∠C=90°,
∴△ACB∽△AGH,
∴=,
∴=,
∴GH=cm.
故答案为:.
14.(4分)腰长为5,高为4的等腰三角形的底边长为 6或2或4 .
解:①如图1
当AB=AC=5,AD=4,
则BD=CD=3,
∴底边长为6;
②如图2.
当AB=AC=5,CD=4时,
则AD=3,
∴BD=2,
∴BC==2,
∴此时底边长为2;
③如图3:
当AB=AC=5,CD=4时,
则AD==3,
∴BD=8,
∴BC=4,
∴此时底边长为4.
故答案为:6或2或4.
三、解答题(15-18题每题10分,19题12分,共52分)
15.(10分)如图,在△ABC中,∠B=90°,AB=3,AC=5,D为BC边上的中点.
(1)求BD,AD的长度;
(2)将△ABC折叠,使A与D重合,得折痕EF交AB于点E,交AC于点F.求AE,BE的长度.
解:(1)∵∠B=90°,AB=3,AC=5,
∴BC===4,
∵D为BC边上的中点.
∴BD=CD=BC=2.
∴AD===;
(2)如图,连接DE,
∵将△ABC折叠,使A与D重合,得折痕EF交AB于点E,交AC于点F.
∴AE=DE,
在Rt△BDE中,BE2+BD2=DE2,
设BE=x,则AE=DE=3﹣x,
∴x2+22=(3﹣x)2,
解得x=,
∴AE=,BE=3﹣=.
16.(10分)如图,AB为一棵大树(垂直于地面,即AB⊥BC),在树上距地面12m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处向上爬到树顶A处,再利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子经过的路程都是20m,求树高AB.
解:设AD长为x m,则AC=(20﹣x) m,
BC=20﹣12=8(m),
在Rt△ABC中,由勾股定理得:
AB2+BC2=AC2,
则(12+x)2+82=(20﹣x)2,
解得:x=3,
故AB=AD+BD=3+12=15,
答:树的高度为15m.
17.(10分)如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
①求证:EC=BD;
②若设△AEC三边分别为a、b、c,利用此图证明勾股定理.
【解答】①证明:∵∠ACB=90°,
∴∠ACE+∠BCD=90°.
∵∠ACE+∠CAE=90°,
∴∠CAE=∠BCD.
在△AEC与△BCD中,
∴△CAE≌△BCD(AAS).
∴EC=BD;
②解:由①知:BD=CE=a
CD=AE=b
∴S梯形AEDB=(a+b)(a+b)
=a2+ab+b2.
又∵S梯形AEDB=S△AEC+S△BCD+S△ABC
=ab+ab+c2
=ab+c2.
∴a2+ab+b2=ab+c2.
整理,得a2+b2=c2.
18.(10分)已知:如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,AD=1,求∠DAB的度数.
解:∵∠B=90°,AB=BC=2,
∴AC==2,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠DAB=45°+90°=135°.
故∠DAB的度数为135°.
19.(12分)如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=,求EC的长.
【解答】(1)证明:∵AD⊥DB,点E为AB的中点,
∴DE=BE=AB.
∴∠1=∠2.
∵DE∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴BD平分∠ABC.
(2)解:∵AD⊥DB,∠A=30°
∴∠1=60°.
∴∠3=∠2=60°.
∵∠BCD=90°,
∴∠4=30°.
∴∠CDE=∠2+∠4=90°.
在Rt△BCD中,∠3=60°,DC=2,
∴DB=4.
∵DE=BE,∠1=60°,
∴DE=DB=4.
∴EC===2.
一、选择题(共8小题).
1.(3分)勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A. B. C. D.
2.(3分)如图中,边长k等于5的直角三角形有( )
A.1个 B.2个 C.3个 D.4个
3.(3分)五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
4.(3分)用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2﹣2ab+b2 D.c2=(a+b)2.
5.(3分)如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
6.(3分)如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了( )
A.2cm B.3cm C.4cm D.5cm
7.(3分)如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.20 B.25 C.30 D.32
8.(3分)如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
二、填空题(每小题4分;共24分)
9.(4分)直角三角形的两条直角边长分别为cm和cm,则这个直角三角形的周长为 .
10.(4分)如图所示的网格是正方形网格,△ABC和△CDE的顶点都是网格线交点,那么∠BAC+∠CDE= °.
11.(4分)汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2:3,则中间围成的小正方形的面积与整个图形(大正方形)的面积之比为 .
12.(4分)如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
13.(4分)如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于 cm.
14.(4分)腰长为5,高为4的等腰三角形的底边长为 .
三、解答题(15-18题每题10分,19题12分,共52分)
15.(10分)如图,在△ABC中,∠B=90°,AB=3,AC=5,D为BC边上的中点.
(1)求BD,AD的长度;
(2)将△ABC折叠,使A与D重合,得折痕EF交AB于点E,交AC于点F.求AE,BE的长度.
16.(10分)如图,AB为一棵大树(垂直于地面,即AB⊥BC),在树上距地面12m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处向上爬到树顶A处,再利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子经过的路程都是20m,求树高AB.
17.(10分)如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
①求证:EC=BD;
②若设△AEC三边分别为a、b、c,利用此图证明勾股定理.
18.(10分)已知:如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,AD=1,求∠DAB的度数.
19.(12分)如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=,求EC的长.
参考答案
一、选择题(每小题3分,共24分)
1.(3分)勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A. B. C. D.
解:“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示:
故选:B.
2.(3分)如图中,边长k等于5的直角三角形有( )
A.1个 B.2个 C.3个 D.4个
解:如图1,k==5;
如图2,k==5;
如图3,k===8;
如图4,k===7.
故选:B.
3.(3分)五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
解:A、72+242=252,152+202≠242,222+202≠252,故A不正确;
B、72+242=252,152+202≠242,故B不正确;
C、72+242=252,152+202=252,故C正确;
D、72+202≠252,242+152≠252,故D不正确.
故选:C.
4.(3分)用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2﹣2ab+b2 D.c2=(a+b)2.
解:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,
里边的小四边形也为正方形,边长为b﹣a,
则有c2=ab×4+(b﹣a)2,
整理得:c2=a2+b2.
故选:A.
5.(3分)如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
解:过A作AE⊥BC,
∵AB=AC,
∴EC=BE=BC=4,
∴AE==3,
∵D是线段BC上的动点(不含端点B、C).
∴3≤AD<5,
∴AD=3或4,
∵线段AD长为正整数,
∴AD的可以有三条,长为4,3,4,
∴点D的个数共有3个,
故选:C.
6.(3分)如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了( )
A.2cm B.3cm C.4cm D.5cm
解:Rt△ACD中,AC=AB=4cm,CD=3cm;
根据勾股定理,得:AD==5cm;
∴AD+BD﹣AB=2AD﹣AB=10﹣8=2cm;
故橡皮筋被拉长了2cm.
故选:A.
7.(3分)如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.20 B.25 C.30 D.32
解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴BD=CD+BC=10+5=15,AD=20,
在直角三角形ABD中,根据勾股定理得:
∴AB==25;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴BD=CD+BC=20+5=25,AD=10,
在直角三角形ABD中,根据勾股定理得:
∴AB=;
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴AC=CD+AD=20+10=30,
在直角三角形ABC中,根据勾股定理得:
∴AB=;
∵25<5,
∴蚂蚁爬行的最短距离是25,
故选:B.
8.(3分)如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
解:由题可得,3=22﹣1,4=2×2,5=22+1,……
∴a=n2﹣1,b=2n,c=n2+1,
∴当c=n2+1=65时,n=8,
∴x=63,y=16,
∴x+y=79,
故选:C.
二、填空题(每小题4分;共24分)
9.(4分)直角三角形的两条直角边长分别为cm和cm,则这个直角三角形的周长为 (3+)cm .
解:∵直角三角形的两条直角边长分别为cm和cm,
∴直角三角形的斜边长为=2cm,
∴这个直角三角形的周长为+6=(3+)cm,
故答案为:(3+)cm.
10.(4分)如图所示的网格是正方形网格,△ABC和△CDE的顶点都是网格线交点,那么∠BAC+∠CDE= 45 °.
解:连接AD,
由勾股定理得:AD2=12+32=10,CD2=12+32=10,AC2=22+42=20,
∴AD=CD,AD2+CD2=AC2,
∴∠ADC=90°,
∴∠DAC=∠ACD=45°,
∵AB∥DE,
∴∠BAD+∠ADE=180°,
∴∠BAC+∠CDE=180°﹣90°﹣45°=45°,
故答案为:45°.
11.(4分)汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2:3,则中间围成的小正方形的面积与整个图形(大正方形)的面积之比为 1:13 .
解:设两直角边分别是2x,3x,则斜边即大正方形的边长为x,小正方形边长为x,
所以S大正方形=13x2,S小正方形=x2,S阴影=12x2,
∴中间围成的小正方形的面积与整个图形(大正方形)的面积之比为=1:13;
故答案为:1:13.
12.(4分)如图所示的网格是正方形网格,则∠PAB+∠PBA= 45 °(点A,B,P是网格线交点).
解:延长AP交格点于D,连接BD,
则PD2=BD2=1+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,
∴∠PDB=90°,
∴∠DPB=∠PAB+∠PBA=45°,
故答案为:45.
13.(4分)如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于 cm.
解:如图,折痕为GH,
由勾股定理得:AB==10cm,
由折叠得:AG=BG=AB=×10=5cm,GH⊥AB,
∴∠AGH=90°,
∵∠A=∠A,∠AGH=∠C=90°,
∴△ACB∽△AGH,
∴=,
∴=,
∴GH=cm.
故答案为:.
14.(4分)腰长为5,高为4的等腰三角形的底边长为 6或2或4 .
解:①如图1
当AB=AC=5,AD=4,
则BD=CD=3,
∴底边长为6;
②如图2.
当AB=AC=5,CD=4时,
则AD=3,
∴BD=2,
∴BC==2,
∴此时底边长为2;
③如图3:
当AB=AC=5,CD=4时,
则AD==3,
∴BD=8,
∴BC=4,
∴此时底边长为4.
故答案为:6或2或4.
三、解答题(15-18题每题10分,19题12分,共52分)
15.(10分)如图,在△ABC中,∠B=90°,AB=3,AC=5,D为BC边上的中点.
(1)求BD,AD的长度;
(2)将△ABC折叠,使A与D重合,得折痕EF交AB于点E,交AC于点F.求AE,BE的长度.
解:(1)∵∠B=90°,AB=3,AC=5,
∴BC===4,
∵D为BC边上的中点.
∴BD=CD=BC=2.
∴AD===;
(2)如图,连接DE,
∵将△ABC折叠,使A与D重合,得折痕EF交AB于点E,交AC于点F.
∴AE=DE,
在Rt△BDE中,BE2+BD2=DE2,
设BE=x,则AE=DE=3﹣x,
∴x2+22=(3﹣x)2,
解得x=,
∴AE=,BE=3﹣=.
16.(10分)如图,AB为一棵大树(垂直于地面,即AB⊥BC),在树上距地面12m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处向上爬到树顶A处,再利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子经过的路程都是20m,求树高AB.
解:设AD长为x m,则AC=(20﹣x) m,
BC=20﹣12=8(m),
在Rt△ABC中,由勾股定理得:
AB2+BC2=AC2,
则(12+x)2+82=(20﹣x)2,
解得:x=3,
故AB=AD+BD=3+12=15,
答:树的高度为15m.
17.(10分)如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
①求证:EC=BD;
②若设△AEC三边分别为a、b、c,利用此图证明勾股定理.
【解答】①证明:∵∠ACB=90°,
∴∠ACE+∠BCD=90°.
∵∠ACE+∠CAE=90°,
∴∠CAE=∠BCD.
在△AEC与△BCD中,
∴△CAE≌△BCD(AAS).
∴EC=BD;
②解:由①知:BD=CE=a
CD=AE=b
∴S梯形AEDB=(a+b)(a+b)
=a2+ab+b2.
又∵S梯形AEDB=S△AEC+S△BCD+S△ABC
=ab+ab+c2
=ab+c2.
∴a2+ab+b2=ab+c2.
整理,得a2+b2=c2.
18.(10分)已知:如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,AD=1,求∠DAB的度数.
解:∵∠B=90°,AB=BC=2,
∴AC==2,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠DAB=45°+90°=135°.
故∠DAB的度数为135°.
19.(12分)如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=,求EC的长.
【解答】(1)证明:∵AD⊥DB,点E为AB的中点,
∴DE=BE=AB.
∴∠1=∠2.
∵DE∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴BD平分∠ABC.
(2)解:∵AD⊥DB,∠A=30°
∴∠1=60°.
∴∠3=∠2=60°.
∵∠BCD=90°,
∴∠4=30°.
∴∠CDE=∠2+∠4=90°.
在Rt△BCD中,∠3=60°,DC=2,
∴DB=4.
∵DE=BE,∠1=60°,
∴DE=DB=4.
∴EC===2.
