第三章 万有引力定律 本章小结课件 28张PPT
文档属性
| 名称 | 第三章 万有引力定律 本章小结课件 28张PPT |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-25 00:00:00 | ||
图片预览




文档简介
第
4
节
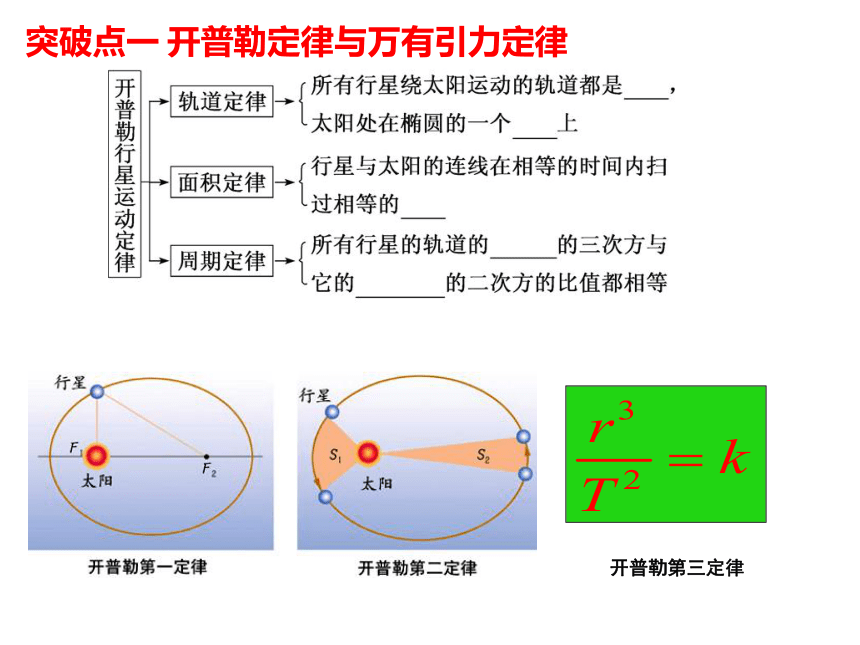
开普勒第三定律
突破点一 开普勒定律与万有引力定律
1.万有引力定律的发现实现了物理学史上的第一次大统一——“地上力学”和“天上力学”的统一。它表明天体运动和地面上物体的运动遵循相同规律。牛顿在发现万有引力定律的过程中将行星的椭圆轨道运动假想成圆周运动;另外,还应用到了其它的规律和结论,其中有 ( )
(A)牛顿第二定律
(B)牛顿第三定律
(C)开普勒的研究成果
(D)卡文迪许通过扭秤实验得出的引力常数
而
带入上式
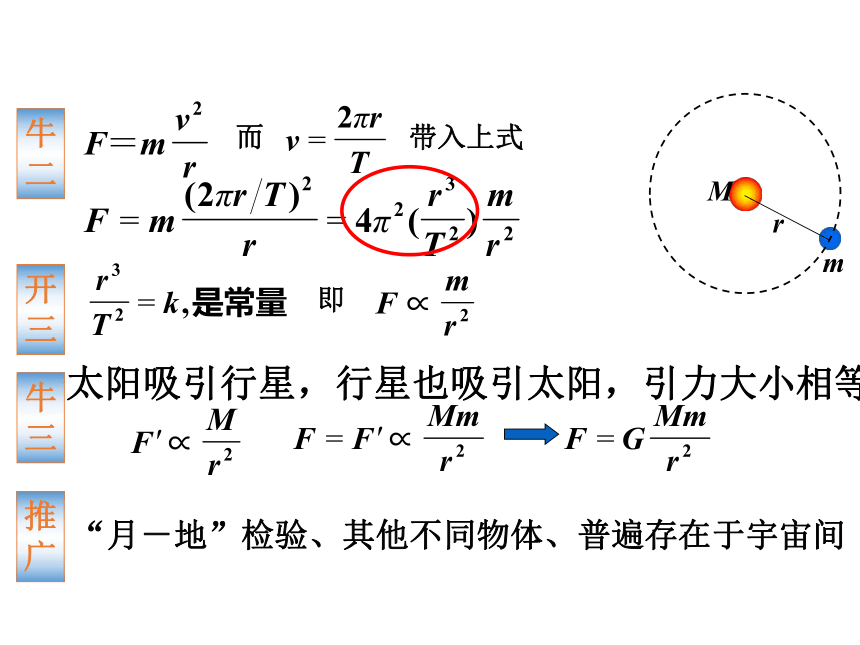
牛二
开三
牛三
即
r
m
M
推广
太阳吸引行星,行星也吸引太阳,引力大小相等
“月-地”检验、其他不同物体、普遍存在于宇宙间
卡文迪许扭称实验(1789年)-----放大法
两次放大及等效的思想 :
(1)扭秤装置把微小力转变成力矩来反映
(2)扭转角度(微小形变)通过光标的移动来反映
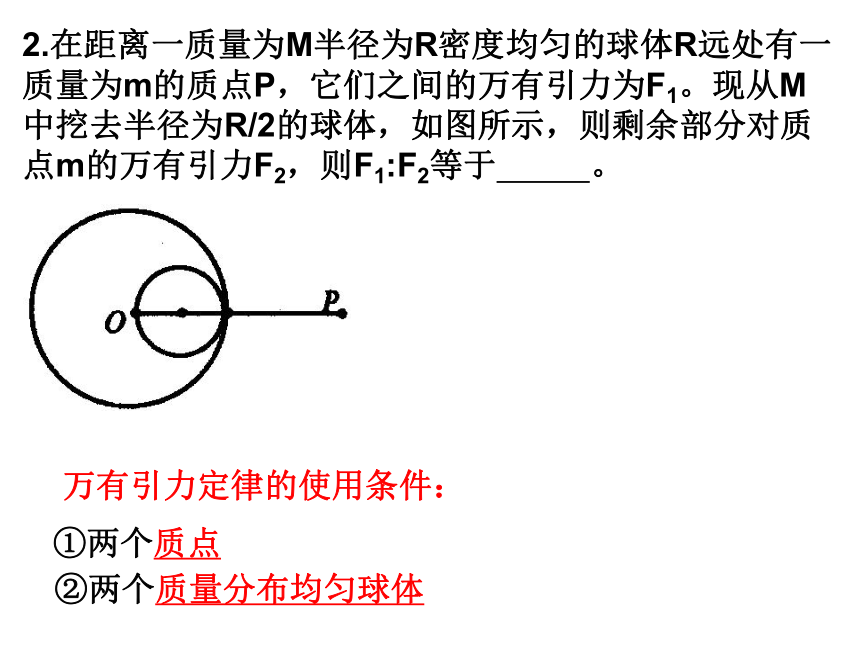
2.在距离一质量为M半径为R密度均匀的球体R远处有一质量为m的质点P,它们之间的万有引力为F1。现从M中挖去半径为R/2的球体,如图所示,则剩余部分对质点m的万有引力F2,则F1:F2等于 。
万有引力定律的使用条件:
①两个质点
②两个质量分布均匀球体
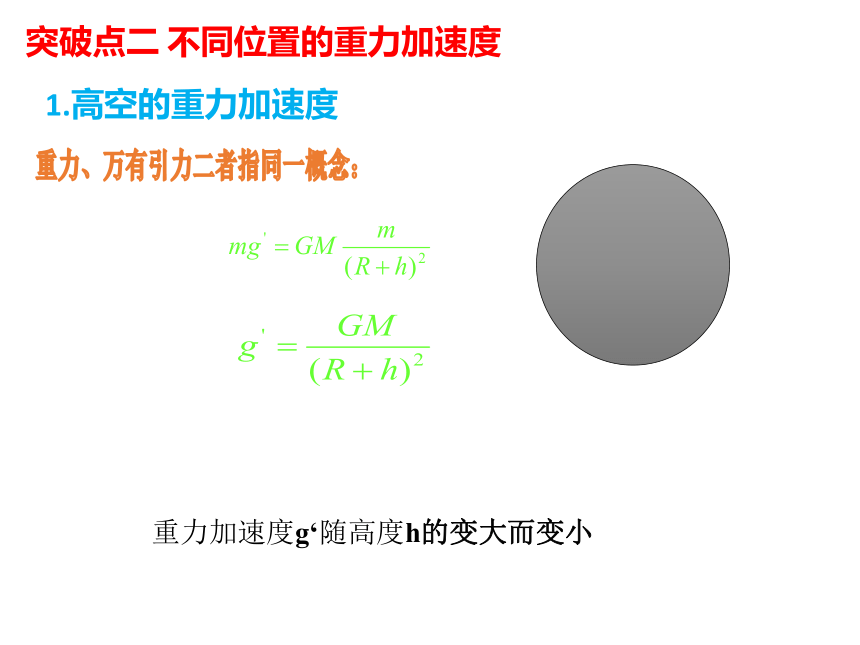
重力、万有引力二者指同一概念:
重力加速度g‘随高度h的变大而变小
突破点二 不同位置的重力加速度
1.高空的重力加速度
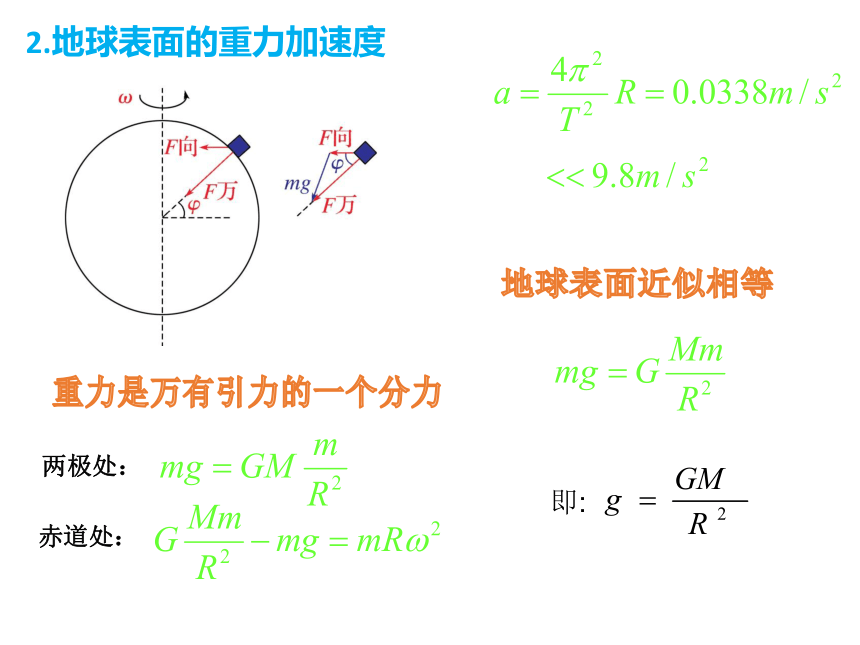
重力是万有引力的一个分力
2.地球表面的重力加速度
两极处:
赤道处:
地球表面近似相等
即:
3.地球表面以下的重力加速度
3.(2012 大纲卷)一单摆在地面处的摆动周期与在某矿井底部摆动周期的比值为k。设地球的半径为R。假定地球的密度均匀。已知质量均匀分布的球壳对壳内物体的引力为零,求矿井的深度d。
4.假设地球是一半径为R,质量分布均匀的球体。已知质量分布均匀的球壳对壳内物体引力为零,地球表面处引力加速度为g。则关于地球引力加速度a随地球球心到某点距离r的变化图像正确的是(?????)
B
5.假设地球是一半径为R、质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。矿井底部和地面处的重力加速度大小之比为
A.?? B.? ??? C.???? D.?
A
6.目前,我国探月工程已取得重大进展.在不久的将来,我国宇航员将登上月球.
假如给你提供三组信息:
①一同学在家中用长为L的细线和一个小螺丝帽组成了一个单摆,测得该单摆的振动周期为T;
②一宇航员在月球表面上以初速度v0竖直上抛一小球,经过时间t,小球落回原处;
③地球的质量约为月球质量的81倍,地球半径为R.请你根据上述信息求:
(1)地球表面的重力加速度;
(2)月球表面的重力加速度;
(3)月球的半径.
方法一 :测“g”法( 重力近似等于万有引力)
基本思路:
“黄金”代换公式!
突破点三 中心天体质量和密度的计算
方法二:环绕法 (万有引力充当向心力)
基本思路:
中心天体
环绕天体
M
r
m
能计算月球的质量吗?
只能计算中心天体的质量
不能计算环绕天体的质量
若T是近地卫星的周期,则r≈R
M
V
r
=
若地球的半径为R=6.4 × 106m,能否算出地球的密度呢?
计算天体密度
M
V
r
=
计算天体密度
开放题:已知地球半径、月地距离、地球表面加速度、月球周期、同步卫星周期、同步卫星距离等,可以有哪些求地球质量的方法?
7、《教材》P51 发展空间
估测太阳的密度
所测的物理量:
测量原理:
测量说明:
1、观测时间:
先测质量、再测D和d
地球的公转周期T和测D和d
早晨或傍晚或有保护眼睛的工具
2、测D和d:
小孔成像法
?
B
9.假设地球可视为质量均匀分布的球体.已知地球表面重力加速度在两极的大小为g0,在赤道的大小为g,地球自转的周期为T,引力常量为G.地球的密度为( )
B
小结:
1.天体表面及其某一高度处的重力加速度的求法
2.地球表面的物体运动规律的迁移应用
在地球上所有只在重力作用下的运动形式,如自由落体运动、竖直上抛运动、平抛运动、斜抛运动等,其运动规律和研究方法同样适用于在其他星球表面的同类运动的分析,只是当地重力加速度取值不同而已.
天体质量和密度的计算
②万有引力提供天体运动的向心力
R:中心天体半径
T:环绕天体公转周期
r:环绕天体公转半径
R:天体半径
g:天体表面重力加速度
①忽略天体自转影响,物体在天体表面的重力等于引力
注意:能测量的仅是中心天体的质量和密度
4
节
开普勒第三定律
突破点一 开普勒定律与万有引力定律
1.万有引力定律的发现实现了物理学史上的第一次大统一——“地上力学”和“天上力学”的统一。它表明天体运动和地面上物体的运动遵循相同规律。牛顿在发现万有引力定律的过程中将行星的椭圆轨道运动假想成圆周运动;另外,还应用到了其它的规律和结论,其中有 ( )
(A)牛顿第二定律
(B)牛顿第三定律
(C)开普勒的研究成果
(D)卡文迪许通过扭秤实验得出的引力常数
而
带入上式
牛二
开三
牛三
即
r
m
M
推广
太阳吸引行星,行星也吸引太阳,引力大小相等
“月-地”检验、其他不同物体、普遍存在于宇宙间
卡文迪许扭称实验(1789年)-----放大法
两次放大及等效的思想 :
(1)扭秤装置把微小力转变成力矩来反映
(2)扭转角度(微小形变)通过光标的移动来反映
2.在距离一质量为M半径为R密度均匀的球体R远处有一质量为m的质点P,它们之间的万有引力为F1。现从M中挖去半径为R/2的球体,如图所示,则剩余部分对质点m的万有引力F2,则F1:F2等于 。
万有引力定律的使用条件:
①两个质点
②两个质量分布均匀球体
重力、万有引力二者指同一概念:
重力加速度g‘随高度h的变大而变小
突破点二 不同位置的重力加速度
1.高空的重力加速度
重力是万有引力的一个分力
2.地球表面的重力加速度
两极处:
赤道处:
地球表面近似相等
即:
3.地球表面以下的重力加速度
3.(2012 大纲卷)一单摆在地面处的摆动周期与在某矿井底部摆动周期的比值为k。设地球的半径为R。假定地球的密度均匀。已知质量均匀分布的球壳对壳内物体的引力为零,求矿井的深度d。
4.假设地球是一半径为R,质量分布均匀的球体。已知质量分布均匀的球壳对壳内物体引力为零,地球表面处引力加速度为g。则关于地球引力加速度a随地球球心到某点距离r的变化图像正确的是(?????)
B
5.假设地球是一半径为R、质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。矿井底部和地面处的重力加速度大小之比为
A.?? B.? ??? C.???? D.?
A
6.目前,我国探月工程已取得重大进展.在不久的将来,我国宇航员将登上月球.
假如给你提供三组信息:
①一同学在家中用长为L的细线和一个小螺丝帽组成了一个单摆,测得该单摆的振动周期为T;
②一宇航员在月球表面上以初速度v0竖直上抛一小球,经过时间t,小球落回原处;
③地球的质量约为月球质量的81倍,地球半径为R.请你根据上述信息求:
(1)地球表面的重力加速度;
(2)月球表面的重力加速度;
(3)月球的半径.
方法一 :测“g”法( 重力近似等于万有引力)
基本思路:
“黄金”代换公式!
突破点三 中心天体质量和密度的计算
方法二:环绕法 (万有引力充当向心力)
基本思路:
中心天体
环绕天体
M
r
m
能计算月球的质量吗?
只能计算中心天体的质量
不能计算环绕天体的质量
若T是近地卫星的周期,则r≈R
M
V
r
=
若地球的半径为R=6.4 × 106m,能否算出地球的密度呢?
计算天体密度
M
V
r
=
计算天体密度
开放题:已知地球半径、月地距离、地球表面加速度、月球周期、同步卫星周期、同步卫星距离等,可以有哪些求地球质量的方法?
7、《教材》P51 发展空间
估测太阳的密度
所测的物理量:
测量原理:
测量说明:
1、观测时间:
先测质量、再测D和d
地球的公转周期T和测D和d
早晨或傍晚或有保护眼睛的工具
2、测D和d:
小孔成像法
?
B
9.假设地球可视为质量均匀分布的球体.已知地球表面重力加速度在两极的大小为g0,在赤道的大小为g,地球自转的周期为T,引力常量为G.地球的密度为( )
B
小结:
1.天体表面及其某一高度处的重力加速度的求法
2.地球表面的物体运动规律的迁移应用
在地球上所有只在重力作用下的运动形式,如自由落体运动、竖直上抛运动、平抛运动、斜抛运动等,其运动规律和研究方法同样适用于在其他星球表面的同类运动的分析,只是当地重力加速度取值不同而已.
天体质量和密度的计算
②万有引力提供天体运动的向心力
R:中心天体半径
T:环绕天体公转周期
r:环绕天体公转半径
R:天体半径
g:天体表面重力加速度
①忽略天体自转影响,物体在天体表面的重力等于引力
注意:能测量的仅是中心天体的质量和密度
