4.5 机械能守恒定律课件 30张PPT
图片预览




文档简介
4.5 机械能守恒定律
2、动能定理的内容是什么?
3、重力做功与重力势能的关系是什么?
1、本章学了哪几种能,如何定义,大小如
何计算?
知识回顾
重力势能
弹性势能
势能
动能
机械能
机械能的概念:
物体在某状态时的动能、重力势能和弹性势能的总和叫做物体的机械能。
符号:E=EK+EP
一、机械能
观察与思考:
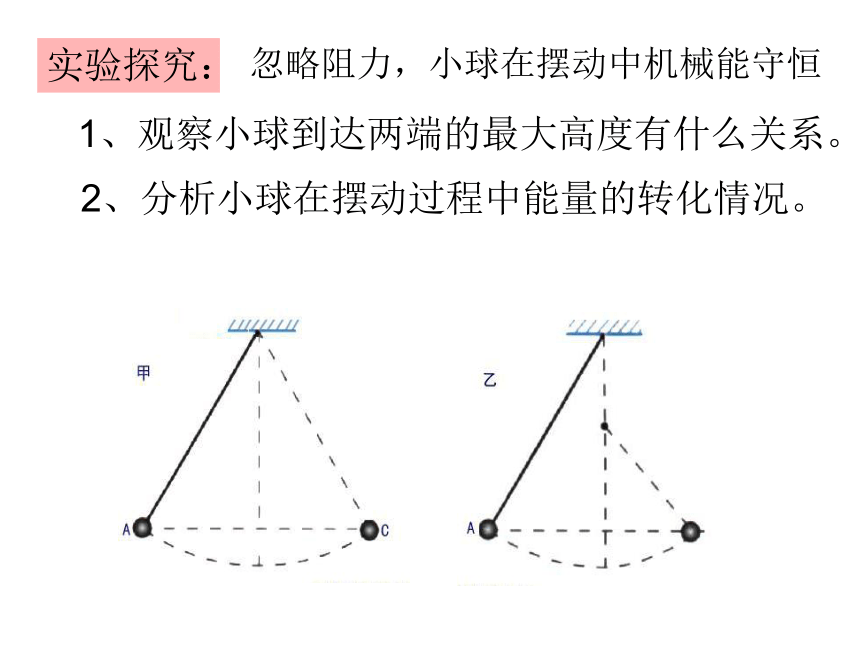
实验探究:
忽略阻力,小球在摆动中机械能守恒
1、观察小球到达两端的最大高度有什么关系。
2、分析小球在摆动过程中能量的转化情况。
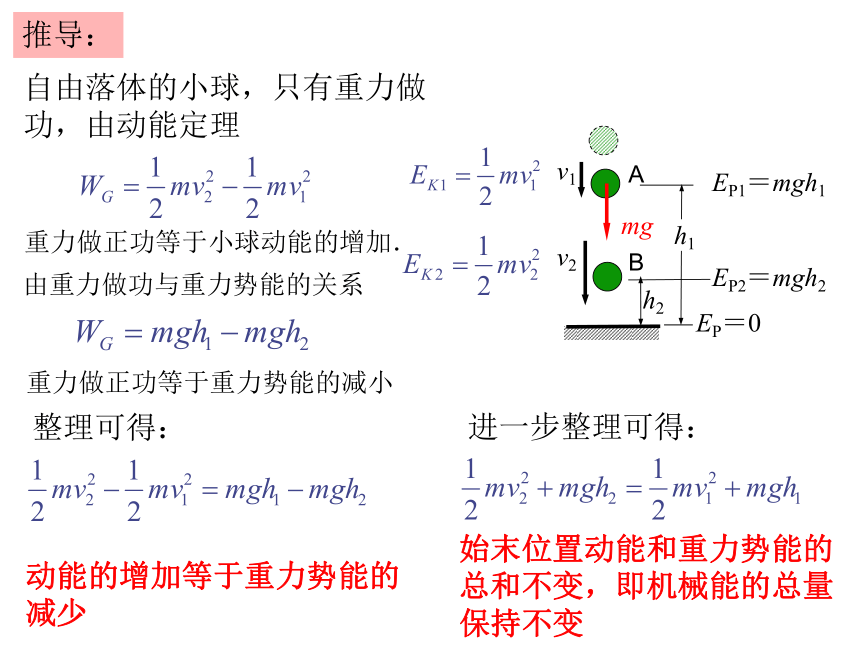
推导:
重力做正功等于重力势能的减小
EP2=mgh2
EP1=mgh1
自由落体的小球,只有重力做功,由动能定理
重力做正功等于小球动能的增加.
由重力做功与重力势能的关系
整理可得:
动能的增加等于重力势能的减少
进一步整理可得:
始末位置动能和重力势能的总和不变,即机械能的总量保持不变
EP=0
v2
h1
v1
h2
mg
A
B
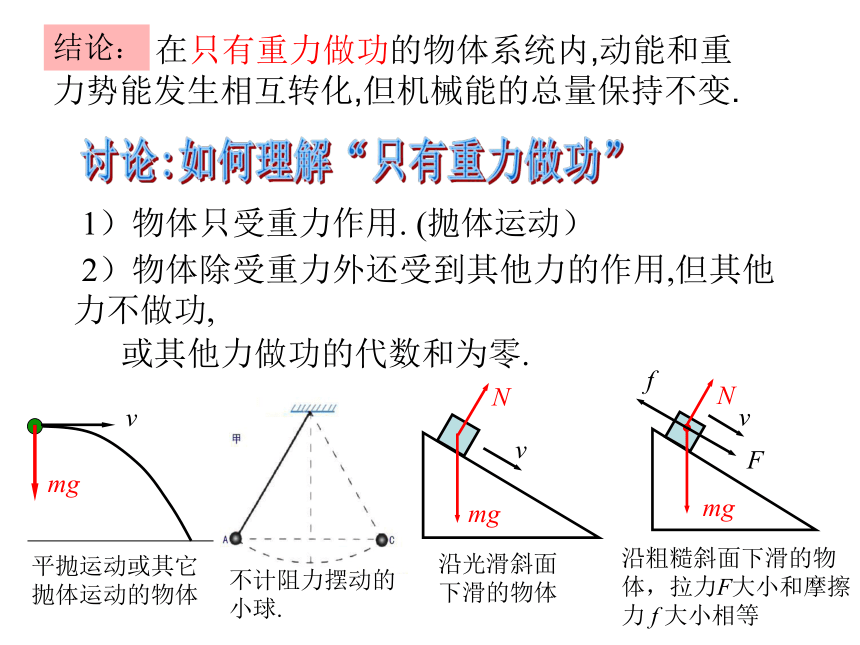
在只有重力做功的物体系统内,动能和重力势能发生相互转化,但机械能的总量保持不变.
平抛运动或其它抛体运动的物体
mg
v
沿光滑斜面下滑的物体
v
mg
N
沿粗糙斜面下滑的物体,拉力F大小和摩擦力 f 大小相等
v
mg
N
F
f
结论:
1)物体只受重力作用. (抛体运动)
2)物体除受重力外还受到其他力的作用,但其他力不做功,
或其他力做功的代数和为零.
不计阻力摆动的小球.
H
h
质量为m的小球,从离地面高H处自由下落到一轻弹簧上,弹簧长为L,弹簧压缩到最短时小球离地面高为h,忽略空气阻力,求:弹簧的最大弹性势能
弹簧最短时,弹性势能最大.只有重力和弹簧弹力做功,小球和弹簧系统机械能守恒.在最高点和最低点小球的动能为零,减少的重力势能等于增加的弹性势能.
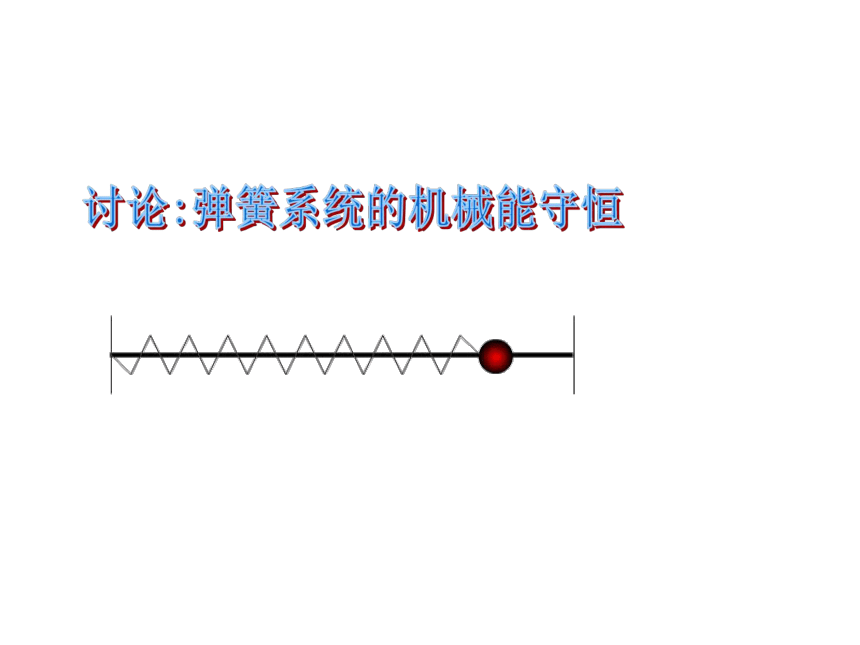
竖直方向的弹簧振子,系统的机械能守恒吗?
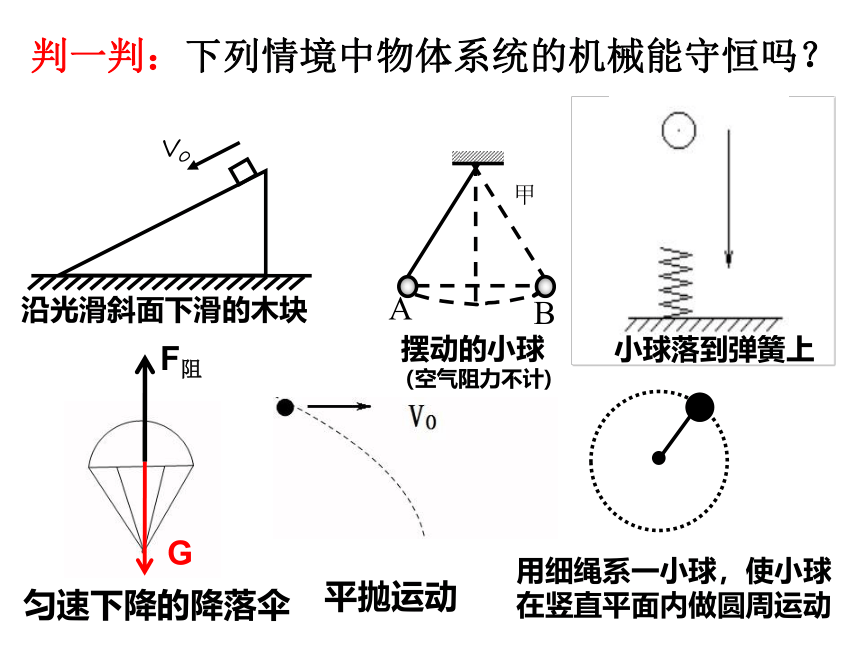
判一判:下列情境中物体系统的机械能守恒吗?
乙
甲
A
B
C
A
沿光滑斜面下滑的木块
V0
F阻
G
匀速下降的降落伞
平抛运动
用细绳系一小球,使小球在竖直平面内做圆周运动
摆动的小球
(空气阻力不计)
小球落到弹簧上
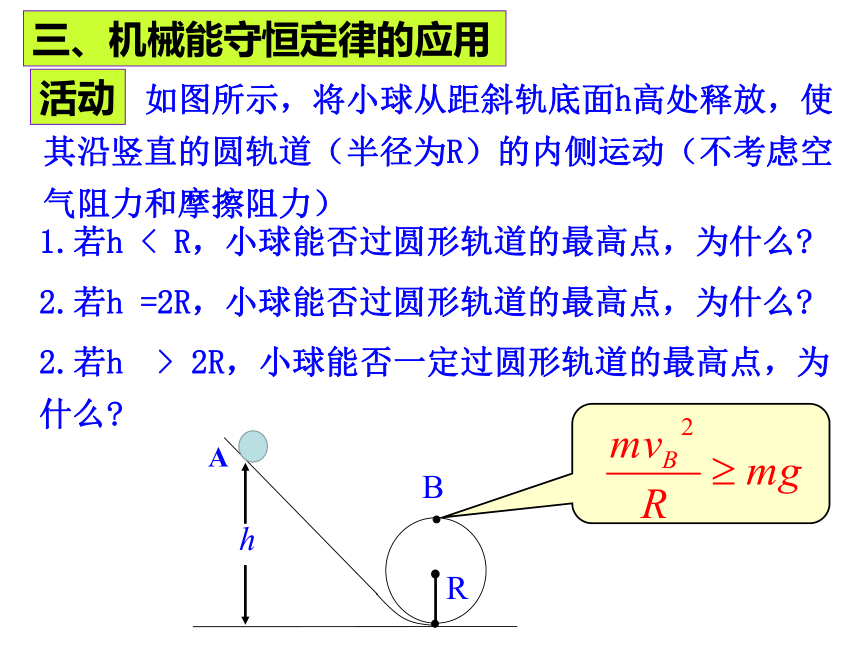
如图所示,将小球从距斜轨底面h高处释放,使其沿竖直的圆轨道(半径为R)的内侧运动(不考虑空气阻力和摩擦阻力)
h
B
A
R
三、机械能守恒定律的应用
活动
1.若h < R,小球能否过圆形轨道的最高点,为什么?
2.若h =2R,小球能否过圆形轨道的最高点,为什么?
2.若h > 2R,小球能否一定过圆形轨道的最高点,为什么?
巩固练习:
1.关于机械能是否守恒,下列说法正确的是 ( )
A.做匀速直线运动的物体机械能一定守恒
B.做圆周运动的物体机械能一定守恒
C.做变速运动的物体机械能可能守恒
D.合外力对物体做功为零,机械能一定守恒
C
2.如图所示,木块均在固定的斜面上运动,其中图A、B、C中的斜面是光滑的,图D中的斜面是粗糙的,图A、B中的F为木块所受的外力,方向如图中箭头所示,图A、B、D中的木块向下运动,图C中的木块向上运动.在这四个图所示的运动过程中机械能守恒的是 ( )
C
3、质量分别为m和2m的两个小球A和B,中间用轻质杆相连,在杆的中点O处有一固定转动轴,把杆置于水平位置后释放,在B球顺时针摆动到最低位置的过程中 ( )
A.A球的重力势能增加,动能也增加,A球和地球组成的系统机械能不守恒
B.B球的重力势能减少,动能增加,B球和地球组成的系统机械能守恒
C.A球、B球和地球组成的系统机械能守恒
D.A球、B球和地球组成的系统机械不守恒
AC
4、光滑圆管形轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r< (1)若要小球能从C端出来,初速度v0多大?
(2)在小球从C端出来的瞬间,对管壁压力有哪几种典型情况,初速度v0各应满足什么条件?
v0>
刚好对管壁无压力
v0=
对下管壁有压力
对上管壁有压力
v0>
5、用细绳悬挂一个质量为m的小球,悬点为O点,把小球拉至A点,使悬线与水平方向成30°角,由静止释放小球,问:小球运动到悬点的正下方B点时,细绳受到的拉力?
A
O
C
B
3.5mg
注意C点速度的突变,突变前后机械能不守恒
6、如图所示,小球A用不可伸长的轻绳悬于O点,在O点的正下方有一固定的钉子,OB=y.初始时,小球A与O同水平面,无初速释放A,绳长为L,且绳上最大拉力为11mg.为使球能绕B点做圆周运动且绳不断,求y的取值范围.
C点无速度的突变,机械能守恒
7、在高1.5 m的光滑平台上有一个质量为2 kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g取10 m/s2)( )
A.10 J
B.15 J
C.20 J
D.25 J
A
8、如图所示,一个质量m=0.2kg的光滑小球系于轻质弹簧的一端,且套在竖立的圆环上,弹簧的上端固定于环的最高点A,环的半径R=0.50m。弹簧的原长l0=0.5m,劲度系数为k=4.8N/m。若小球从图示位置B点由静止开始滑动到最低点C时,弹簧的弹性势能EP弹=0.6J,求:
(1)小球到C点时速度的大小;
(2)小球在C点对环的作用力.(g取10m/s2)
3m/s;3.2N,方向向下
9、一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )
A.杆转到竖直位置时,A、B两球的速度大小相等为
B.杆转到竖直位置时,杆对B球的作用力向上,
大小为(1/3)mg
C.杆转到竖直位置时,B球的机械能减少了(4/3)mgL
D.由于忽略一切摩擦阻力,A球机械能一定守恒
B
二、研究对象为两个物体
10、一轻质杆上有两个质量相等的小球A、B,轻杆可绕O点在竖直平面内自由转动.OA=OB=l,先将杆拉至水平面后由静止释放,则当轻杆转到竖直方向时,A、B两球的速度大小分别为多少?
三、验证机械能守恒定律实验
1.实验过程
(1)实验步骤
①安装:将打点计时器固定在铁架台上;用导线将打点计时器与低压交流电源相连接.
②接电源,打纸带:把纸带的一端在重物上用夹子固定好,另一端穿过打点计时器的限位孔,用手提着纸带使重物停靠在打点计时器附近,接通电源,待打点稳定后松开纸带,让重物自由下落.重复几次,打下3~5条纸带.
③选纸带:选取点迹较为清晰的.挑选纸带上第一个点及距离第一个点较远的点,并依次标上0,1,2,3,….
④数据测量:测出0到点1、点2、点3……的距离,即为对应的下落高度h1、h2、h3….
(2)数据处理
3.误差分析
(1)本实验的误差主要是由于纸带测量产生的偶然误差和重物、纸带运动中空气阻力及纸带与打点计时器摩擦阻力引起的系统误差,使动能的增加量稍小于势能的减少量.
(2)测量时采取多次测量求平均值来减小偶然误差,安装打点计时器时使两限位孔中线竖直,并且选择质量适当大些,体积尽量小些的重物来减小系统误差.
(3)打点计时器周期变化带来误差.
计算物体的速度,可有三种方法
第1种方法是根据机械能守恒定律得到的,而我们的目的就是验证机械能守恒定律,所以不能用
第2种方法认为加速度为g,由于各种摩擦阻力不可避免,所以实际加速度必将小于g,这样将得到机械能增加的结论,有阻力作用机械能应该是减少的,故这种方法也不能用
即时应用(即时突破,小试牛刀)
如图4-5-7是用自由落体法验证机械能守恒定律时得到的一条纸带.有关尺寸在图中已注明.我们选中n点来验证机械能守恒定律.下面举出了一些计算n点速度的方法,其中正确的是( )
图4-5-7
解析:选CD.vn应表示从(n-1)到(n+1)间的平均速度.C、D对,A、B错.
2、动能定理的内容是什么?
3、重力做功与重力势能的关系是什么?
1、本章学了哪几种能,如何定义,大小如
何计算?
知识回顾
重力势能
弹性势能
势能
动能
机械能
机械能的概念:
物体在某状态时的动能、重力势能和弹性势能的总和叫做物体的机械能。
符号:E=EK+EP
一、机械能
观察与思考:
实验探究:
忽略阻力,小球在摆动中机械能守恒
1、观察小球到达两端的最大高度有什么关系。
2、分析小球在摆动过程中能量的转化情况。
推导:
重力做正功等于重力势能的减小
EP2=mgh2
EP1=mgh1
自由落体的小球,只有重力做功,由动能定理
重力做正功等于小球动能的增加.
由重力做功与重力势能的关系
整理可得:
动能的增加等于重力势能的减少
进一步整理可得:
始末位置动能和重力势能的总和不变,即机械能的总量保持不变
EP=0
v2
h1
v1
h2
mg
A
B
在只有重力做功的物体系统内,动能和重力势能发生相互转化,但机械能的总量保持不变.
平抛运动或其它抛体运动的物体
mg
v
沿光滑斜面下滑的物体
v
mg
N
沿粗糙斜面下滑的物体,拉力F大小和摩擦力 f 大小相等
v
mg
N
F
f
结论:
1)物体只受重力作用. (抛体运动)
2)物体除受重力外还受到其他力的作用,但其他力不做功,
或其他力做功的代数和为零.
不计阻力摆动的小球.
H
h
质量为m的小球,从离地面高H处自由下落到一轻弹簧上,弹簧长为L,弹簧压缩到最短时小球离地面高为h,忽略空气阻力,求:弹簧的最大弹性势能
弹簧最短时,弹性势能最大.只有重力和弹簧弹力做功,小球和弹簧系统机械能守恒.在最高点和最低点小球的动能为零,减少的重力势能等于增加的弹性势能.
竖直方向的弹簧振子,系统的机械能守恒吗?
判一判:下列情境中物体系统的机械能守恒吗?
乙
甲
A
B
C
A
沿光滑斜面下滑的木块
V0
F阻
G
匀速下降的降落伞
平抛运动
用细绳系一小球,使小球在竖直平面内做圆周运动
摆动的小球
(空气阻力不计)
小球落到弹簧上
如图所示,将小球从距斜轨底面h高处释放,使其沿竖直的圆轨道(半径为R)的内侧运动(不考虑空气阻力和摩擦阻力)
h
B
A
R
三、机械能守恒定律的应用
活动
1.若h < R,小球能否过圆形轨道的最高点,为什么?
2.若h =2R,小球能否过圆形轨道的最高点,为什么?
2.若h > 2R,小球能否一定过圆形轨道的最高点,为什么?
巩固练习:
1.关于机械能是否守恒,下列说法正确的是 ( )
A.做匀速直线运动的物体机械能一定守恒
B.做圆周运动的物体机械能一定守恒
C.做变速运动的物体机械能可能守恒
D.合外力对物体做功为零,机械能一定守恒
C
2.如图所示,木块均在固定的斜面上运动,其中图A、B、C中的斜面是光滑的,图D中的斜面是粗糙的,图A、B中的F为木块所受的外力,方向如图中箭头所示,图A、B、D中的木块向下运动,图C中的木块向上运动.在这四个图所示的运动过程中机械能守恒的是 ( )
C
3、质量分别为m和2m的两个小球A和B,中间用轻质杆相连,在杆的中点O处有一固定转动轴,把杆置于水平位置后释放,在B球顺时针摆动到最低位置的过程中 ( )
A.A球的重力势能增加,动能也增加,A球和地球组成的系统机械能不守恒
B.B球的重力势能减少,动能增加,B球和地球组成的系统机械能守恒
C.A球、B球和地球组成的系统机械能守恒
D.A球、B球和地球组成的系统机械不守恒
AC
4、光滑圆管形轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r<
(2)在小球从C端出来的瞬间,对管壁压力有哪几种典型情况,初速度v0各应满足什么条件?
v0>
刚好对管壁无压力
v0=
对下管壁有压力
v0>
5、用细绳悬挂一个质量为m的小球,悬点为O点,把小球拉至A点,使悬线与水平方向成30°角,由静止释放小球,问:小球运动到悬点的正下方B点时,细绳受到的拉力?
A
O
C
B
3.5mg
注意C点速度的突变,突变前后机械能不守恒
6、如图所示,小球A用不可伸长的轻绳悬于O点,在O点的正下方有一固定的钉子,OB=y.初始时,小球A与O同水平面,无初速释放A,绳长为L,且绳上最大拉力为11mg.为使球能绕B点做圆周运动且绳不断,求y的取值范围.
C点无速度的突变,机械能守恒
7、在高1.5 m的光滑平台上有一个质量为2 kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g取10 m/s2)( )
A.10 J
B.15 J
C.20 J
D.25 J
A
8、如图所示,一个质量m=0.2kg的光滑小球系于轻质弹簧的一端,且套在竖立的圆环上,弹簧的上端固定于环的最高点A,环的半径R=0.50m。弹簧的原长l0=0.5m,劲度系数为k=4.8N/m。若小球从图示位置B点由静止开始滑动到最低点C时,弹簧的弹性势能EP弹=0.6J,求:
(1)小球到C点时速度的大小;
(2)小球在C点对环的作用力.(g取10m/s2)
3m/s;3.2N,方向向下
9、一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量为2m和m的A、B两个小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆从水平位置由静止释放,转到竖直位置,在转动的过程中,忽略一切阻力.下列说法正确的是( )
A.杆转到竖直位置时,A、B两球的速度大小相等为
B.杆转到竖直位置时,杆对B球的作用力向上,
大小为(1/3)mg
C.杆转到竖直位置时,B球的机械能减少了(4/3)mgL
D.由于忽略一切摩擦阻力,A球机械能一定守恒
B
二、研究对象为两个物体
10、一轻质杆上有两个质量相等的小球A、B,轻杆可绕O点在竖直平面内自由转动.OA=OB=l,先将杆拉至水平面后由静止释放,则当轻杆转到竖直方向时,A、B两球的速度大小分别为多少?
三、验证机械能守恒定律实验
1.实验过程
(1)实验步骤
①安装:将打点计时器固定在铁架台上;用导线将打点计时器与低压交流电源相连接.
②接电源,打纸带:把纸带的一端在重物上用夹子固定好,另一端穿过打点计时器的限位孔,用手提着纸带使重物停靠在打点计时器附近,接通电源,待打点稳定后松开纸带,让重物自由下落.重复几次,打下3~5条纸带.
③选纸带:选取点迹较为清晰的.挑选纸带上第一个点及距离第一个点较远的点,并依次标上0,1,2,3,….
④数据测量:测出0到点1、点2、点3……的距离,即为对应的下落高度h1、h2、h3….
(2)数据处理
3.误差分析
(1)本实验的误差主要是由于纸带测量产生的偶然误差和重物、纸带运动中空气阻力及纸带与打点计时器摩擦阻力引起的系统误差,使动能的增加量稍小于势能的减少量.
(2)测量时采取多次测量求平均值来减小偶然误差,安装打点计时器时使两限位孔中线竖直,并且选择质量适当大些,体积尽量小些的重物来减小系统误差.
(3)打点计时器周期变化带来误差.
计算物体的速度,可有三种方法
第1种方法是根据机械能守恒定律得到的,而我们的目的就是验证机械能守恒定律,所以不能用
第2种方法认为加速度为g,由于各种摩擦阻力不可避免,所以实际加速度必将小于g,这样将得到机械能增加的结论,有阻力作用机械能应该是减少的,故这种方法也不能用
即时应用(即时突破,小试牛刀)
如图4-5-7是用自由落体法验证机械能守恒定律时得到的一条纸带.有关尺寸在图中已注明.我们选中n点来验证机械能守恒定律.下面举出了一些计算n点速度的方法,其中正确的是( )
图4-5-7
解析:选CD.vn应表示从(n-1)到(n+1)间的平均速度.C、D对,A、B错.
