分式方程
图片预览






文档简介
(共18张PPT)
阳信幸福中学 张延娥
分式方程的概念
解分式方程
1、已知分式 ,当x= 时,
分式无意义.
2、分式 与 的最简公分母
是 .
x2-1=0
x(x―3)
±1
2x(x―3)
复习旧知 来巩固
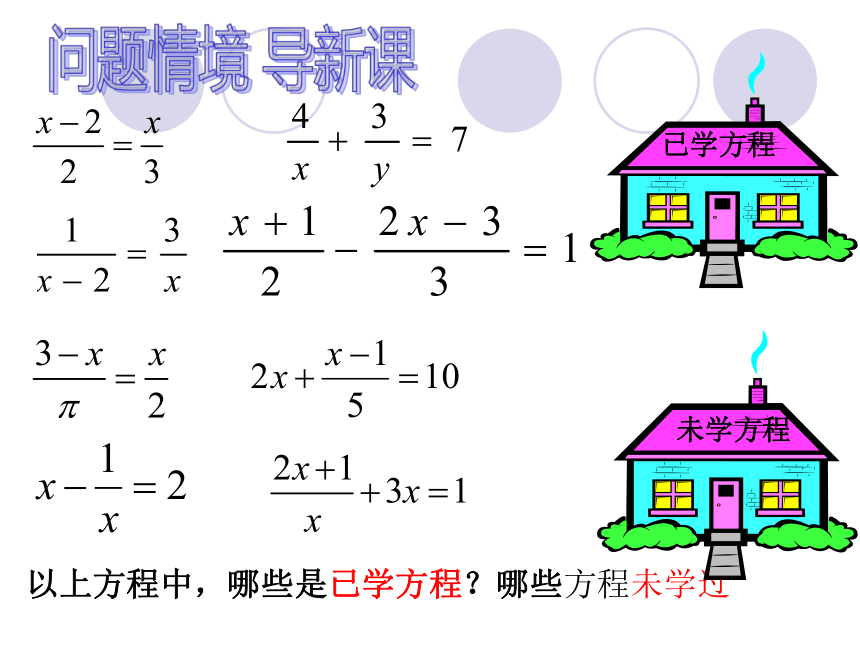
以上方程中,哪些是已学方程?哪些方程未学过
已学方程
未学方程
未学方程
他们有什么共同特点
分式方程
分母中含有未知数的方程,
叫做分式方程.
整式方程
1.判断下列哪些是分式方程?
及时反馈 我最棒
√
√
温故知新
解:去分母,得
3x=6+2x
解得: x=6
检验:将x=6代入原方程,得
左边=3=右边
所以,x=6是原方程的根.
我尝试
分式方程
整式方程
去分母
未学过
已学过
解答问题的途径-------
化未知为已知.
去分母
“转化”
7(x-2)=5x
方程两边都乘以最简公分母(x+1)(x-1)得,
x+1=2
解这个整式方程,得x=1.
把x=1代入原分式方程检验,结果x=1使分式方程式的分母的值为0 ,分式没有意义,因此x=1不是原分式方程的根。
在方程变形时,有时可能产生不适合原方程的根。
解分式方程必须验根!
怎样检验?
解:方程两边都乘以最简公分母 ( x-2)得
1-x =-1-2(x-2)
解这个方程,得
X=2
检验:当x=2时,原方程的分母
x-2=0,所以x=2不是原方程的根。
所以原方程无解。
解分式方程的一般步骤.
知识梳理 谈收获
去分母,化为整式方程:
解整式方程。
检验:
结论:
一化二解三检验
检验
分式方程的概念
解分式方程
实践作业,联系实际
根据以下方程自己编一道以植树活动为主题实际应用题.
阳信幸福中学 张延娥
分式方程的概念
解分式方程
1、已知分式 ,当x= 时,
分式无意义.
2、分式 与 的最简公分母
是 .
x2-1=0
x(x―3)
±1
2x(x―3)
复习旧知 来巩固
以上方程中,哪些是已学方程?哪些方程未学过
已学方程
未学方程
未学方程
他们有什么共同特点
分式方程
分母中含有未知数的方程,
叫做分式方程.
整式方程
1.判断下列哪些是分式方程?
及时反馈 我最棒
√
√
温故知新
解:去分母,得
3x=6+2x
解得: x=6
检验:将x=6代入原方程,得
左边=3=右边
所以,x=6是原方程的根.
我尝试
分式方程
整式方程
去分母
未学过
已学过
解答问题的途径-------
化未知为已知.
去分母
“转化”
7(x-2)=5x
方程两边都乘以最简公分母(x+1)(x-1)得,
x+1=2
解这个整式方程,得x=1.
把x=1代入原分式方程检验,结果x=1使分式方程式的分母的值为0 ,分式没有意义,因此x=1不是原分式方程的根。
在方程变形时,有时可能产生不适合原方程的根。
解分式方程必须验根!
怎样检验?
解:方程两边都乘以最简公分母 ( x-2)得
1-x =-1-2(x-2)
解这个方程,得
X=2
检验:当x=2时,原方程的分母
x-2=0,所以x=2不是原方程的根。
所以原方程无解。
解分式方程的一般步骤.
知识梳理 谈收获
去分母,化为整式方程:
解整式方程。
检验:
结论:
一化二解三检验
检验
分式方程的概念
解分式方程
实践作业,联系实际
根据以下方程自己编一道以植树活动为主题实际应用题.
