人教版八年级数学上册13.1.2线段的垂直平分线的性质课件(共21张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.1.2线段的垂直平分线的性质课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-25 21:06:22 | ||
图片预览








文档简介
解题利刃 垂直平分线
---垂直平分线的性质
公 路
在公路L的同侧,有两个贫困村庄A、B准备发展畜牧养殖业实现全面脱贫,为了精准扶贫便于两村的技术指导,政府计划在公路边上修建一所畜牧站,使得两个村的养殖户都没意见,问畜牧站应选在何处?你的方案是什么?
发现问题
L
A
B
教学目标:
理解和掌握线段的垂直平分线的定理,并能利用它们来进行证明或计算。
2. 了解数学和生活的紧密联系,培养用数学的能力。
轴对称的性质是什么?
作线段的垂直平分线
如何判断一条直线是否是线段的垂直平分线?
说一说 线段垂直平分线的性质.
不折叠图形,你能准确地作出轴对称图形的对称
轴吗?
作线段的垂直平分线
有时我们感觉两个平面图形是轴对称的,如何验
证呢?
在一张纸上任意画一条线段AB;
将纸对折,使线段端点A,B重合;
把纸展开,并画出折痕所在直线MN;
在MN上任取一点P,分别连接PA,PB;
将纸沿着MN对折,量一量,折一折,观察PA和PB,有什么发现?
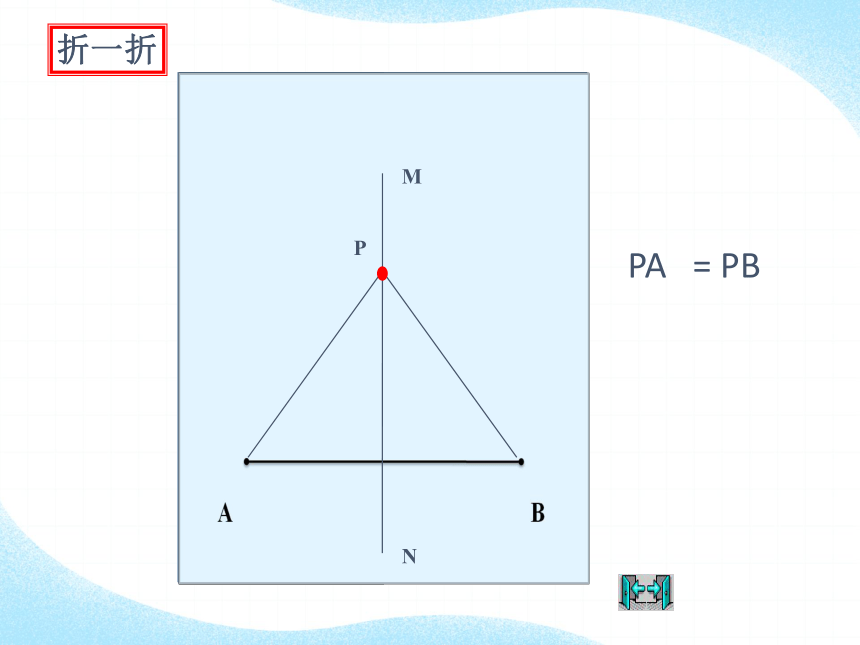
折一折
(B)
A
B
N
M
P
折一折
PA = PB
猜想:线段垂直平分线上的点与这条线段两个端点的距离相等.
题设:
结论:
大胆猜想
这个点与这条线段两个端点距离相等
一个点在线段的垂直平分线上
几何语言表示为:
∵ CA =CB,l⊥AB于点C,点P在l上
∴ PA =PB.
A
B
P
C
l
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
证明:∵l⊥AB
∴ ∠ PCA= ∠ PCB=90°
在 ΔPAC和Δ PBC中,
AC=BC
∠ PCA= ∠ PCB
PC=PC
∴ ΔPAC ≌Δ PBC(SAS)
∴PA=PB
验证猜想
得出定理
1、如图直线MN垂直平分线段AB,则AE=AF。
判断题
2、如图线段MN被直线AB垂直平分,则ME=NE。
A
B
F
E
N
M
B
A
公 路
在公路L的同侧,有两个贫困村庄A、B准备发展畜牧养殖业实现全面脱贫,为了精准扶贫便于两村的技术指导,政府计划在公路边上修建一所畜牧站,使得两个村的养殖户都没意见,问畜牧站应选在何处?你的方案是什么?
解决问题
L
1、如图所示,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长是( )
A.3.9 cm B.7.8 cm
C.4 cm D.4.6 cm
夯实基础
B
例1、如图所示,在三角形ABC中 ,AB=AC=14cm,AB边的垂直平分线DE交AC于点D,
解:
∵DE垂直平分AB
∴AD=BD.(线段垂直平分线上的点到线段两个端点距离相等)
∴BD+BC+CD=AD+CD+BC=24
∵AB=AC=14
即AD+CD=AC=14,
又∵AD+CD+BC=24
∴BC=24-14=10cm
答:BC的长为10cm。
例题解析
BC的长为10cm,求△DBC的周长
△DBC的周长是24cm,求BC的长。
A
D
B
C
M
挑战自我
将军
城堡
认真思考哦!
必做: 1. 课本 P65 习题13.1 6题
2. 同步学习 P25基础自测
3. 预习课本 P62-63
选作: 1. 课本 P66习题12.1 12题
2.同步学习 P25拓展提高
3、已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P在AC的垂直平分线上;
B
A
C
M
N
M’
N’
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
∵PA=PC
∴点P在AC的垂直平分线上
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。(外心)
能力提升
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
(4)经过已知直线外一点作这条直线的垂线.
那么利用尺规还能解决什么作图问题呢?
作线段的垂直平分线
我们已能用尺规完成:
这种作法的依据是什么?
这种作图方法还有哪些作用?
确定线段的中点.
作法:如图.
(1)分别以点A,B 为圆心,以大于 AB的长为半径
作弧,两弧相交于C,D 两点;
(2)作直线CD.
CD 就是所求作的直线.
作线段的垂直平分线
怎样作线段AB 的垂直平分线呢?
A
B
C
D
作轴对称图形的对称轴
如果两个图形成轴对称,怎样作出图形的对称轴?
如果两个图形成轴对称,其对称轴是任何一对对应
点所连线段的垂直平分线.因此,只要找到任意一组对
应点,作出对应点所连线段的垂直平分线,就得到此图
形的对称轴.
作轴对称图形的对称轴
如图中的五角星,请作出它的一条对称轴.
五角星的对称轴有什么特点?
作轴对称图形的对称轴
你能作出这个五角星的其他对称轴吗?它共有几条
对称轴?
相交于一点.
---垂直平分线的性质
公 路
在公路L的同侧,有两个贫困村庄A、B准备发展畜牧养殖业实现全面脱贫,为了精准扶贫便于两村的技术指导,政府计划在公路边上修建一所畜牧站,使得两个村的养殖户都没意见,问畜牧站应选在何处?你的方案是什么?
发现问题
L
A
B
教学目标:
理解和掌握线段的垂直平分线的定理,并能利用它们来进行证明或计算。
2. 了解数学和生活的紧密联系,培养用数学的能力。
轴对称的性质是什么?
作线段的垂直平分线
如何判断一条直线是否是线段的垂直平分线?
说一说 线段垂直平分线的性质.
不折叠图形,你能准确地作出轴对称图形的对称
轴吗?
作线段的垂直平分线
有时我们感觉两个平面图形是轴对称的,如何验
证呢?
在一张纸上任意画一条线段AB;
将纸对折,使线段端点A,B重合;
把纸展开,并画出折痕所在直线MN;
在MN上任取一点P,分别连接PA,PB;
将纸沿着MN对折,量一量,折一折,观察PA和PB,有什么发现?
折一折
(B)
A
B
N
M
P
折一折
PA = PB
猜想:线段垂直平分线上的点与这条线段两个端点的距离相等.
题设:
结论:
大胆猜想
这个点与这条线段两个端点距离相等
一个点在线段的垂直平分线上
几何语言表示为:
∵ CA =CB,l⊥AB于点C,点P在l上
∴ PA =PB.
A
B
P
C
l
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
证明:∵l⊥AB
∴ ∠ PCA= ∠ PCB=90°
在 ΔPAC和Δ PBC中,
AC=BC
∠ PCA= ∠ PCB
PC=PC
∴ ΔPAC ≌Δ PBC(SAS)
∴PA=PB
验证猜想
得出定理
1、如图直线MN垂直平分线段AB,则AE=AF。
判断题
2、如图线段MN被直线AB垂直平分,则ME=NE。
A
B
F
E
N
M
B
A
公 路
在公路L的同侧,有两个贫困村庄A、B准备发展畜牧养殖业实现全面脱贫,为了精准扶贫便于两村的技术指导,政府计划在公路边上修建一所畜牧站,使得两个村的养殖户都没意见,问畜牧站应选在何处?你的方案是什么?
解决问题
L
1、如图所示,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长是( )
A.3.9 cm B.7.8 cm
C.4 cm D.4.6 cm
夯实基础
B
例1、如图所示,在三角形ABC中 ,AB=AC=14cm,AB边的垂直平分线DE交AC于点D,
解:
∵DE垂直平分AB
∴AD=BD.(线段垂直平分线上的点到线段两个端点距离相等)
∴BD+BC+CD=AD+CD+BC=24
∵AB=AC=14
即AD+CD=AC=14,
又∵AD+CD+BC=24
∴BC=24-14=10cm
答:BC的长为10cm。
例题解析
BC的长为10cm,求△DBC的周长
△DBC的周长是24cm,求BC的长。
A
D
B
C
M
挑战自我
将军
城堡
认真思考哦!
必做: 1. 课本 P65 习题13.1 6题
2. 同步学习 P25基础自测
3. 预习课本 P62-63
选作: 1. 课本 P66习题12.1 12题
2.同步学习 P25拓展提高
3、已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P在AC的垂直平分线上;
B
A
C
M
N
M’
N’
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
∵PA=PC
∴点P在AC的垂直平分线上
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。(外心)
能力提升
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
(4)经过已知直线外一点作这条直线的垂线.
那么利用尺规还能解决什么作图问题呢?
作线段的垂直平分线
我们已能用尺规完成:
这种作法的依据是什么?
这种作图方法还有哪些作用?
确定线段的中点.
作法:如图.
(1)分别以点A,B 为圆心,以大于 AB的长为半径
作弧,两弧相交于C,D 两点;
(2)作直线CD.
CD 就是所求作的直线.
作线段的垂直平分线
怎样作线段AB 的垂直平分线呢?
A
B
C
D
作轴对称图形的对称轴
如果两个图形成轴对称,怎样作出图形的对称轴?
如果两个图形成轴对称,其对称轴是任何一对对应
点所连线段的垂直平分线.因此,只要找到任意一组对
应点,作出对应点所连线段的垂直平分线,就得到此图
形的对称轴.
作轴对称图形的对称轴
如图中的五角星,请作出它的一条对称轴.
五角星的对称轴有什么特点?
作轴对称图形的对称轴
你能作出这个五角星的其他对称轴吗?它共有几条
对称轴?
相交于一点.
