人教版九年级上册数学24.2.2直线与圆的位置关系 课件(14张PPT)
文档属性
| 名称 | 人教版九年级上册数学24.2.2直线与圆的位置关系 课件(14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 996.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-26 00:00:00 | ||
图片预览




文档简介
人教九上数学24.2.2
直线与圆的位置关系
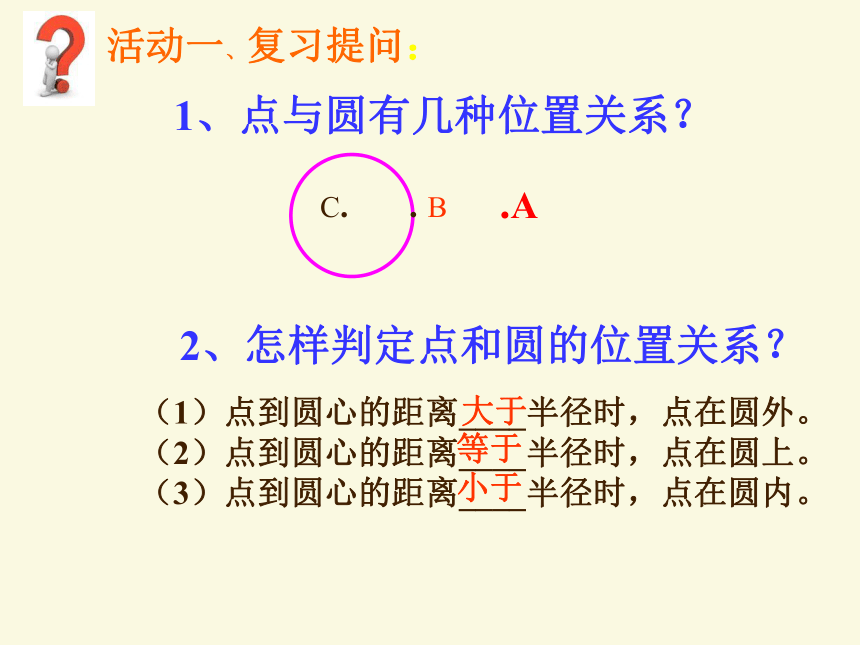
1、点与圆有几种位置关系?
活动一、复习提问:
2、怎样判定点和圆的位置关系?
. B
C.
(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。
大于
等于
小于
.A
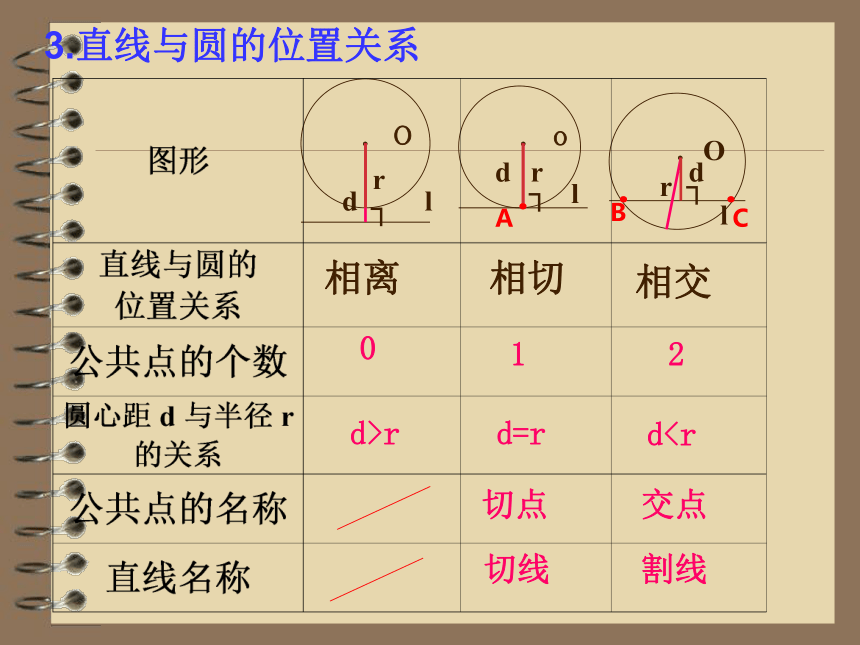
3.直线与圆的位置关系
0
d>r
1
d=r
切点
切线
2
d交点
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
4.怎样判定直线 与圆的位置关系?
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________
的关系来判断。
在实际应用中,常采用第二种方法判定。
直线 与圆的公共点
圆心到直线的距离d与半径r
例题1.圆的直径是8cm,如果直线与圆心的距离分别是
(1)3cm ; (2)4cm ; (3) 5cm,
那么直线与圆分别是什么位置关系? 有几个公共点?
(3)圆心距 d=5cm>r = 4cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
(2)圆心距 d=4cm = r = 4cm 直线与圆相切,
解 (1) 圆心距 d=3cm< r = 4cm 直线与圆相交,
活动二:相关题型讲解
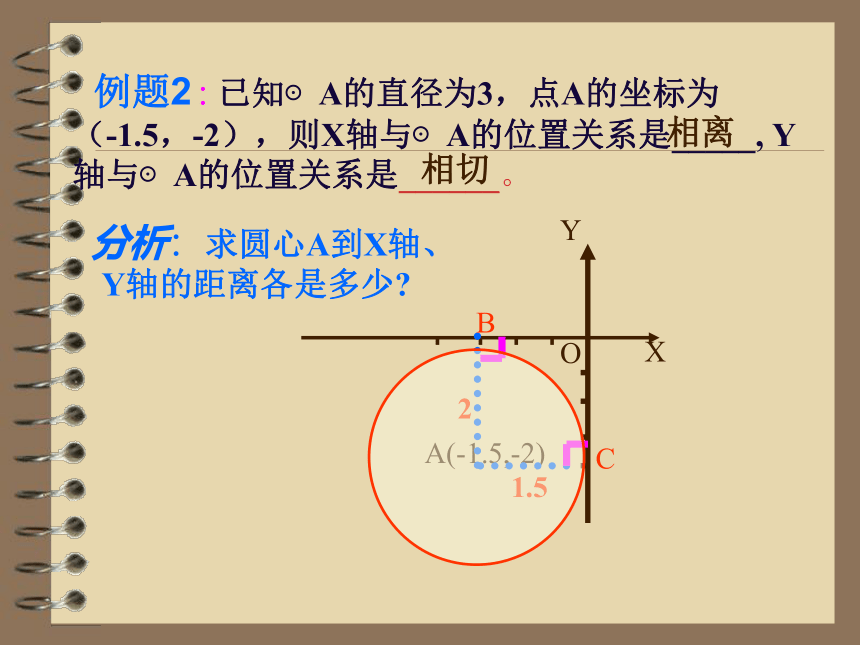
分析:求圆心A到X轴、
Y轴的距离各是多少?
A(-1.5,-2)
O
X
Y
例题2 : 已知⊙A的直径为3,点A的坐标为
(-1.5,-2),则X轴与⊙A的位置关系是_____, Y 轴与⊙A的位置关系是______。
B
C
2
1.5
相离
相切
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。
B
C
A
4
5
3
例题3
分析:根据直线与圆的位置关系的数量特征,要确定圆心C与直线AB的位置关系必须用圆心到直线的距离d与半径r的大小进行比较;
即确定圆心C到直线AB的距离d。
即圆心C到AB的距离d=2.4cm。
(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。
(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。
(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。
解:过C作CD⊥AB,垂足为D。
在Rt△ABC中,
AB= =
=5(cm)
根据三角形面积公式有
CD·AB=AC·BC
∴CD= =
2
2
2
2
=2.4(cm)。
A
B
C
A
D
4
5
3
d=2.4
例题4.若⊙O与直线m的距离为d,⊙O 的半径为r,若d,
r是方程 的两个根,
且直线m与⊙O相切,
求 的值。
分析:直线m与⊙O相切,则d=r,即方程有两相等的实数根即?=0
解:据题意可得:方程中的?=0
即
解得 = - 2
如图:在射线OB上取一点M,OM=10cm,以M为圆心作一直径为10cm的⊙M,试问:过O的射线OA与OB所夹的锐角β取什么值时射线OA与⊙M : (1)相交, (2)相切 (3)相离
例题5
分析:这道题是上面题目的逆反应用,⊙M为一定圆,射线
OA为一动线,我们可以从特殊到一般,看当β为多少时
⊙M与OA相切,即点M到OA的距离MN=5=r时,OM=10,则β为30°.
解(1)当β<30°时,⊙M与OA相交
(2)当β=30°时,MN=d=r=5cm,
⊙M与OA相切
(3)当β>30°时,⊙M与OA相离
10
动动脑筋
1. 已知⊙O的直径是8cm,点O到直线?的距离
是4cm,则⊙O与直线?的位置关系是 ___ _;
直线?与⊙O的公共点个数是____.
2. 直线?上一点A到圆心O的距离等于⊙O的半径,
则直线?与⊙O的位置关系是 。
活动三:大家动手,做一做
3.⊙O的半径为3 ,圆心O到直线m的距离为d,若直线m
与⊙O没有公共点,则d的范围
5. 若⊙O与直线?的距离为d,⊙O 的半径为r,若d,r是方程
的两个根,则直线?与⊙O的位置关系是.
的两个根,且直线m与⊙O的
6. 若d,r是方程
位置关系是相切,则α的值。
答案:1.相切,一个; 2.相切或相交; 3.d>3;
4.(1)相离,(2)r>12cm, (3)60/13cm;
5.相离或相交; 6.α=9
4.如图,在Rt△ABC中,∠C=90°,AB=13cm,AC=5cm,
⑴ 以A为圆心,4cm的长为半径的⊙A与直线BC的位置关系是 . ⑵ 以B为圆心的⊙B与直线AC相交,则⊙B的半径r的取值范围是.
⑶ 以C为圆心,r为半径的⊙C与直线AB相切,则r的长应为?
A
C
B
13
5
┐
小结
(1)本节课重点是:进一步学习如何确定圆与直线的位置关系,通过交点个数或d与r的比较进一步体现了量化与比较这两种思想在数学中的应用。
(2)本节课的难点是:在d与r的比较中确定好变量与定量的关系。
直线与圆的位置关系
1、点与圆有几种位置关系?
活动一、复习提问:
2、怎样判定点和圆的位置关系?
. B
C.
(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。
大于
等于
小于
.A
3.直线与圆的位置关系
0
d>r
1
d=r
切点
切线
2
d
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
4.怎样判定直线 与圆的位置关系?
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________
的关系来判断。
在实际应用中,常采用第二种方法判定。
直线 与圆的公共点
圆心到直线的距离d与半径r
例题1.圆的直径是8cm,如果直线与圆心的距离分别是
(1)3cm ; (2)4cm ; (3) 5cm,
那么直线与圆分别是什么位置关系? 有几个公共点?
(3)圆心距 d=5cm>r = 4cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
(2)圆心距 d=4cm = r = 4cm 直线与圆相切,
解 (1) 圆心距 d=3cm< r = 4cm 直线与圆相交,
活动二:相关题型讲解
分析:求圆心A到X轴、
Y轴的距离各是多少?
A(-1.5,-2)
O
X
Y
例题2 : 已知⊙A的直径为3,点A的坐标为
(-1.5,-2),则X轴与⊙A的位置关系是_____, Y 轴与⊙A的位置关系是______。
B
C
2
1.5
相离
相切
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。
B
C
A
4
5
3
例题3
分析:根据直线与圆的位置关系的数量特征,要确定圆心C与直线AB的位置关系必须用圆心到直线的距离d与半径r的大小进行比较;
即确定圆心C到直线AB的距离d。
即圆心C到AB的距离d=2.4cm。
(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。
(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。
(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。
解:过C作CD⊥AB,垂足为D。
在Rt△ABC中,
AB= =
=5(cm)
根据三角形面积公式有
CD·AB=AC·BC
∴CD= =
2
2
2
2
=2.4(cm)。
A
B
C
A
D
4
5
3
d=2.4
例题4.若⊙O与直线m的距离为d,⊙O 的半径为r,若d,
r是方程 的两个根,
且直线m与⊙O相切,
求 的值。
分析:直线m与⊙O相切,则d=r,即方程有两相等的实数根即?=0
解:据题意可得:方程中的?=0
即
解得 = - 2
如图:在射线OB上取一点M,OM=10cm,以M为圆心作一直径为10cm的⊙M,试问:过O的射线OA与OB所夹的锐角β取什么值时射线OA与⊙M : (1)相交, (2)相切 (3)相离
例题5
分析:这道题是上面题目的逆反应用,⊙M为一定圆,射线
OA为一动线,我们可以从特殊到一般,看当β为多少时
⊙M与OA相切,即点M到OA的距离MN=5=r时,OM=10,则β为30°.
解(1)当β<30°时,⊙M与OA相交
(2)当β=30°时,MN=d=r=5cm,
⊙M与OA相切
(3)当β>30°时,⊙M与OA相离
10
动动脑筋
1. 已知⊙O的直径是8cm,点O到直线?的距离
是4cm,则⊙O与直线?的位置关系是 ___ _;
直线?与⊙O的公共点个数是____.
2. 直线?上一点A到圆心O的距离等于⊙O的半径,
则直线?与⊙O的位置关系是 。
活动三:大家动手,做一做
3.⊙O的半径为3 ,圆心O到直线m的距离为d,若直线m
与⊙O没有公共点,则d的范围
5. 若⊙O与直线?的距离为d,⊙O 的半径为r,若d,r是方程
的两个根,则直线?与⊙O的位置关系是.
的两个根,且直线m与⊙O的
6. 若d,r是方程
位置关系是相切,则α的值。
答案:1.相切,一个; 2.相切或相交; 3.d>3;
4.(1)相离,(2)r>12cm, (3)60/13cm;
5.相离或相交; 6.α=9
4.如图,在Rt△ABC中,∠C=90°,AB=13cm,AC=5cm,
⑴ 以A为圆心,4cm的长为半径的⊙A与直线BC的位置关系是 . ⑵ 以B为圆心的⊙B与直线AC相交,则⊙B的半径r的取值范围是.
⑶ 以C为圆心,r为半径的⊙C与直线AB相切,则r的长应为?
A
C
B
13
5
┐
小结
(1)本节课重点是:进一步学习如何确定圆与直线的位置关系,通过交点个数或d与r的比较进一步体现了量化与比较这两种思想在数学中的应用。
(2)本节课的难点是:在d与r的比较中确定好变量与定量的关系。
同课章节目录
