人教版数学九年级上册课件: 23.2.2中心对称图形(39张PPT)
文档属性
| 名称 | 人教版数学九年级上册课件: 23.2.2中心对称图形(39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-25 00:00:00 | ||
图片预览







文档简介
23.2.2 中心对称图形
【知识与能力】
理解关于中心对称的两个图形是全等图形。
掌握这两个性质的运用。
了解中心对称图形及对称中心的概念及其它们的应用。
能正确区分中心对称与中心对称图形。
教学目标
中心对称的两条基本性质及其运用。
中心对称图形的有关概念及其它们的运用。
区别关于中心对称的两个图形和中心对称图形。
教学重难点
这三个图形各自旋转180°后都能与本身重合。
新课导入
从图形变换的角度考虑,这些图形有什么共同的特征?
O
B
A
C
D
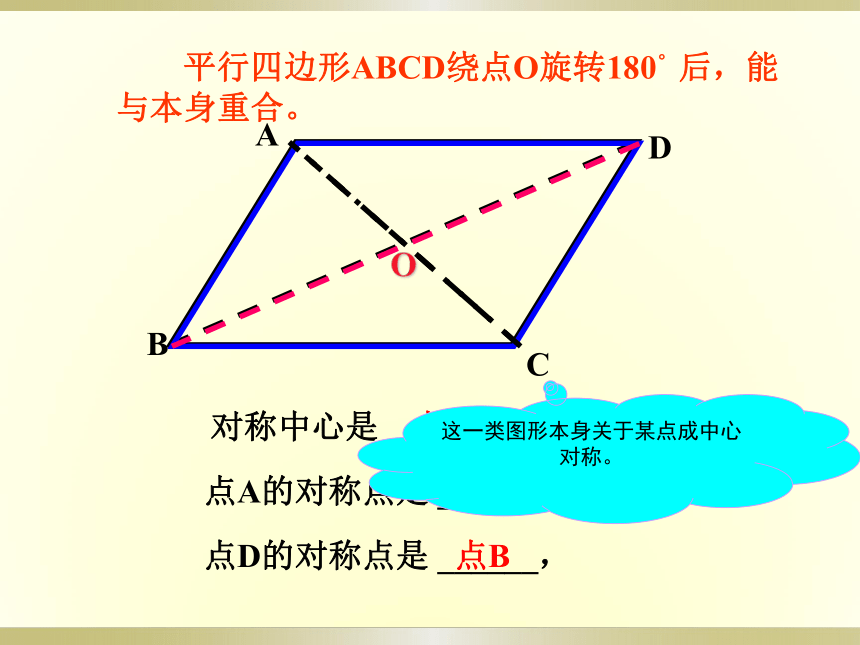
对称中心是 ______,
点O
点A的对称点是 ______,
点D的对称点是 ______,
点C
点B
平行四边形ABCD绕点O旋转180°后,能与本身重合。
这一类图形本身关于某点成中心对称。
东方明珠
多么漂亮的建筑啊!
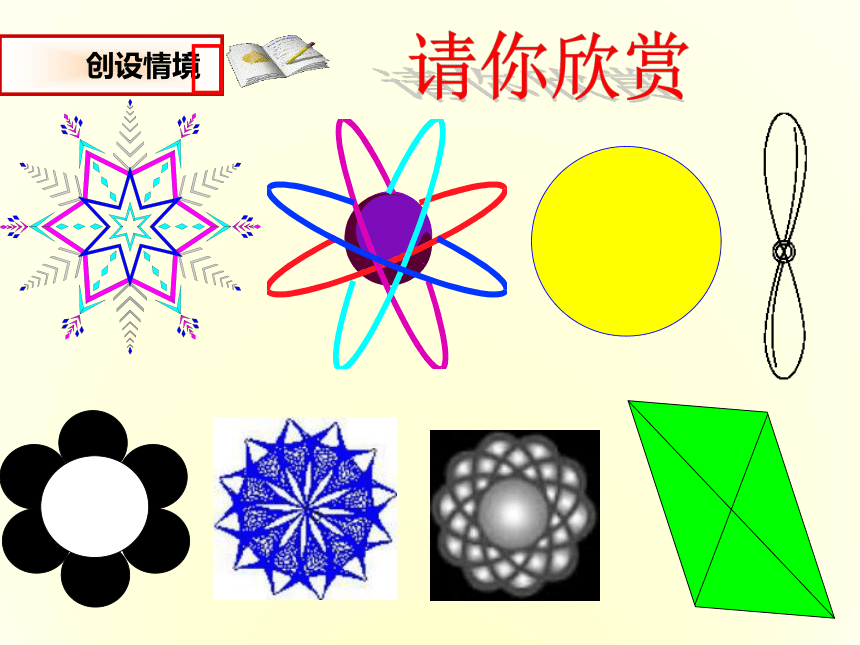
请你欣赏
创设情境
o
(2)圆
(4) 正方形
(1)线段
(3)平行四边形
A
B
观 察
将下面的图形绕O点旋转180°,你有什么发现?
O
O
O
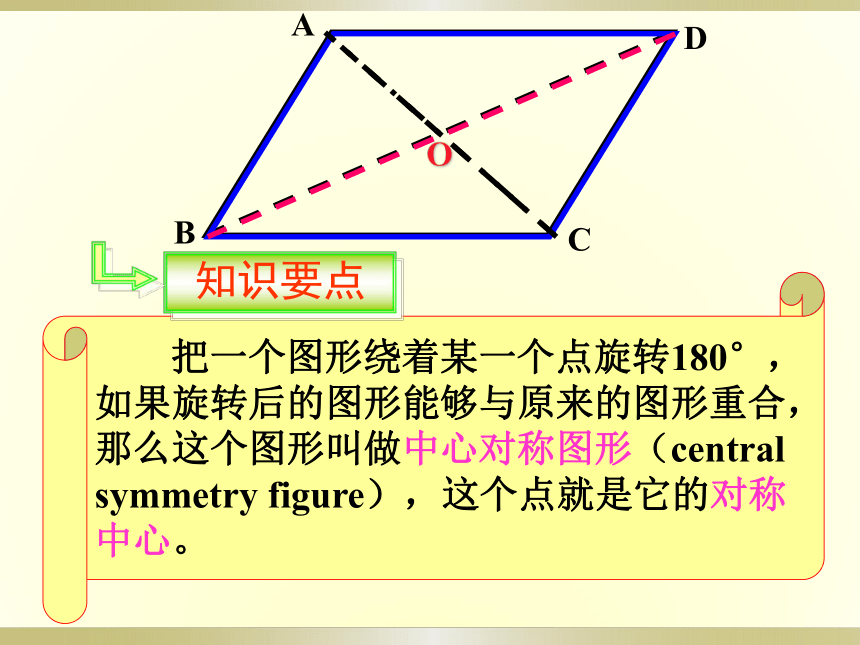
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形(central symmetry figure),这个点就是它的对称中心。
知识要点
O
B
A
C
D
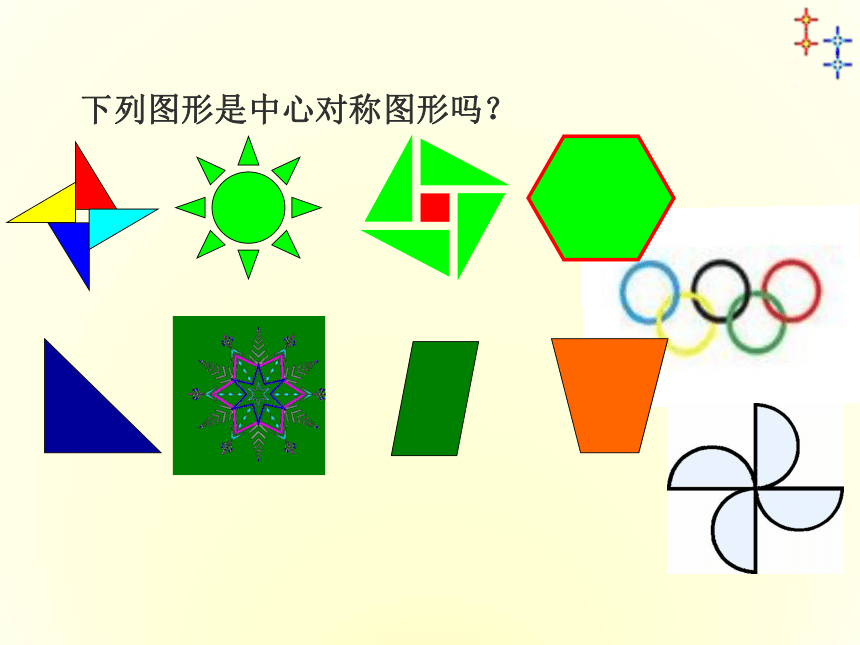
下列图形是中心对称图形吗?
认真观察旋转180°后……
都是中心对称图形。
图形的中心就是对称中心。
都是中心对称图形。
图形的中心就是对称中心。
求证:具有对称中心的四边形是平行四边形。
证明:O是四边形ABCD的对称中心,
根据中心对称性质,线段AC、BD必过点O,
且AO=CO,BO=DO,
即四边形ABCD的对角线互相平分,
因此,四边形ABCD是平行四边形。
例题
讨论:一个中心对称图形有多少个对称中心?
理性提升
1、直线无数个对称中心
2、其它中心对称图形只有一个对称中心。
思考:
对称点的连线与对称中心有什么关系?
中心对称图形的性质:
对称点所连线段都经过对称中心,而且被对称中心平分
探究性质
理性提升
F
E
D
C
B
A
一个中心对称图形中对称点连线的交点或对称点连线的中点就是对称中心
理性提升
思考:根据性质,我们可以利用什么方法找对称中心?
中心对称与中心对称图形是两个既有联系又有
区别的概念
区别: 中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称
联系: 如果将中心对称图形的两个图形看成一个整体,
则它们是中心对称图形
如果将中心对称图形,把对称的部分看成两个图形,则它们是关于中心对称。
对比1
理性提升
旋转前后的图形完全重合
轴对称图形
中心对称图形
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折(翻转
180°
)
图形绕对称中心旋转
180°
翻转前后的图形完全重合
中心对称图形与轴对称图形的区别与联系
课堂小结
名称
中心对称
中心对称图形
定义
性质
区别
联系
中心对称与中心对称图形的区别与联系
把一个图形绕着某一个点旋转180?,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点
如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
________
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两图,则它们成中心对称。若把中心对称的两图看作一个整体,则成为中心对称图形。
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
角
等腰三角形
等边三角形
平行四边形
矩行
菱行
正方形
轴对称图形与中心对称图形的比较
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
2条
中点
角
1条
等腰三角形
1条
等边三角形
3条
平行四边形
对角线交点
矩行
2条
对角线交点
菱行
2条
对角线交点
正方形
4条
对角线交点
轴对称图形与中心对称图形的比较
1.通过旋转平行四边形,你能验证平行四边形的哪些性质?
90度或其整数倍
平行四边形对边相等、对角相等、对角线互相平分.
正方形的四边相等、四角相等、对角线垂直平分且相等.
议一议
2.正方形是中心对称图形吗?
是!
正方形绕两条对角线的交点旋转多少度 能与原来的图形重合?
能由此验证正方形的一些特殊性质吗?
1.我们学过的菱形、矩形、正方形、等腰梯形、
正三角形也都是中心对称图形吗?
2.还有哪些多边形是中心对称图形呢?
结论:中心对称的多边形很多,如边数为偶数的
正多边形都是中心对称图形.
想一想
这些图形是中心对称图形的有( )
——————————————————
⑹
⑺
⑽
⑶
⑴
⑸
⑹
⑷
⑻
⑾
⑿
⑺
⑸
⑼
⑽
⑼
⑿
练一练
这些图形中既是中心对称图形又是轴对称图形的是__________.
A
B
C
F
E
D
B、
D
1、在一次游戏当中,小明将图1的四张扑克牌中的一张旋转180O后,得到图2,小亮看完,很快知道小明旋转了哪一张扑克,你知道为什么吗?
图1
图2
旋转了方块J,因为其它三张均不是中心对称图形,若旋转了就和会图1不同,而方块J即使旋转了也和图1相同.
随堂练习
A B C E S O W N I x Y Z
2、下列这些字母中有_____个是中心对称的图形.
下列这些数字中有_____个是中心对称的图形.
有_____个是轴对称的图形.
有_____个是轴对称的图形.
6
9
5
4
随堂练习
1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形
C
(2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
A
随堂练习
2. 判断下列说法是否正确。
(1)轴对称图形也是中心对称图形。( )
(2)旋转对称图形也是中心对称图形。( )
(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( )
(4)角是轴对称图形也是中心对称图形。( )
(5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )
×
√
×
√
×
3. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(1)
(3)
(2)
(4)
(5)
(6)
(3)(4)(6)
(1)
(2)(5)
4. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨
①②③④
①⑥⑦⑧⑨
⑥⑦⑧⑨
5. 正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?
边数为偶数的正多边形都是中心对称图形。
√
×
√
×
中考链接
1.
B
C
世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有轴对称和中心对称性.
一石激起千层浪
你认识这些名车标志吗?
宝马
阿尔法. 罗米欧
奥迪
重庆长安
反思
1.回顾本节课的活动过程.
2.本节课学到了哪些知识?
——应用
(2)中心对称图形的应用
观察
——分析
——探索
——概括
(1)中心对称图形的定义与性质
再见
【知识与能力】
理解关于中心对称的两个图形是全等图形。
掌握这两个性质的运用。
了解中心对称图形及对称中心的概念及其它们的应用。
能正确区分中心对称与中心对称图形。
教学目标
中心对称的两条基本性质及其运用。
中心对称图形的有关概念及其它们的运用。
区别关于中心对称的两个图形和中心对称图形。
教学重难点
这三个图形各自旋转180°后都能与本身重合。
新课导入
从图形变换的角度考虑,这些图形有什么共同的特征?
O
B
A
C
D
对称中心是 ______,
点O
点A的对称点是 ______,
点D的对称点是 ______,
点C
点B
平行四边形ABCD绕点O旋转180°后,能与本身重合。
这一类图形本身关于某点成中心对称。
东方明珠
多么漂亮的建筑啊!
请你欣赏
创设情境
o
(2)圆
(4) 正方形
(1)线段
(3)平行四边形
A
B
观 察
将下面的图形绕O点旋转180°,你有什么发现?
O
O
O
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形(central symmetry figure),这个点就是它的对称中心。
知识要点
O
B
A
C
D
下列图形是中心对称图形吗?
认真观察旋转180°后……
都是中心对称图形。
图形的中心就是对称中心。
都是中心对称图形。
图形的中心就是对称中心。
求证:具有对称中心的四边形是平行四边形。
证明:O是四边形ABCD的对称中心,
根据中心对称性质,线段AC、BD必过点O,
且AO=CO,BO=DO,
即四边形ABCD的对角线互相平分,
因此,四边形ABCD是平行四边形。
例题
讨论:一个中心对称图形有多少个对称中心?
理性提升
1、直线无数个对称中心
2、其它中心对称图形只有一个对称中心。
思考:
对称点的连线与对称中心有什么关系?
中心对称图形的性质:
对称点所连线段都经过对称中心,而且被对称中心平分
探究性质
理性提升
F
E
D
C
B
A
一个中心对称图形中对称点连线的交点或对称点连线的中点就是对称中心
理性提升
思考:根据性质,我们可以利用什么方法找对称中心?
中心对称与中心对称图形是两个既有联系又有
区别的概念
区别: 中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称
联系: 如果将中心对称图形的两个图形看成一个整体,
则它们是中心对称图形
如果将中心对称图形,把对称的部分看成两个图形,则它们是关于中心对称。
对比1
理性提升
旋转前后的图形完全重合
轴对称图形
中心对称图形
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折(翻转
180°
)
图形绕对称中心旋转
180°
翻转前后的图形完全重合
中心对称图形与轴对称图形的区别与联系
课堂小结
名称
中心对称
中心对称图形
定义
性质
区别
联系
中心对称与中心对称图形的区别与联系
把一个图形绕着某一个点旋转180?,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点
如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
________
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两图,则它们成中心对称。若把中心对称的两图看作一个整体,则成为中心对称图形。
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
角
等腰三角形
等边三角形
平行四边形
矩行
菱行
正方形
轴对称图形与中心对称图形的比较
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
2条
中点
角
1条
等腰三角形
1条
等边三角形
3条
平行四边形
对角线交点
矩行
2条
对角线交点
菱行
2条
对角线交点
正方形
4条
对角线交点
轴对称图形与中心对称图形的比较
1.通过旋转平行四边形,你能验证平行四边形的哪些性质?
90度或其整数倍
平行四边形对边相等、对角相等、对角线互相平分.
正方形的四边相等、四角相等、对角线垂直平分且相等.
议一议
2.正方形是中心对称图形吗?
是!
正方形绕两条对角线的交点旋转多少度 能与原来的图形重合?
能由此验证正方形的一些特殊性质吗?
1.我们学过的菱形、矩形、正方形、等腰梯形、
正三角形也都是中心对称图形吗?
2.还有哪些多边形是中心对称图形呢?
结论:中心对称的多边形很多,如边数为偶数的
正多边形都是中心对称图形.
想一想
这些图形是中心对称图形的有( )
——————————————————
⑹
⑺
⑽
⑶
⑴
⑸
⑹
⑷
⑻
⑾
⑿
⑺
⑸
⑼
⑽
⑼
⑿
练一练
这些图形中既是中心对称图形又是轴对称图形的是__________.
A
B
C
F
E
D
B、
D
1、在一次游戏当中,小明将图1的四张扑克牌中的一张旋转180O后,得到图2,小亮看完,很快知道小明旋转了哪一张扑克,你知道为什么吗?
图1
图2
旋转了方块J,因为其它三张均不是中心对称图形,若旋转了就和会图1不同,而方块J即使旋转了也和图1相同.
随堂练习
A B C E S O W N I x Y Z
2、下列这些字母中有_____个是中心对称的图形.
下列这些数字中有_____个是中心对称的图形.
有_____个是轴对称的图形.
有_____个是轴对称的图形.
6
9
5
4
随堂练习
1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形
C
(2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
A
随堂练习
2. 判断下列说法是否正确。
(1)轴对称图形也是中心对称图形。( )
(2)旋转对称图形也是中心对称图形。( )
(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( )
(4)角是轴对称图形也是中心对称图形。( )
(5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )
×
√
×
√
×
3. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(1)
(3)
(2)
(4)
(5)
(6)
(3)(4)(6)
(1)
(2)(5)
4. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨
①②③④
①⑥⑦⑧⑨
⑥⑦⑧⑨
5. 正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?
边数为偶数的正多边形都是中心对称图形。
√
×
√
×
中考链接
1.
B
C
世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有轴对称和中心对称性.
一石激起千层浪
你认识这些名车标志吗?
宝马
阿尔法. 罗米欧
奥迪
重庆长安
反思
1.回顾本节课的活动过程.
2.本节课学到了哪些知识?
——应用
(2)中心对称图形的应用
观察
——分析
——探索
——概括
(1)中心对称图形的定义与性质
再见
同课章节目录
