江西省宜春市宜丰县第二中学2019_2020学年高二数学下学期期末考试试题理(Word含答案)
文档属性
| 名称 | 江西省宜春市宜丰县第二中学2019_2020学年高二数学下学期期末考试试题理(Word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 938.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-25 19:22:53 | ||
图片预览




文档简介
江西省宜春市宜丰县第二中学2019-2020学年高二数学下学期期末考试试题 理
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合M={x|0A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知全集为,集合,,则( )
A. B. C. D.
3.已知函数是定义在R上的奇函数,且当时,,则( )
A.2 B.4 C.-2 D.-4
4.设随机变量X~B,则P(X=3)等于( )
A. B. C. D.
5.有下列四个条件:①,,; ②,;③,,; ④、是异面直线,,,。
其中能保证直线//平面的条件是( )
A.①② B.①③ C.①④ D.②④
6. 若且满足,则的最小值是( )
A. B. C.7 D.6
7. 从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件“第一次取到的是奇数”,“第二次取到的是奇数”,则???????
A. B. C. D.
8. 有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 非优秀 总计
甲班 10 b
乙班 c 30
总计
105
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
附:,
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
9. 某学校安排甲、乙、丙、丁四位同学参加数学、物理、化学竞赛,要求每位同学仅报一科,每科至少有一位同学参加,且甲、乙不能参加同一学科,则不同的安排方法有( )
A.36种 B.30种 C.24种 D.6种
某几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
11.已知函数是单调函数,且时,都有,则( ).
A.-4 B.-3 C.-1 D.0
12.设函数,则使得成立的的取值范围是( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
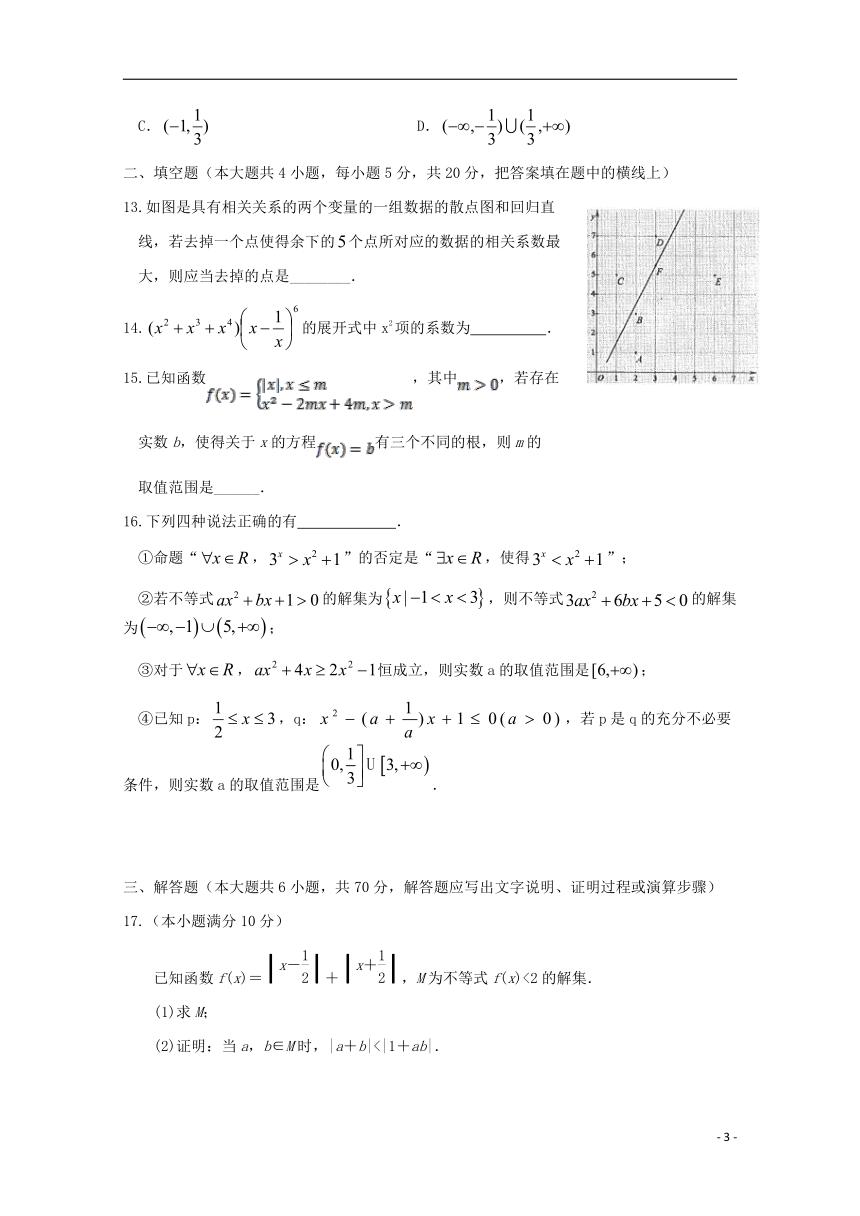
13.如图是具有相关关系的两个变量的一组数据的散点图和回归直
线,若去掉一个点使得余下的个点所对应的数据的相关系数最
大,则应当去掉的点是________.
14.的展开式中x2项的系数为 .
15.已知函数,其中,若存在
实数b,使得关于x的方程有三个不同的根,则m的
取值范围是______.
16.下列四种说法正确的有 .
①命题“,”的否定是“,使得”;
②若不等式的解集为,则不等式的解集为;
③对于,恒成立,则实数a的取值范围是;
④已知p:,q:,若p是q的充分不必要条件,则实数a的取值范围是.
解答题(本大题共6小题,共70分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
已知函数f(x)=+,M为不等式f(x)<2的解集.
(1)求M;
(2)证明:当a,b∈M时,|a+b|<|1+ab|.
18.(本小题满分12分)
为了了解地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 2015 2016 2017 2018 2019
足球特色学校(百个) 0.30 0.60 1.00 1.40 1.70
(1)根据上表数据,利用与的相关系数,说明与的线性相关性强弱(已知:,则认为与线性相关性很强;,则认为与线性相关性一般;,则认为与线性相关性较弱);
(2)求关于的线性回归方程,并预测地区2020年足球特色学校的个数(精确到个).
本题参考公式和数据:,,
,.
19.(本小题满分12分)
已知函数.
(1)若是定义在R上的偶函数,求实数a的值;
(2)在(1)的条件下,若,求函数的零点.
20.(本小题满分12分)
如图所示,梯形中,,平面平面,且四边形为矩形,,,,.
(1)求证:平面平面;
(2)求直线与平面所成角的正弦值.
(本小题满分12分)
在一个不透明的盒中,装有大小、质地相同的两个小球,其中1个是黑色,1个是白色,甲、乙进行取球游戏,两人随机地从盒中各取一球,两球都取出之后再一起放回盒中,这称为一次取球,约定每次取到白球者得1分,取到黑球者得0分,一人比另一人多3分或取满9次时游戏结束,并且只有当一人比另一人多3分时,得分高者才能获得游戏奖品.已知前3次取球后,甲得2分,乙得1分.
(1)求甲获得游戏奖品的概率;
(2)设表示游戏结束时所进行的取球次数,求的分布列及数学期望.
22.(本小题满分12分)
已知函数g(x)=x2-2ax+1在区间上的值域为.
(1)求a的值;
(2)设函数,
①若不等式在上恒成立,求实数的取值范围;
②若函数有三个零点,求实数的取值范围.
参考答案
1-12:BDCAC CDDBA CB
12.【解析】.故为偶函数,
又结合双勾函数知在上为增函数,在上为减函数,
故在上为增函数.
综上为偶函数,且在上为增函数.
故可得.
解得选B
13.
14.-5
15.
16.②③④
17.(本小题满分10分)
(1)解 f(x)=
当x≤-时,由f(x)<2得-2x<2,
解得x>-1,所以,-1当-当x≥时,由f(x)<2得2x<2,解得x<1,
所以-所以f(x)<2的解集M={x|-1(2)证明 由(1)知,当a,b∈M时,-1从而(a+b)2-(1+ab)2=a2+b2-a2b2-1=(a2-1)(1-b2)<0,即(a+b)2<(1+ab)2,因此|a+b|<|1+ab|.
18.(本小题满分12分)
解:(1),,,
所以,
所以y与线性相关性很强.
(2),,
关于的线性回归方程是.
当时,百个,
即地区2020年足球特色学校有208个.
19.(本小题满分12分)
解:(1)是定义在R上的偶函数.
,即,
故.
函数,
因为.
所以满足题意.
依题意,令,
则有,得,
令,则,
解得.
即.
函数有两个零点,分别为和.
20.(本小题满分12分)
(1)证明:
又平面平面,且平面平面,面
面,又平面平面,
,
在中,,,
在中,,,
,
又,平面,
平面,平面平面;
(2)解:方法一:由(1)可知为直角三角形,且,,
作于,则
由已知平面平面,且平面平面,
面,
面
,
因为,,,所以为等腰三角形
,
设点到平面的距离为,直线与平面所成角为.则
,即,解得:,
又因为,所以.
方法二:空间向量法(略)
21.(本小题满分12分)
解:【解析】(1)设甲获得游戏奖品为事件A:
,
所以甲获得游戏奖品的概率为;
X可能的取值为:5,7,9;
,
的分布列为
5 7 9
的数学期望.
22.(本小题满分12分)
解:在区间上的值域,
若时,的最小值为,
由,可得舍去,
此时满足在区间上的值域;
若时,在递减,的最小值为,
由,解得舍去;
若,则在递增,的最小值为,
由,解得(舍去),
综上可得,;
(2)由已知可得,
①所以在上恒成立可化为,
化为,令,则,因,故,
记,因为,故,
所以的取值范围是.
②由得,
令则有两个不等实根且或
记则
或
两不等式组解集分别为与 的取值范围是.
- 11 -
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合M={x|0
C.充要条件 D.既不充分也不必要条件
2.已知全集为,集合,,则( )
A. B. C. D.
3.已知函数是定义在R上的奇函数,且当时,,则( )
A.2 B.4 C.-2 D.-4
4.设随机变量X~B,则P(X=3)等于( )
A. B. C. D.
5.有下列四个条件:①,,; ②,;③,,; ④、是异面直线,,,。
其中能保证直线//平面的条件是( )
A.①② B.①③ C.①④ D.②④
6. 若且满足,则的最小值是( )
A. B. C.7 D.6
7. 从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件“第一次取到的是奇数”,“第二次取到的是奇数”,则???????
A. B. C. D.
8. 有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 非优秀 总计
甲班 10 b
乙班 c 30
总计
105
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
附:,
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
9. 某学校安排甲、乙、丙、丁四位同学参加数学、物理、化学竞赛,要求每位同学仅报一科,每科至少有一位同学参加,且甲、乙不能参加同一学科,则不同的安排方法有( )
A.36种 B.30种 C.24种 D.6种
某几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
11.已知函数是单调函数,且时,都有,则( ).
A.-4 B.-3 C.-1 D.0
12.设函数,则使得成立的的取值范围是( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
13.如图是具有相关关系的两个变量的一组数据的散点图和回归直
线,若去掉一个点使得余下的个点所对应的数据的相关系数最
大,则应当去掉的点是________.
14.的展开式中x2项的系数为 .
15.已知函数,其中,若存在
实数b,使得关于x的方程有三个不同的根,则m的
取值范围是______.
16.下列四种说法正确的有 .
①命题“,”的否定是“,使得”;
②若不等式的解集为,则不等式的解集为;
③对于,恒成立,则实数a的取值范围是;
④已知p:,q:,若p是q的充分不必要条件,则实数a的取值范围是.
解答题(本大题共6小题,共70分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
已知函数f(x)=+,M为不等式f(x)<2的解集.
(1)求M;
(2)证明:当a,b∈M时,|a+b|<|1+ab|.
18.(本小题满分12分)
为了了解地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 2015 2016 2017 2018 2019
足球特色学校(百个) 0.30 0.60 1.00 1.40 1.70
(1)根据上表数据,利用与的相关系数,说明与的线性相关性强弱(已知:,则认为与线性相关性很强;,则认为与线性相关性一般;,则认为与线性相关性较弱);
(2)求关于的线性回归方程,并预测地区2020年足球特色学校的个数(精确到个).
本题参考公式和数据:,,
,.
19.(本小题满分12分)
已知函数.
(1)若是定义在R上的偶函数,求实数a的值;
(2)在(1)的条件下,若,求函数的零点.
20.(本小题满分12分)
如图所示,梯形中,,平面平面,且四边形为矩形,,,,.
(1)求证:平面平面;
(2)求直线与平面所成角的正弦值.
(本小题满分12分)
在一个不透明的盒中,装有大小、质地相同的两个小球,其中1个是黑色,1个是白色,甲、乙进行取球游戏,两人随机地从盒中各取一球,两球都取出之后再一起放回盒中,这称为一次取球,约定每次取到白球者得1分,取到黑球者得0分,一人比另一人多3分或取满9次时游戏结束,并且只有当一人比另一人多3分时,得分高者才能获得游戏奖品.已知前3次取球后,甲得2分,乙得1分.
(1)求甲获得游戏奖品的概率;
(2)设表示游戏结束时所进行的取球次数,求的分布列及数学期望.
22.(本小题满分12分)
已知函数g(x)=x2-2ax+1在区间上的值域为.
(1)求a的值;
(2)设函数,
①若不等式在上恒成立,求实数的取值范围;
②若函数有三个零点,求实数的取值范围.
参考答案
1-12:BDCAC CDDBA CB
12.【解析】.故为偶函数,
又结合双勾函数知在上为增函数,在上为减函数,
故在上为增函数.
综上为偶函数,且在上为增函数.
故可得.
解得选B
13.
14.-5
15.
16.②③④
17.(本小题满分10分)
(1)解 f(x)=
当x≤-时,由f(x)<2得-2x<2,
解得x>-1,所以,-1
所以-
18.(本小题满分12分)
解:(1),,,
所以,
所以y与线性相关性很强.
(2),,
关于的线性回归方程是.
当时,百个,
即地区2020年足球特色学校有208个.
19.(本小题满分12分)
解:(1)是定义在R上的偶函数.
,即,
故.
函数,
因为.
所以满足题意.
依题意,令,
则有,得,
令,则,
解得.
即.
函数有两个零点,分别为和.
20.(本小题满分12分)
(1)证明:
又平面平面,且平面平面,面
面,又平面平面,
,
在中,,,
在中,,,
,
又,平面,
平面,平面平面;
(2)解:方法一:由(1)可知为直角三角形,且,,
作于,则
由已知平面平面,且平面平面,
面,
面
,
因为,,,所以为等腰三角形
,
设点到平面的距离为,直线与平面所成角为.则
,即,解得:,
又因为,所以.
方法二:空间向量法(略)
21.(本小题满分12分)
解:【解析】(1)设甲获得游戏奖品为事件A:
,
所以甲获得游戏奖品的概率为;
X可能的取值为:5,7,9;
,
的分布列为
5 7 9
的数学期望.
22.(本小题满分12分)
解:在区间上的值域,
若时,的最小值为,
由,可得舍去,
此时满足在区间上的值域;
若时,在递减,的最小值为,
由,解得舍去;
若,则在递增,的最小值为,
由,解得(舍去),
综上可得,;
(2)由已知可得,
①所以在上恒成立可化为,
化为,令,则,因,故,
记,因为,故,
所以的取值范围是.
②由得,
令则有两个不等实根且或
记则
或
两不等式组解集分别为与 的取值范围是.
- 11 -
同课章节目录
