4.2 功率课件 30张PPT
图片预览










文档简介
§4.2 功 率
高中物理(必修二)
感受讨论
A、B两个人从底楼走到二楼,已知每层楼高4米,问:
1、谁克服重力做的功多?
2、谁克服重力做功的快?
谁做的功快?
一头牛一天能耕地五亩田地
一台耕地机一天能耕地约20亩田地
如果让一头牛一天耕20亩地,会出现什么情况?
你想累死
我呀
谁做的功快?
一个农民一天能收割一亩水稻
一部收割机一天能收割数十亩水稻
谁做的功快?
预习填空:
功率:
物理意义: ;
定 义: ;
定 义 式: ;(各物理量的含义还记得吗?)
拓 展 式: ;(功率、力和速度的关系)
功 率 是: (“标量”或“矢量”)
单 位: ;简称: ;符号: ;
1KW= W;
1 W= = (用SI基本单位表示)
描述做功快慢的物理量
功W和完成这些功所用时间t之比
p=
w
t
P=FVcosα
标量
瓦特
瓦
W
1000
1J/s
1kg·m2/s3
比值定义法
还有哪些学过的物理量也是用比值法定义的?
1 马力 ≈ 735 W
说明:
在日常生活中,我们经常说某台机器的功率,或某物体做功的功率,实际上是指某个力对物体做功的功率。例如:汽车的功率就是汽车牵引力的功率,起重机吊起货物的功率就是钢绳拉力的功率。
讨论探究:区分平均功率和瞬时功率
平均功率: ;
瞬时功率: ;
定义式:
P=
t
W
当 t 表示一段时间时,此式表示平均功率
当 t 很短很短时,此式表示瞬时功率
某段时间内机器的功率
某个瞬时(时刻)机器的功率
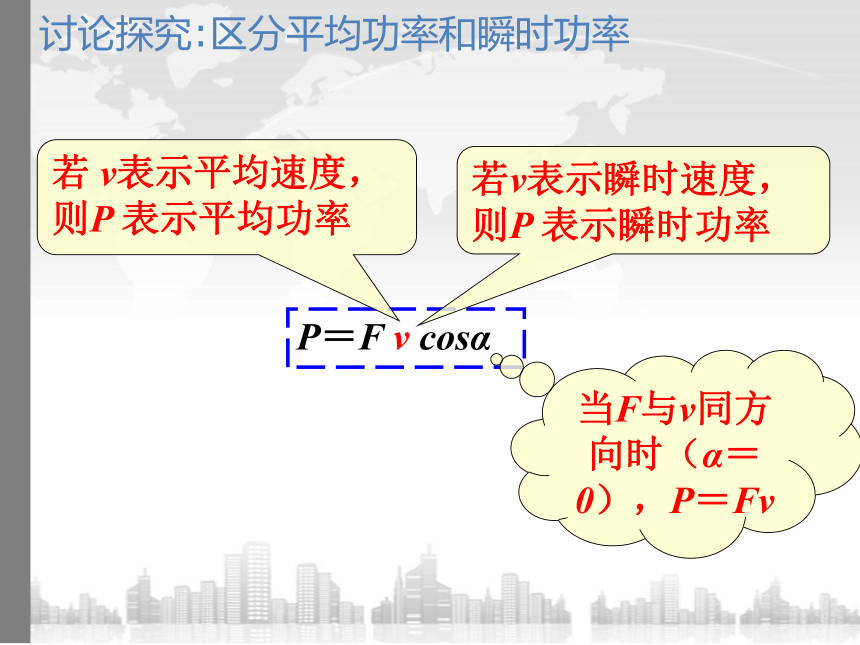
讨论探究:区分平均功率和瞬时功率
P=F v cosα
若 v表示平均速度,则P 表示平均功率
若v表示瞬时速度,则P 表示瞬时功率
当F与v同方向时(α=0),P=Fv
实例分析:P=FV 中三个物理量的决定关系
1.自由下落的物体重力做功的功率;
当F 一定时,P 和 v 有什么关系?
2.水平路面上行驶的汽车,发动机的牵引力;
当P 一定时,F 和 v 有什么关系?
3.汽车匀速爬上坡度越来越陡的山坡;
当v 一定时,F 和 P 有什么关系?
课堂训练
下列说法正确的是( )
A. 做功越多,功率一定越大
B. 做功时间越短,功率一定越大
C.功率是单位时间内完成的功
D.机械效率越大,功率一定越大
C
小资料
长时间运动时人的功率为数10W,优秀运动员可达1kW
长时间运动马的功率为数百瓦
鲸游动时功率可达350kW
小汽车的功率为数十千瓦至两百千瓦
高速列车的功率可达数万kW
万吨豪华游轮的功率可达1万kW以上
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
讨论探究:区分额定功率和实际功率
额定功率: ;
实际功率: ;
机器长时间正常工作允许的功率
机器实际输出的功率
注意:机器不一定在额定功率下工作,机器正常工作时实际功率总是小于或等于额定功率,机器只能在短暂时间内实际功率略大于额定功率,但不允许长时间超过额定功率。
讨论探究
思考:汽车上坡时,司机常会加大油门和降低速度,这样做的目的是什么?
当机械发动机的功率一定时,牵引力与速度成反比,所以可以通过减小速度来增大牵引力。
探究汽车的启动问题
汽车在行驶的过程中,发动机的最大功率等于额定功率。
P = F v
汽车功率
汽车的牵引力
汽车的瞬时速度
汽车加速运动的情况有两种:
1、以额定功率P额启动;
2、在恒定的牵引力F作用下启动。
汽车以恒定功率 P 启动
v
↑
F=
v
P
↓
↑
→
a=
m
F-F阻
→
↓
→
↓
当F=F阻时,
a=0 ,v达到最大
vm=
F阻
P
保持
vm
匀速
加速度逐渐减小的变加速直线运动
匀速直线运动
机车以恒定功率启动的v- t 图
v
t
0
vm
汽车以恒定加速度 a 启动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P=F v
→
↑
↑
当P= P额时,保持P额继续加速
v
↑
F=
v
P额
↑
→
↓
a=
m
F-F阻
→
→
↓
↓
当F= F阻时,
a=0 ,v达到最大
vm=
F阻
P额
保持
vm
匀速
匀加速直线运动
加速度逐渐减小的变加速直线运动
匀速直线运动
汽车以恒定加速度启动的v- t 图
v
t
0
先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
vm
课堂训练
质量m=3kg的物体,在水平力F=6N的作用下,在光滑的水平面上从静止开始运动,运动时间t=3s,求:
(1)力F在t=3s内对物体做的功;
(2)力F在t=3s内对物体做功的平均功率
(3)力F在3s末对物体做功的瞬时功率
要点:
必须弄清是何种类型的功率,并能正确选择公式
(1)由物体的运动的规律,可以求得物体运动的位移的大 小,再根据功的公式可以直接求得功的大小;
(2)求的是平均功率,用前面求出的总功除以总的时间就 可以;
(3)瞬时功率要用力与瞬时速度的乘积来计算,根据运动 规律可以求得瞬时速度的大小,再由瞬时功率的公式可以求得瞬时功率的大小.
36W
18W
54J
解:(1)物体做匀加速直线运动,由牛顿第二定律可得
a=F/m =6/3 m/s2=2m/s2,
3s物体运动的位移是 x=at2/2=9m,
力F在3s内对物体所做的功为 W=Fx=6×9J=54J.
(2)力F在3s内对物体所做的功的平均功率为
P =W/t =54/3 W=18W
(3)3s末物体的速度为 v=at=6m/s
所以3s末力F对物体所做的功的瞬时功率为,
P=Fv=6×6W=36W
答:(1)力F在3s内对物体所做的功是54J;
(2)力F在3s内对物体所做的功的平均功率是18W;
(3)3s末力F对物体所做的功的瞬时功率是36W.
科学家介绍:
今天你学到了什么?
1、物理意义:表示做功快慢的物理量
2、定义式:
P=
t
W
该式一般用于求平均功率
3、计算式:P = F v cosα
该式用于求瞬时功率、平均功率
4、单位:在国际单位制中 瓦特 W
思考与讨论:
怎样估测出自己在一项体育运动中的功率?
高中物理(必修二)
感受讨论
A、B两个人从底楼走到二楼,已知每层楼高4米,问:
1、谁克服重力做的功多?
2、谁克服重力做功的快?
谁做的功快?
一头牛一天能耕地五亩田地
一台耕地机一天能耕地约20亩田地
如果让一头牛一天耕20亩地,会出现什么情况?
你想累死
我呀
谁做的功快?
一个农民一天能收割一亩水稻
一部收割机一天能收割数十亩水稻
谁做的功快?
预习填空:
功率:
物理意义: ;
定 义: ;
定 义 式: ;(各物理量的含义还记得吗?)
拓 展 式: ;(功率、力和速度的关系)
功 率 是: (“标量”或“矢量”)
单 位: ;简称: ;符号: ;
1KW= W;
1 W= = (用SI基本单位表示)
描述做功快慢的物理量
功W和完成这些功所用时间t之比
p=
w
t
P=FVcosα
标量
瓦特
瓦
W
1000
1J/s
1kg·m2/s3
比值定义法
还有哪些学过的物理量也是用比值法定义的?
1 马力 ≈ 735 W
说明:
在日常生活中,我们经常说某台机器的功率,或某物体做功的功率,实际上是指某个力对物体做功的功率。例如:汽车的功率就是汽车牵引力的功率,起重机吊起货物的功率就是钢绳拉力的功率。
讨论探究:区分平均功率和瞬时功率
平均功率: ;
瞬时功率: ;
定义式:
P=
t
W
当 t 表示一段时间时,此式表示平均功率
当 t 很短很短时,此式表示瞬时功率
某段时间内机器的功率
某个瞬时(时刻)机器的功率
讨论探究:区分平均功率和瞬时功率
P=F v cosα
若 v表示平均速度,则P 表示平均功率
若v表示瞬时速度,则P 表示瞬时功率
当F与v同方向时(α=0),P=Fv
实例分析:P=FV 中三个物理量的决定关系
1.自由下落的物体重力做功的功率;
当F 一定时,P 和 v 有什么关系?
2.水平路面上行驶的汽车,发动机的牵引力;
当P 一定时,F 和 v 有什么关系?
3.汽车匀速爬上坡度越来越陡的山坡;
当v 一定时,F 和 P 有什么关系?
课堂训练
下列说法正确的是( )
A. 做功越多,功率一定越大
B. 做功时间越短,功率一定越大
C.功率是单位时间内完成的功
D.机械效率越大,功率一定越大
C
小资料
长时间运动时人的功率为数10W,优秀运动员可达1kW
长时间运动马的功率为数百瓦
鲸游动时功率可达350kW
小汽车的功率为数十千瓦至两百千瓦
高速列车的功率可达数万kW
万吨豪华游轮的功率可达1万kW以上
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
机械铭牌标明机器的功率
讨论探究:区分额定功率和实际功率
额定功率: ;
实际功率: ;
机器长时间正常工作允许的功率
机器实际输出的功率
注意:机器不一定在额定功率下工作,机器正常工作时实际功率总是小于或等于额定功率,机器只能在短暂时间内实际功率略大于额定功率,但不允许长时间超过额定功率。
讨论探究
思考:汽车上坡时,司机常会加大油门和降低速度,这样做的目的是什么?
当机械发动机的功率一定时,牵引力与速度成反比,所以可以通过减小速度来增大牵引力。
探究汽车的启动问题
汽车在行驶的过程中,发动机的最大功率等于额定功率。
P = F v
汽车功率
汽车的牵引力
汽车的瞬时速度
汽车加速运动的情况有两种:
1、以额定功率P额启动;
2、在恒定的牵引力F作用下启动。
汽车以恒定功率 P 启动
v
↑
F=
v
P
↓
↑
→
a=
m
F-F阻
→
↓
→
↓
当F=F阻时,
a=0 ,v达到最大
vm=
F阻
P
保持
vm
匀速
加速度逐渐减小的变加速直线运动
匀速直线运动
机车以恒定功率启动的v- t 图
v
t
0
vm
汽车以恒定加速度 a 启动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P=F v
→
↑
↑
当P= P额时,保持P额继续加速
v
↑
F=
v
P额
↑
→
↓
a=
m
F-F阻
→
→
↓
↓
当F= F阻时,
a=0 ,v达到最大
vm=
F阻
P额
保持
vm
匀速
匀加速直线运动
加速度逐渐减小的变加速直线运动
匀速直线运动
汽车以恒定加速度启动的v- t 图
v
t
0
先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
vm
课堂训练
质量m=3kg的物体,在水平力F=6N的作用下,在光滑的水平面上从静止开始运动,运动时间t=3s,求:
(1)力F在t=3s内对物体做的功;
(2)力F在t=3s内对物体做功的平均功率
(3)力F在3s末对物体做功的瞬时功率
要点:
必须弄清是何种类型的功率,并能正确选择公式
(1)由物体的运动的规律,可以求得物体运动的位移的大 小,再根据功的公式可以直接求得功的大小;
(2)求的是平均功率,用前面求出的总功除以总的时间就 可以;
(3)瞬时功率要用力与瞬时速度的乘积来计算,根据运动 规律可以求得瞬时速度的大小,再由瞬时功率的公式可以求得瞬时功率的大小.
36W
18W
54J
解:(1)物体做匀加速直线运动,由牛顿第二定律可得
a=F/m =6/3 m/s2=2m/s2,
3s物体运动的位移是 x=at2/2=9m,
力F在3s内对物体所做的功为 W=Fx=6×9J=54J.
(2)力F在3s内对物体所做的功的平均功率为
P =W/t =54/3 W=18W
(3)3s末物体的速度为 v=at=6m/s
所以3s末力F对物体所做的功的瞬时功率为,
P=Fv=6×6W=36W
答:(1)力F在3s内对物体所做的功是54J;
(2)力F在3s内对物体所做的功的平均功率是18W;
(3)3s末力F对物体所做的功的瞬时功率是36W.
科学家介绍:
今天你学到了什么?
1、物理意义:表示做功快慢的物理量
2、定义式:
P=
t
W
该式一般用于求平均功率
3、计算式:P = F v cosα
该式用于求瞬时功率、平均功率
4、单位:在国际单位制中 瓦特 W
思考与讨论:
怎样估测出自己在一项体育运动中的功率?
