7.5.2 三角形内角和定理 课件(共25张PPT)
文档属性
| 名称 | 7.5.2 三角形内角和定理 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 19:19:31 | ||
图片预览





文档简介
数学北师大版
八年级上
7.5 三角形内角和定理(二)
把△ABC的内角∠ACB的一边BC延长得到∠ACD,
这个角叫做△ABC的外角
A
B
C
D
三角形的一边与另一边的反向延长线所组成的角,叫做三角形的外角.
三角形一共有6个外角
三角形一个顶点处有2个外角
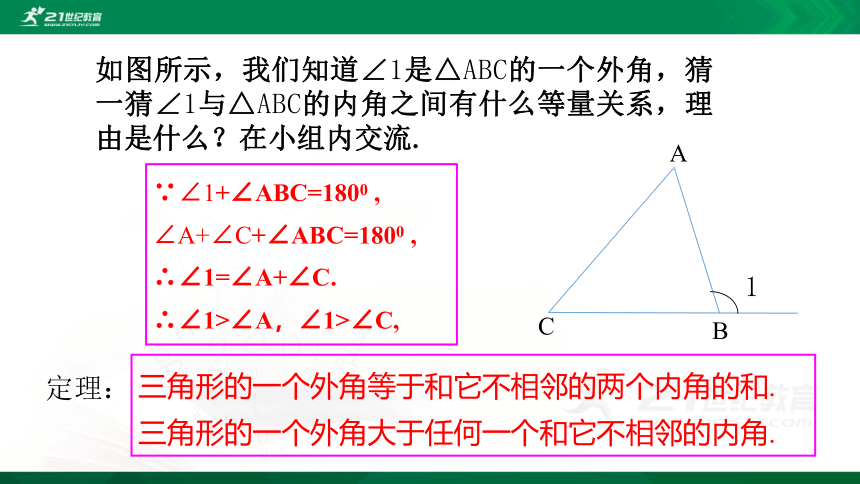
如图所示,我们知道∠1是△ABC的一个外角,猜一猜∠1与△ABC的内角之间有什么等量关系,理由是什么?在小组内交流.
A
C
B
1
∵∠1+∠ABC=1800 ,
∠A+∠C+∠ABC=1800 ,
∴∠1=∠A+∠C.
∴∠1>∠A,∠1>∠C,
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
定理:
∴∠B= ∠EAC.
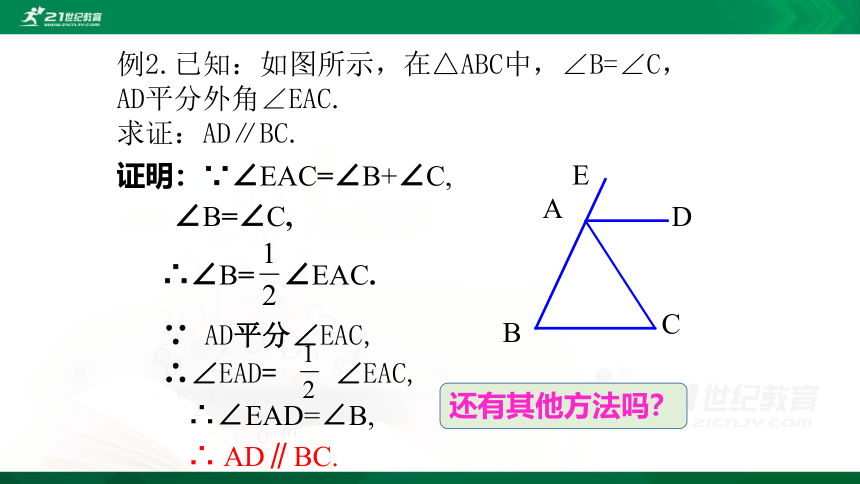
例2.已知:如图所示,在△ABC中,∠B=∠C,AD平分外角∠EAC.
求证:AD∥BC.
证明:∵∠EAC=∠B+∠C,
∠B=∠C,
∴∠EAD=∠B,
∴ AD∥BC.
A
C
D
B
E
∵ AD平分∠EAC,
∴∠EAD= ∠EAC,
还有其他方法吗?
练习:如图是由线段AB,CD,DF,BF ,CA组成的平面图形,∠D= 28°,则∠A十∠B十∠C+∠F的度数为多少?
解:∠A+∠C=∠DGA
∠B+∠F=∠BED
①
②
①+②
∠A十∠B十∠C+∠F
=∠DGA+∠BED
=180°-∠DGE+180°-∠GED
=360°-(∠DGE+∠GED)
=360°-(180°-∠D)
=360°-180°+∠D=180°+∠D
如图
∠A+∠B+∠C+∠D+∠E的度数为多少?
解:在ΔEFG中
∠E十∠EFG十∠EGF=180°
思考:∠EFG是哪一个三角形的外角?
找出组成∠EFG的二条直线,
用一边的反向线与另一边组成的三角形是FBD。
故∠EFG是三角形FBD的外角
又∠EFG=∠B+D
思考:∠EGF是哪一个三角形的外角?
找出组成∠EGF的二条直线,
用一边的反向线与另一边组成的三角形是GAC。
故∠EGF是三角形GAC的外角
∠EGF=∠A+C
∴∠E十∠B十∠D十∠A十∠C=180°
∴∠A+∠B+∠C+∠D+∠E=180°
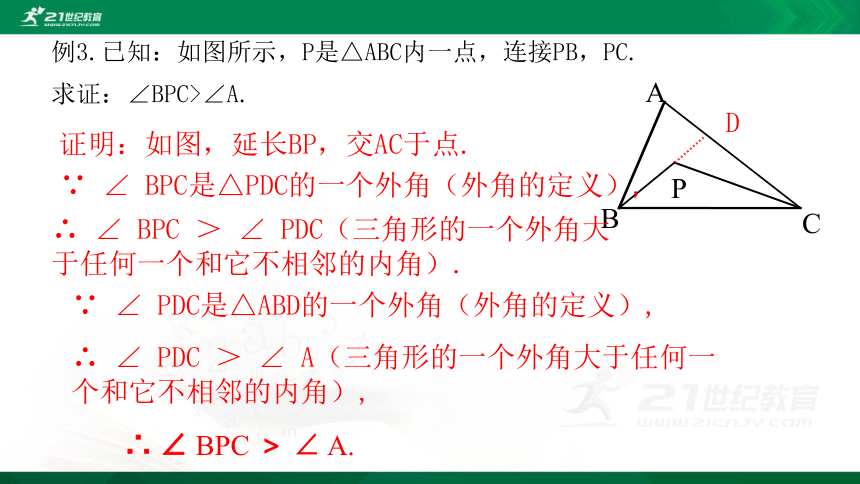
例3.已知:如图所示,P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
A
B
C
P
证明:如图,延长BP,交AC于点.
∵ ∠ BPC是△PDC的一个外角(外角的定义),
∴ ∠ BPC > ∠ PDC(三角形的一个外角大于任何一个和它不相邻的内角).
∵ ∠ PDC是△ABD的一个外角(外角的定义),
∴ ∠ PDC > ∠ A(三角形的一个外角大于任何一个和它不相邻的内角),
∴ ∠ BPC > ∠ A.
D
A
B
C
P
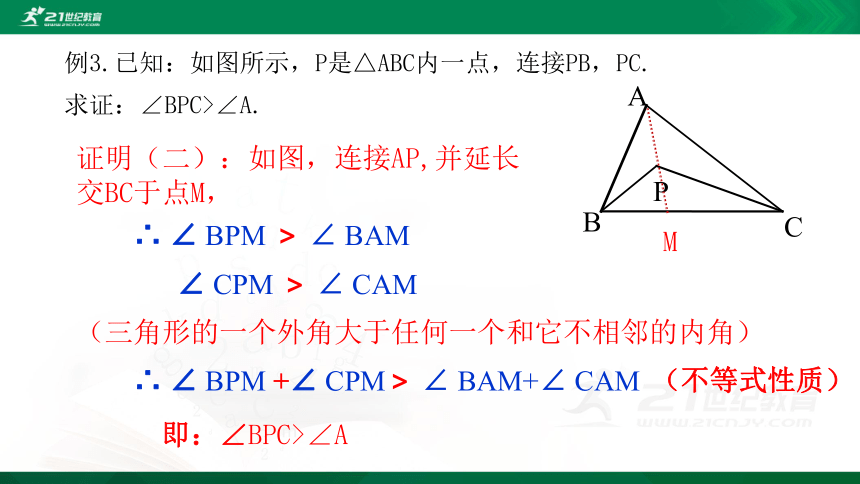
例3.已知:如图所示,P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
证明(二):如图,连接AP,并延长交BC于点M,
M
∴ ∠ BPM > ∠ BAM
∠ CPM > ∠ CAM
∴ ∠ BPM +∠ CPM> ∠ BAM+∠ CAM
即:∠BPC>∠A
(三角形的一个外角大于任何一个和它不相邻的内角)
(不等式性质)
课后作业如下
1. 如图,在△ABC中,∠A=40°,∠B=72°,CD是AB边上的高,CE是∠ACB的平分线,DF⊥CE于F,求∠CDF的度数.
解:∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣40°﹣72°=68°
∵CE是∠ACB的平分线,
∴∠BCE= ∠ACB= ×68°=34°
∵CD⊥AB即∠CDB=90°,
∴∠BCD=180°﹣90°﹣72°=18°,
∴∠DCE=∠BCE﹣∠BCD=34°﹣18°=16°.
∵DF⊥CE即∠DFC=90°,
∴∠CDF=180°﹣90°﹣16°=74°.
2.如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC于D,AE平分∠BAC,求∠DAE的度数.
解:在△ABC中,
∵∠BAC+∠B+∠ACB=180°,∠B=24°,∠ACB=104°,
∴∠BAC=180°﹣∠B﹣∠ACB
=180°﹣24°﹣104°=52°
∵AE平分∠BAC,
∴∠EAC= ∠BAC= ×52°=26°,
∵AD⊥BC,∴∠ADC=90°,
∵∠ACB=104°,
∴∠ACD=180°﹣∠ACB
=180°﹣104°=76°,
∴∠CAD=14°,
∴∠DAE=∠EAC+∠CAD=40°.
3.如图,CE是△ABC的外角∠ACF的平分线,CE交BA的延长线于点E,则∠BAC与∠B谁大?并说明理由.
解:∠BAC>∠B,
∵∠BAC是△ACE的外角,
∴∠BAC>∠1,
∵CE是△ABC的外角∠ACF的平分线,
∴∠BAC>∠2,
∴∠2>∠B,
∴∠1=∠2,
∵∠2是△BCE的外角,
∴∠BAC>∠B.
4.如图:CE是△ABC外角∠ACD的角平分线,CE交BA于E.求证:∠BAC>∠B.
证明:∵EC是∠ACD的平分线,
∴∠ACE=∠ECD,
∵∠ECD=∠B+∠E,
∴∠ECD>∠B,
而∠BAC=∠E+∠ECA,
∴∠BAC>∠B.
5.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC等于( )
A.42° B.66°
C.69° D.77°
C
巩固提高
6.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80°
C.75° D.70°
7.如图,在△ABC中,∠A=50°,∠ABC、∠ACB的
角平分线相交于点P,
则∠BPC的度数为 .
A
115°
巩固提高
8.如图,把三角形ABC纸片沿DE折叠,使点A落在四边形BCED的内部,已知∠1+∠2=80°,则∠A的度数为 .
40°
巩固提高
9.如图:∠A=65°,∠ABD=∠DCE=30°,且CE平分∠ACB,求∠BEC的度数.
解:∵∠A=65°,∠ABD=30°,
∴∠BDC=∠A+∠ABD
=65°+30°=95°,
∴∠BEC=∠EDC+∠DCE
=95°+30°=125°.
10.如图,在△ABC中,∠B=∠C,AD平分外角∠EAC,说明AD∥BC.
证明:∵AD平分∠EAC,
∴∠EAD= ∠EAC.
又∵∠B=∠C,∠EAC=∠B+∠C,
∴∠B= ∠EAC.
∴∠EAD=∠B.
所以AD∥BC.
11.如图, MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
解:延长MF交CD于点H,
∵∠1=90°+∠CFH,∠1=140°,∠2=50°,
∴∠CHF=140°﹣90°=50°,
∴∠CHF=∠2,
∴AB∥CD.
巩固提高
12.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.若∠B=35°,∠E=20°,求∠BAC的度数.
解:∵∠B=35°,∠E=20°,
∴∠ECD=∠B+∠E=55°,
∵CE是△ABC的外角∠ACD的平分线,
∴∠ACD=2∠ECD=110°,
∴∠BAC=∠ACD﹣∠B=75°.
13. 一个零件的形状如图所示,按规定∠A=90°,∠B和∠C应分别是32°和21°,检验工人量得∠BDC=148°,就断定这个零件不合格,请运用三角形的有关知识说明零件不合格的理由.
解:延长CD交AB于点E,
∵∠BDC是△DBE的一个外角,
∴∠BDC=∠B+∠DEB.
∵∠DEB是△AEC的一个外角,
∴∠DEB=∠C+∠A
即∠BDC=∠C+∠B+∠A=21°+32°+90°=143°,
而测量的结果是∠BDC=148°,
∴零件不合格
E
14.如图,在△ABC中,∠B= 90°,∠_ACB、∠CAF的平分线所在的直线交于点H,求∠H的度数.
解:∵ CH、AD分别为∠ACB、∠CAF的平分线,
∠H= ∠CAD-∠ACH
= ∠CAF- ∠ACB
(三角形的一个外角等于与它不相邻的两个内角的和),
= (180°-∠BAC)- ∠ACB
=90°- ∠BAC- ∠ACB
=90°- (∠BAC+∠ACB)
=45°
=90°- ×90°
∠A1=180-∠ABC-∠A1CB
=180°- ∠ABC-(∠A1CA+∠ACB)
=180°- ∠ABC-∠A1CA-∠ACB
=180°- ∠ABC- (180°- ∠ACB) - ∠ACB
=180°- ∠ABC- ∠ACB
=180°- (∠ABC+∠ACB)
=180°- (180°- α)= α
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级上
7.5 三角形内角和定理(二)
把△ABC的内角∠ACB的一边BC延长得到∠ACD,
这个角叫做△ABC的外角
A
B
C
D
三角形的一边与另一边的反向延长线所组成的角,叫做三角形的外角.
三角形一共有6个外角
三角形一个顶点处有2个外角
如图所示,我们知道∠1是△ABC的一个外角,猜一猜∠1与△ABC的内角之间有什么等量关系,理由是什么?在小组内交流.
A
C
B
1
∵∠1+∠ABC=1800 ,
∠A+∠C+∠ABC=1800 ,
∴∠1=∠A+∠C.
∴∠1>∠A,∠1>∠C,
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
定理:
∴∠B= ∠EAC.
例2.已知:如图所示,在△ABC中,∠B=∠C,AD平分外角∠EAC.
求证:AD∥BC.
证明:∵∠EAC=∠B+∠C,
∠B=∠C,
∴∠EAD=∠B,
∴ AD∥BC.
A
C
D
B
E
∵ AD平分∠EAC,
∴∠EAD= ∠EAC,
还有其他方法吗?
练习:如图是由线段AB,CD,DF,BF ,CA组成的平面图形,∠D= 28°,则∠A十∠B十∠C+∠F的度数为多少?
解:∠A+∠C=∠DGA
∠B+∠F=∠BED
①
②
①+②
∠A十∠B十∠C+∠F
=∠DGA+∠BED
=180°-∠DGE+180°-∠GED
=360°-(∠DGE+∠GED)
=360°-(180°-∠D)
=360°-180°+∠D=180°+∠D
如图
∠A+∠B+∠C+∠D+∠E的度数为多少?
解:在ΔEFG中
∠E十∠EFG十∠EGF=180°
思考:∠EFG是哪一个三角形的外角?
找出组成∠EFG的二条直线,
用一边的反向线与另一边组成的三角形是FBD。
故∠EFG是三角形FBD的外角
又∠EFG=∠B+D
思考:∠EGF是哪一个三角形的外角?
找出组成∠EGF的二条直线,
用一边的反向线与另一边组成的三角形是GAC。
故∠EGF是三角形GAC的外角
∠EGF=∠A+C
∴∠E十∠B十∠D十∠A十∠C=180°
∴∠A+∠B+∠C+∠D+∠E=180°
例3.已知:如图所示,P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
A
B
C
P
证明:如图,延长BP,交AC于点.
∵ ∠ BPC是△PDC的一个外角(外角的定义),
∴ ∠ BPC > ∠ PDC(三角形的一个外角大于任何一个和它不相邻的内角).
∵ ∠ PDC是△ABD的一个外角(外角的定义),
∴ ∠ PDC > ∠ A(三角形的一个外角大于任何一个和它不相邻的内角),
∴ ∠ BPC > ∠ A.
D
A
B
C
P
例3.已知:如图所示,P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
证明(二):如图,连接AP,并延长交BC于点M,
M
∴ ∠ BPM > ∠ BAM
∠ CPM > ∠ CAM
∴ ∠ BPM +∠ CPM> ∠ BAM+∠ CAM
即:∠BPC>∠A
(三角形的一个外角大于任何一个和它不相邻的内角)
(不等式性质)
课后作业如下
1. 如图,在△ABC中,∠A=40°,∠B=72°,CD是AB边上的高,CE是∠ACB的平分线,DF⊥CE于F,求∠CDF的度数.
解:∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣40°﹣72°=68°
∵CE是∠ACB的平分线,
∴∠BCE= ∠ACB= ×68°=34°
∵CD⊥AB即∠CDB=90°,
∴∠BCD=180°﹣90°﹣72°=18°,
∴∠DCE=∠BCE﹣∠BCD=34°﹣18°=16°.
∵DF⊥CE即∠DFC=90°,
∴∠CDF=180°﹣90°﹣16°=74°.
2.如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC于D,AE平分∠BAC,求∠DAE的度数.
解:在△ABC中,
∵∠BAC+∠B+∠ACB=180°,∠B=24°,∠ACB=104°,
∴∠BAC=180°﹣∠B﹣∠ACB
=180°﹣24°﹣104°=52°
∵AE平分∠BAC,
∴∠EAC= ∠BAC= ×52°=26°,
∵AD⊥BC,∴∠ADC=90°,
∵∠ACB=104°,
∴∠ACD=180°﹣∠ACB
=180°﹣104°=76°,
∴∠CAD=14°,
∴∠DAE=∠EAC+∠CAD=40°.
3.如图,CE是△ABC的外角∠ACF的平分线,CE交BA的延长线于点E,则∠BAC与∠B谁大?并说明理由.
解:∠BAC>∠B,
∵∠BAC是△ACE的外角,
∴∠BAC>∠1,
∵CE是△ABC的外角∠ACF的平分线,
∴∠BAC>∠2,
∴∠2>∠B,
∴∠1=∠2,
∵∠2是△BCE的外角,
∴∠BAC>∠B.
4.如图:CE是△ABC外角∠ACD的角平分线,CE交BA于E.求证:∠BAC>∠B.
证明:∵EC是∠ACD的平分线,
∴∠ACE=∠ECD,
∵∠ECD=∠B+∠E,
∴∠ECD>∠B,
而∠BAC=∠E+∠ECA,
∴∠BAC>∠B.
5.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC等于( )
A.42° B.66°
C.69° D.77°
C
巩固提高
6.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80°
C.75° D.70°
7.如图,在△ABC中,∠A=50°,∠ABC、∠ACB的
角平分线相交于点P,
则∠BPC的度数为 .
A
115°
巩固提高
8.如图,把三角形ABC纸片沿DE折叠,使点A落在四边形BCED的内部,已知∠1+∠2=80°,则∠A的度数为 .
40°
巩固提高
9.如图:∠A=65°,∠ABD=∠DCE=30°,且CE平分∠ACB,求∠BEC的度数.
解:∵∠A=65°,∠ABD=30°,
∴∠BDC=∠A+∠ABD
=65°+30°=95°,
∴∠BEC=∠EDC+∠DCE
=95°+30°=125°.
10.如图,在△ABC中,∠B=∠C,AD平分外角∠EAC,说明AD∥BC.
证明:∵AD平分∠EAC,
∴∠EAD= ∠EAC.
又∵∠B=∠C,∠EAC=∠B+∠C,
∴∠B= ∠EAC.
∴∠EAD=∠B.
所以AD∥BC.
11.如图, MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
解:延长MF交CD于点H,
∵∠1=90°+∠CFH,∠1=140°,∠2=50°,
∴∠CHF=140°﹣90°=50°,
∴∠CHF=∠2,
∴AB∥CD.
巩固提高
12.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.若∠B=35°,∠E=20°,求∠BAC的度数.
解:∵∠B=35°,∠E=20°,
∴∠ECD=∠B+∠E=55°,
∵CE是△ABC的外角∠ACD的平分线,
∴∠ACD=2∠ECD=110°,
∴∠BAC=∠ACD﹣∠B=75°.
13. 一个零件的形状如图所示,按规定∠A=90°,∠B和∠C应分别是32°和21°,检验工人量得∠BDC=148°,就断定这个零件不合格,请运用三角形的有关知识说明零件不合格的理由.
解:延长CD交AB于点E,
∵∠BDC是△DBE的一个外角,
∴∠BDC=∠B+∠DEB.
∵∠DEB是△AEC的一个外角,
∴∠DEB=∠C+∠A
即∠BDC=∠C+∠B+∠A=21°+32°+90°=143°,
而测量的结果是∠BDC=148°,
∴零件不合格
E
14.如图,在△ABC中,∠B= 90°,∠_ACB、∠CAF的平分线所在的直线交于点H,求∠H的度数.
解:∵ CH、AD分别为∠ACB、∠CAF的平分线,
∠H= ∠CAD-∠ACH
= ∠CAF- ∠ACB
(三角形的一个外角等于与它不相邻的两个内角的和),
= (180°-∠BAC)- ∠ACB
=90°- ∠BAC- ∠ACB
=90°- (∠BAC+∠ACB)
=45°
=90°- ×90°
∠A1=180-∠ABC-∠A1CB
=180°- ∠ABC-(∠A1CA+∠ACB)
=180°- ∠ABC-∠A1CA-∠ACB
=180°- ∠ABC- (180°- ∠ACB) - ∠ACB
=180°- ∠ABC- ∠ACB
=180°- (∠ABC+∠ACB)
=180°- (180°- α)= α
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
