7.5.1 三角形内角和定理 课件(共16张PPT)
文档属性
| 名称 | 7.5.1 三角形内角和定理 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 00:00:00 | ||
图片预览






文档简介
数学北师大版
八年级上
7.5 三角形内角和定理(一)
三角形的内角和定理:三角形的内角和是180°
已知:如图,△ABC
求证:∠A+∠B+∠C=180°
A
B
C
证明:延长BC到D,
则 ∠1= ∠A (两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
∵ ∠1+ ∠2+ ∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠C=180°
过点C作射线CE∥BA,
1
?2
?
A
B
C
已知:如图,△ABC
求证:∠A+∠B+∠C=180°
另种证法
证明:过C作AB的平行线EF,即EF∥AB,则 ∠ACE=∠A(两直线平行,内错角相等)
∠BCF= ∠B(两直线平行,内错角相等)
又∵∠ACE+∠BCF+∠ACB=1800 (平角的定义)
∴ ∠A+∠B+∠ACB=1800 (等量代换)
E
F
证明:过点C作CE∥AB,则
∠ACE=∠A(两直线平行,内错角相等)
∠B+∠BCE=180°(两直线平行,同旁内角互补)
即∠B+∠BCA+∠ACE=180°
∴ ∠B+∠BCA+∠A=180° (等量代换)
A
B
C
E
说明:为了证明三个角的和为180°,把问题转化
为互补的两个角求解;
已知:如图,△ABC
求证:∠A+∠B+∠C=180°
证法三
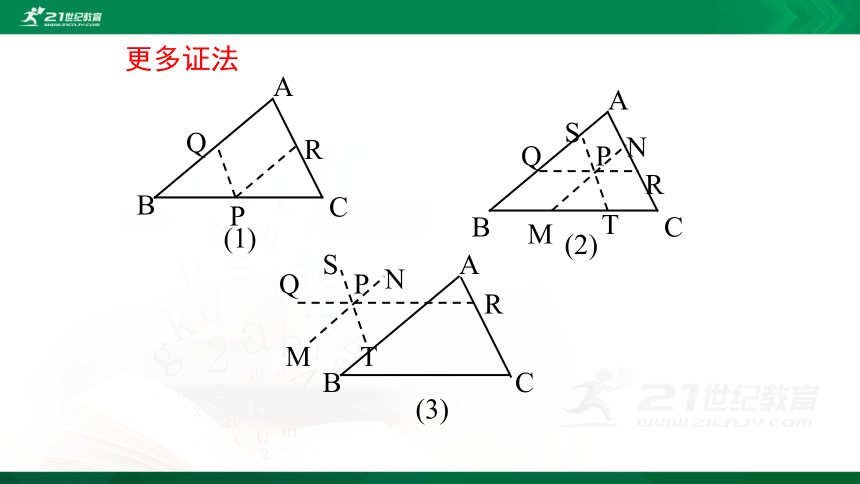
(1)
A
B
C
P
Q
R
T
S
N
(3)
A
B
C
P
Q
R
M
T
S
N
(2)
A
B
C
P
Q
R
M
更多证法
A
B
C
∠A+∠B+∠C=180°
∠A=180°-∠B-∠C=180°-(∠B+∠C)
∠A+∠B=180°-∠C
三角形的内角和是180°可以写成下列各式
任意一个角等于180°减去另外二个角,或
减去另外二个角的和,
任意二个角的和等于180°减去另外一个角
例;如图,在△ABC中,∠B=38°, ∠C=62°AD是△ABC的角平分线,
求∠ADB的度数。
解: 在△ABC中,
∠B+ ∠C+ ∠BAC=180°(三角形内角和定理)
∵ ∠B=38°,∠C=62°(已知)
∴ ∠BAC=180°- 38°-62°= 80°(等式的性质)
∵ AD平分∠BAC(已知)
∴ ∠BAD= ∠CAD = (角平分线的定义)
∠B+ ∠BAD+ ∠ADB=180°(三角形内角和定理)
∵ ∠B=38°(已知),∠BAD=40°(已证)
∴ ∠ADB= 180°- 38°-40°= 102°
练习:如图,在△ABC中,∠A=60°,
∠C=70°D,E分 别是AB,AC上
的点,且DE∥BC,求∠ADE的度数。
解: 在△ABC中,
∠B+∠C+∠BAC=180°
∵ ∠A=60°,∠C=70°
∴ ∠B=180°- 60°-70°= 50°
∵ DE∥BC
∴∠ADE=∠B= 50°
解:
∴ ∠ABC+∠ACB=180°-∠A(等式的性质)
又∵BE、CF分别平分∠ABC 和∠ACB(已知)
∴ ∠BOC=180° -(∠1+∠2)=180° -(90°- ɑ) =90°+ ɑ
∵∠A+∠ABC+∠ACB=1800 (三角形的内角和定理)
∴ ∠ABC+∠ACB=180°-ɑ (等量代换)
∴ ∠1= ∠ABC ,∠2= ∠ACB(角平分线的定义)
∴∠1+∠2= (∠ABC+∠ACB)= ×(180°-ɑ )=90°- ɑ
又∵∠BOC+∠1+∠2=180° (三角形的内角和定理)
A
B
C
E
F
O
1
2
例:如图,已知△ABC中,∠A=α ,∠ABC 和∠ACB的平分线BE、CF交于点O.求∠BOC
练习:如图,已知△ABC中,∠A=50°,∠ABC 和∠ACB的平分线BE、CF交于点O.求∠BOC
解:
∴ ∠ABC+∠ACB=180°-∠A(等式的性质)
又∵BE、CF分别平分∠ABC 和∠ACB(已知)
∴ ∠BOC=180°-(∠1+∠2)=180°-65°=115°(等式的性质)
∵∠A+∠ABC+∠ACB=180° (三角形的内角和定理)
∴ ∠ABC+∠ACB=180°-50°=130°(等量代换)
∴ ∠1= ∠ABC ∠2= ∠ACB(角平分线的定义)
∴∠1+∠2= (∠ABC+∠ACB)= ×130°=65°(等式的性质)
又∵∠BOC+∠1+∠2=180° (三角形的内角和定理)
A
B
C
E
F
O
1
2
课后作业
习题7.6 1,2.3,4
1.如图,已知∠B= 35° ,∠C=60°,
AD⊥BC,AE平分∠BAC,求∠EAD的度数.
解:在△ABC中,
∠BAC= 180°-B-∠C= 85°,
∵AD⊥ BC
∴∠ADE= 90°
∵AE平分∠BAC,
选做题:
2.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠DAC= 26° ,∠CBE=22°.求∠BAC的度数.
3.在△ABC中,∠B= 90°,AD平分∠CAE,CD平分∠ACF,AD、CD相交于点D.求∠D的度数 .
证明:在△ABC中,
∵∠B= 90°
∴∠BAC+∠BCA = 90°.
∵AD平分∠CAE,CD平分∠ACF.
∴∠DAC= ∠EAC
∠DCA= ∠FCA
= ( 180°-∠BAC)
= ( 180°-∠CBA)
∴∠DAC+∠DCA=
( 180°-∠BAC)+
( 180°-∠CBA)
=180°- (∠BAC+∠CBA)
=180°-45°=135°
∴∠D=
180°-135°=45°
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级上
7.5 三角形内角和定理(一)
三角形的内角和定理:三角形的内角和是180°
已知:如图,△ABC
求证:∠A+∠B+∠C=180°
A
B
C
证明:延长BC到D,
则 ∠1= ∠A (两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
∵ ∠1+ ∠2+ ∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠C=180°
过点C作射线CE∥BA,
1
?2
?
A
B
C
已知:如图,△ABC
求证:∠A+∠B+∠C=180°
另种证法
证明:过C作AB的平行线EF,即EF∥AB,则 ∠ACE=∠A(两直线平行,内错角相等)
∠BCF= ∠B(两直线平行,内错角相等)
又∵∠ACE+∠BCF+∠ACB=1800 (平角的定义)
∴ ∠A+∠B+∠ACB=1800 (等量代换)
E
F
证明:过点C作CE∥AB,则
∠ACE=∠A(两直线平行,内错角相等)
∠B+∠BCE=180°(两直线平行,同旁内角互补)
即∠B+∠BCA+∠ACE=180°
∴ ∠B+∠BCA+∠A=180° (等量代换)
A
B
C
E
说明:为了证明三个角的和为180°,把问题转化
为互补的两个角求解;
已知:如图,△ABC
求证:∠A+∠B+∠C=180°
证法三
(1)
A
B
C
P
Q
R
T
S
N
(3)
A
B
C
P
Q
R
M
T
S
N
(2)
A
B
C
P
Q
R
M
更多证法
A
B
C
∠A+∠B+∠C=180°
∠A=180°-∠B-∠C=180°-(∠B+∠C)
∠A+∠B=180°-∠C
三角形的内角和是180°可以写成下列各式
任意一个角等于180°减去另外二个角,或
减去另外二个角的和,
任意二个角的和等于180°减去另外一个角
例;如图,在△ABC中,∠B=38°, ∠C=62°AD是△ABC的角平分线,
求∠ADB的度数。
解: 在△ABC中,
∠B+ ∠C+ ∠BAC=180°(三角形内角和定理)
∵ ∠B=38°,∠C=62°(已知)
∴ ∠BAC=180°- 38°-62°= 80°(等式的性质)
∵ AD平分∠BAC(已知)
∴ ∠BAD= ∠CAD = (角平分线的定义)
∠B+ ∠BAD+ ∠ADB=180°(三角形内角和定理)
∵ ∠B=38°(已知),∠BAD=40°(已证)
∴ ∠ADB= 180°- 38°-40°= 102°
练习:如图,在△ABC中,∠A=60°,
∠C=70°D,E分 别是AB,AC上
的点,且DE∥BC,求∠ADE的度数。
解: 在△ABC中,
∠B+∠C+∠BAC=180°
∵ ∠A=60°,∠C=70°
∴ ∠B=180°- 60°-70°= 50°
∵ DE∥BC
∴∠ADE=∠B= 50°
解:
∴ ∠ABC+∠ACB=180°-∠A(等式的性质)
又∵BE、CF分别平分∠ABC 和∠ACB(已知)
∴ ∠BOC=180° -(∠1+∠2)=180° -(90°- ɑ) =90°+ ɑ
∵∠A+∠ABC+∠ACB=1800 (三角形的内角和定理)
∴ ∠ABC+∠ACB=180°-ɑ (等量代换)
∴ ∠1= ∠ABC ,∠2= ∠ACB(角平分线的定义)
∴∠1+∠2= (∠ABC+∠ACB)= ×(180°-ɑ )=90°- ɑ
又∵∠BOC+∠1+∠2=180° (三角形的内角和定理)
A
B
C
E
F
O
1
2
例:如图,已知△ABC中,∠A=α ,∠ABC 和∠ACB的平分线BE、CF交于点O.求∠BOC
练习:如图,已知△ABC中,∠A=50°,∠ABC 和∠ACB的平分线BE、CF交于点O.求∠BOC
解:
∴ ∠ABC+∠ACB=180°-∠A(等式的性质)
又∵BE、CF分别平分∠ABC 和∠ACB(已知)
∴ ∠BOC=180°-(∠1+∠2)=180°-65°=115°(等式的性质)
∵∠A+∠ABC+∠ACB=180° (三角形的内角和定理)
∴ ∠ABC+∠ACB=180°-50°=130°(等量代换)
∴ ∠1= ∠ABC ∠2= ∠ACB(角平分线的定义)
∴∠1+∠2= (∠ABC+∠ACB)= ×130°=65°(等式的性质)
又∵∠BOC+∠1+∠2=180° (三角形的内角和定理)
A
B
C
E
F
O
1
2
课后作业
习题7.6 1,2.3,4
1.如图,已知∠B= 35° ,∠C=60°,
AD⊥BC,AE平分∠BAC,求∠EAD的度数.
解:在△ABC中,
∠BAC= 180°-B-∠C= 85°,
∵AD⊥ BC
∴∠ADE= 90°
∵AE平分∠BAC,
选做题:
2.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠DAC= 26° ,∠CBE=22°.求∠BAC的度数.
3.在△ABC中,∠B= 90°,AD平分∠CAE,CD平分∠ACF,AD、CD相交于点D.求∠D的度数 .
证明:在△ABC中,
∵∠B= 90°
∴∠BAC+∠BCA = 90°.
∵AD平分∠CAE,CD平分∠ACF.
∴∠DAC= ∠EAC
∠DCA= ∠FCA
= ( 180°-∠BAC)
= ( 180°-∠CBA)
∴∠DAC+∠DCA=
( 180°-∠BAC)+
( 180°-∠CBA)
=180°- (∠BAC+∠CBA)
=180°-45°=135°
∴∠D=
180°-135°=45°
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
