人教A版高中数学必修二第一章球的体积和表面积课件(共30张PPT)
文档属性
| 名称 | 人教A版高中数学必修二第一章球的体积和表面积课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-26 12:19:16 | ||
图片预览





文档简介
(共30张PPT)
1.3.2 球的体积和表面积
知识点 球的表面积和体积公式
1.球的表面积公式
(R为球的半径);
2.球的体积公式
S=4πR2
怎么得到的呢?
V=
πR3
怎样求球的表面积和体积?
提出问题
球既没有底面,也无法象柱、锥、台体一样展成平面图形,怎样求球的表面积和体积呢?
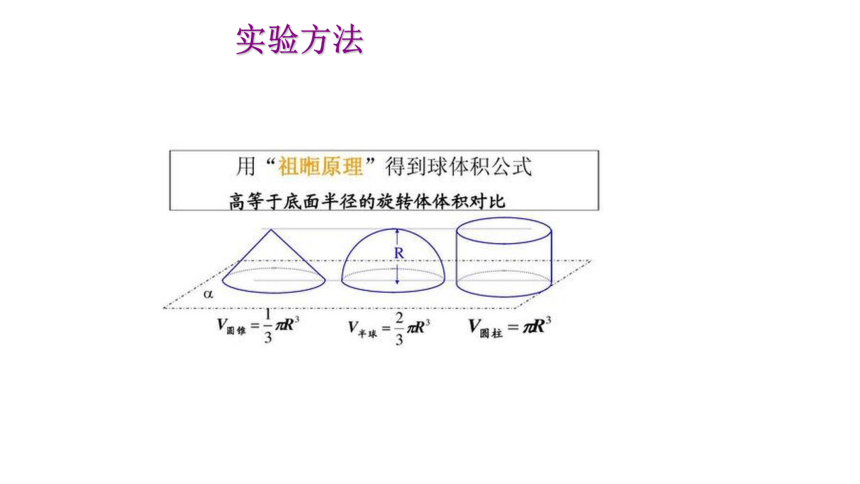
实验方法
h
实验:排液法测小球的体积
实验方法
小球的体积
等于
它排开液体的体积
曹冲称象
H
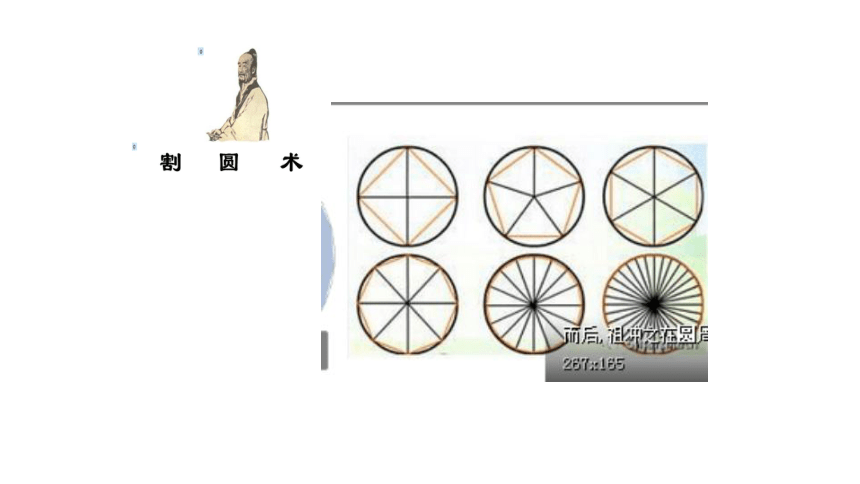
割
圆
术
早在公元三世纪,我国数学家刘徽为推导圆的面积公式而发明了“倍边法割圆术”.他用加倍的方式不断增加圆内接正多边形的边数,使其面积与圆的面积之差更小,即所谓“割之弥细,所失弥小”.这样重复下去,就达到了“割之又割,以至于不可再割,则与圆合体而无所失矣”.这是世界上最早的“极限”思想.
极限思想
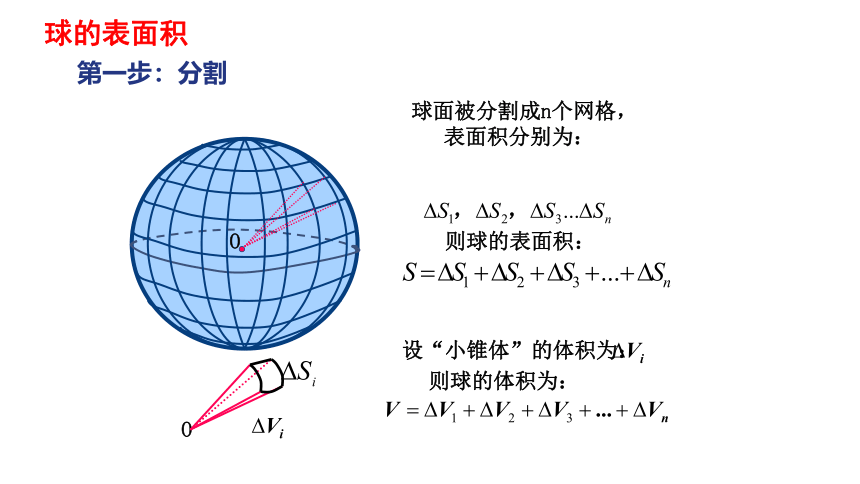
第一步:分割
O
球面被分割成n个网格,
表面积分别为:
则球的表面积:
则球的体积为:
设“小锥体”的体积为:
O
球的表面积
O
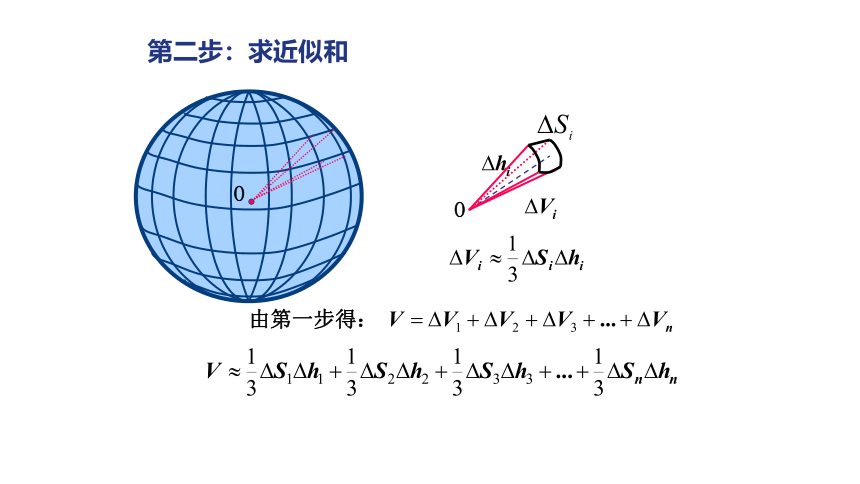
第二步:求近似和
O
由第一步得:
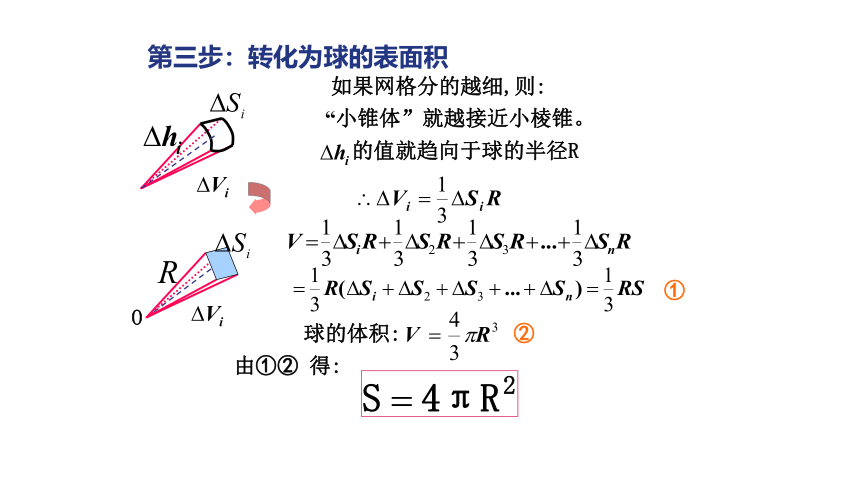
第三步:转化为球的表面积
如果网格分的越细,则:
①
由①②
得:
②
球的体积:
的值就趋向于球的半径R
O
“小锥体”就越接近小棱锥。
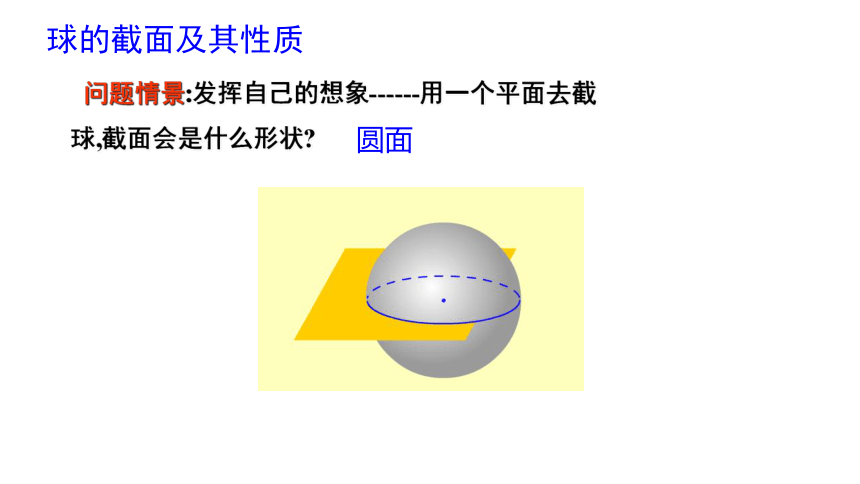
问题情景:发挥自己的想象------用一个平面去截球,截面会是什么形状?
球的截面及其性质
圆面
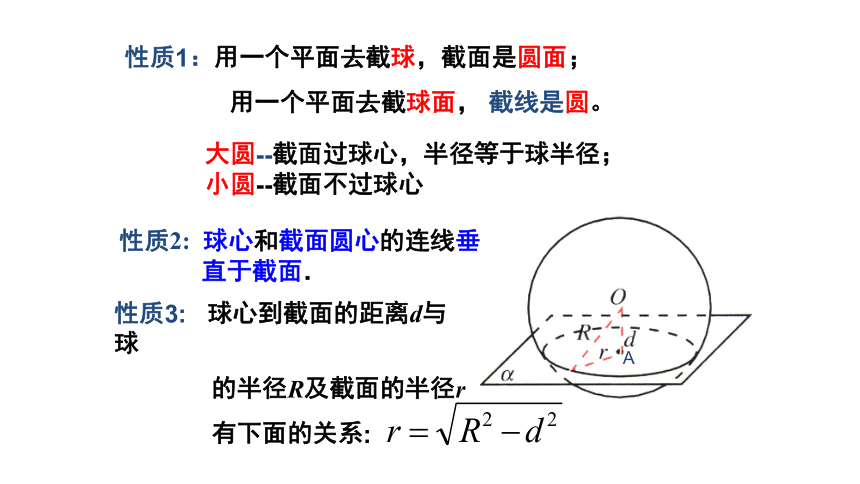
性质2:
球心和截面圆心的连线垂
直于截面.
性质1:用一个平面去截球,截面是圆面;
用一个平面去截球面,
截线是圆。
大圆--截面过球心,半径等于球半径;
小圆--截面不过球心
性质3:
球心到截面的距离d与球
的半径R及截面的半径r
有下面的关系:
A
例1 (1)已知球的表面积为64π,求它的体积;
类型一 球的体积和表面积
例2
两个球的体积之比为8∶27,那么这两个球的表面积之比为
例1 一个空间几何体的三视图如图所示,其中正视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的表面积为____.
类型二 与球有关的三视图问题
4π
例2(2016年辽宁卷)某个几何体的三视图如图所示,则这个几何体的表面积__________________
.
命题角度1 球的截面问题
类型三 球的截面及切接问题
例1 用一平面去截球所得截面的面积为2π,已知球心到该截面的距离为1,则该球的表面积为______.
例2
一个球内有相距9
cm的两个平行截面,它们的面积分别为49π
cm2和400π
cm2,
求球的表面积.
球与多面体的内切、外接
若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球
若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球
切点:各个面的中心。
球心:正方体的中心。
直径:相对两个面中心连线。
o
球的直径等于正方体棱长。
正方体的内切球(边长为a)
球心:正方体的中心。
直径:体对角线。
正方体的内切球,
外接球两心重合
正方体的外接球(边长为a)
长方体的外接球
球心:长方体的体对角线交点。
直径:体对角线。
没有
如果一个长方体有内切球,
那么它一定是
正方体
一般的长方体有内切球吗?
正四面体与球
1.求棱长为a的正四面体的外接球的半径R.
A
B
C
D
O
A
B
C
D
O
把正四面体补全为正方体,则正方体的边长为
故正四面体的外接球半径为
2.求棱长为a的正四面体的内切球的半径r.
正四面体的外接球和内切球的球心为什么重合?
所以
因为
所以
等体积法
A
B
C
M
O
R
R
边长为a正四面体的外接球,内切球还可利用直角三角形勾股定理来求
D
正四面体的外接球和内切球的球心重合,
是图中的O,则OS为外接球半径,
OM为内切球半径。
S
由于正四面体本身的对称性可知,内切球和外接球的两个球心是重合的,为正四面体高的四等分点,即内切球的半径为
(h
为正四面体的高),
且外接球的半径
,
(1)正多面体存在内切球且正多面体的中心为内切球的球心.
(2)求多面体内切球半径,往往可用“等体积法”.
(3)正四面体内切球半径是高的
,外接球半径是高的
.
(4)并非所有多面体都有内切球(或外接球).
命题角度2 与球有关的切、接问题
例3 (1)将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为
9π
解析 如图所示,将正四面体补形成一个正方体.
设正四面体的棱长为a.
又∵球的直径是正方体的体对角线,设球的半径是R,
规律与方法
3.常见的几何体与球的切、接问题的解决策略:
解决此类问题的实质就是根据几何体的相关数据求球的直径或半径,关键是根据“切点”和“接点”,作出轴截面图,把空间问题转化为平面问题来计算.
1.3.2 球的体积和表面积
知识点 球的表面积和体积公式
1.球的表面积公式
(R为球的半径);
2.球的体积公式
S=4πR2
怎么得到的呢?
V=
πR3
怎样求球的表面积和体积?
提出问题
球既没有底面,也无法象柱、锥、台体一样展成平面图形,怎样求球的表面积和体积呢?
实验方法
h
实验:排液法测小球的体积
实验方法
小球的体积
等于
它排开液体的体积
曹冲称象
H
割
圆
术
早在公元三世纪,我国数学家刘徽为推导圆的面积公式而发明了“倍边法割圆术”.他用加倍的方式不断增加圆内接正多边形的边数,使其面积与圆的面积之差更小,即所谓“割之弥细,所失弥小”.这样重复下去,就达到了“割之又割,以至于不可再割,则与圆合体而无所失矣”.这是世界上最早的“极限”思想.
极限思想
第一步:分割
O
球面被分割成n个网格,
表面积分别为:
则球的表面积:
则球的体积为:
设“小锥体”的体积为:
O
球的表面积
O
第二步:求近似和
O
由第一步得:
第三步:转化为球的表面积
如果网格分的越细,则:
①
由①②
得:
②
球的体积:
的值就趋向于球的半径R
O
“小锥体”就越接近小棱锥。
问题情景:发挥自己的想象------用一个平面去截球,截面会是什么形状?
球的截面及其性质
圆面
性质2:
球心和截面圆心的连线垂
直于截面.
性质1:用一个平面去截球,截面是圆面;
用一个平面去截球面,
截线是圆。
大圆--截面过球心,半径等于球半径;
小圆--截面不过球心
性质3:
球心到截面的距离d与球
的半径R及截面的半径r
有下面的关系:
A
例1 (1)已知球的表面积为64π,求它的体积;
类型一 球的体积和表面积
例2
两个球的体积之比为8∶27,那么这两个球的表面积之比为
例1 一个空间几何体的三视图如图所示,其中正视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的表面积为____.
类型二 与球有关的三视图问题
4π
例2(2016年辽宁卷)某个几何体的三视图如图所示,则这个几何体的表面积__________________
.
命题角度1 球的截面问题
类型三 球的截面及切接问题
例1 用一平面去截球所得截面的面积为2π,已知球心到该截面的距离为1,则该球的表面积为______.
例2
一个球内有相距9
cm的两个平行截面,它们的面积分别为49π
cm2和400π
cm2,
求球的表面积.
球与多面体的内切、外接
若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球
若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球
切点:各个面的中心。
球心:正方体的中心。
直径:相对两个面中心连线。
o
球的直径等于正方体棱长。
正方体的内切球(边长为a)
球心:正方体的中心。
直径:体对角线。
正方体的内切球,
外接球两心重合
正方体的外接球(边长为a)
长方体的外接球
球心:长方体的体对角线交点。
直径:体对角线。
没有
如果一个长方体有内切球,
那么它一定是
正方体
一般的长方体有内切球吗?
正四面体与球
1.求棱长为a的正四面体的外接球的半径R.
A
B
C
D
O
A
B
C
D
O
把正四面体补全为正方体,则正方体的边长为
故正四面体的外接球半径为
2.求棱长为a的正四面体的内切球的半径r.
正四面体的外接球和内切球的球心为什么重合?
所以
因为
所以
等体积法
A
B
C
M
O
R
R
边长为a正四面体的外接球,内切球还可利用直角三角形勾股定理来求
D
正四面体的外接球和内切球的球心重合,
是图中的O,则OS为外接球半径,
OM为内切球半径。
S
由于正四面体本身的对称性可知,内切球和外接球的两个球心是重合的,为正四面体高的四等分点,即内切球的半径为
(h
为正四面体的高),
且外接球的半径
,
(1)正多面体存在内切球且正多面体的中心为内切球的球心.
(2)求多面体内切球半径,往往可用“等体积法”.
(3)正四面体内切球半径是高的
,外接球半径是高的
.
(4)并非所有多面体都有内切球(或外接球).
命题角度2 与球有关的切、接问题
例3 (1)将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为
9π
解析 如图所示,将正四面体补形成一个正方体.
设正四面体的棱长为a.
又∵球的直径是正方体的体对角线,设球的半径是R,
规律与方法
3.常见的几何体与球的切、接问题的解决策略:
解决此类问题的实质就是根据几何体的相关数据求球的直径或半径,关键是根据“切点”和“接点”,作出轴截面图,把空间问题转化为平面问题来计算.
