六年级上册数学课件 第4单元《第3课时 比的应用》 人教版(共19张PPT)
文档属性
| 名称 | 六年级上册数学课件 第4单元《第3课时 比的应用》 人教版(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-26 00:00:00 | ||
图片预览






文档简介
第4单元 比
第3课时 比的应用
人教版数学六年级上册
1.理解按比例分配的意义。
2.理解按比例分配应用题的数量关系,并会解答此类应用题。
3.能运用所学知识来解决生活中的一些简单问题,体会数学与生活的密切联系。
学习目标
问题:
我班男女生人数各是多少?你能根据我班男女生人数用比的知识和分数的知识来说一句话吗?
学生汇报:
1.男生人数是女生人数的( ),男生人数和女生人数的比是( )
2.女生人数是男生人数的( ),女生人数和男生人数的比是( )
3.男生人数占全班人数的( ),男生人数和全班人数的比是( )
4.女生人数占全班人数的( ),女生人数和全班人数的比是( )
导入新知
口答:
1.把6个苹果平均分给两个小朋友,每人分几个?
2.六年级(1)班和二年级(1)班共同承担了面积为100平方米的卫生区保洁任务.六年级学生和二年级学生承担同样多的卫生区保洁任务,合理吗?这样分还是平均分吗?
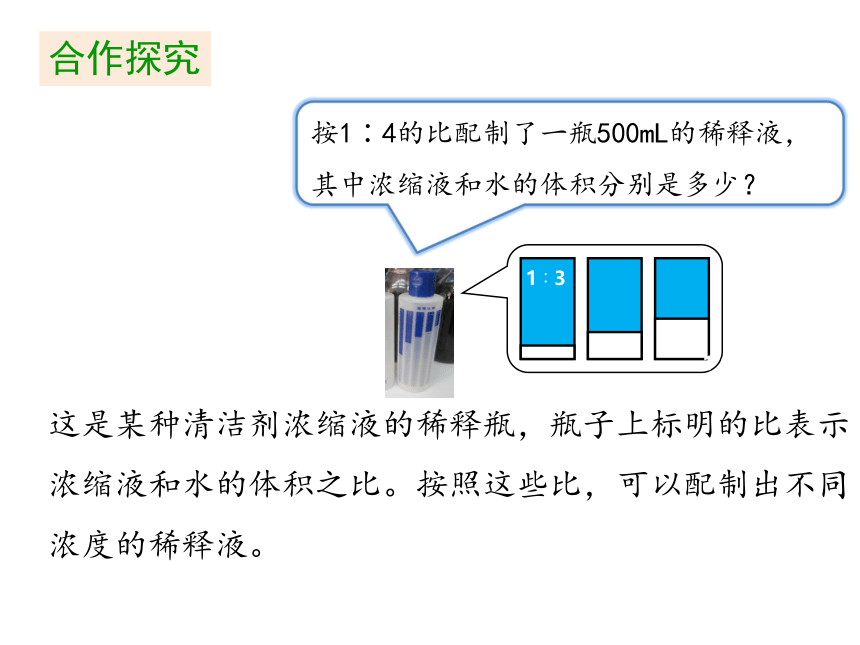
按1∶4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
1∶3
1∶4
1∶5
合作探究
1.在工农业生产和日常活动中,有时并不是把一个数量平均分配,而是需要把一个数量按照一定比来分配。
2.从某种意义上说,平均分是按一定的比分配的特例,按一定的比分配则是平均分配的发展。
3.例如:把一个数量平均分成2份,也就是说成把这个数量按1∶1进行分配。
明确意义
500mL是配好后的稀释液的体积,1∶4表示……
要求的是……
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知条件
按1∶4的比例配置了一瓶500mL的稀释液
所求问题
浓缩液和谁的体积分别是多少?
理解题意
按1∶4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
关键条件理解
500毫升稀释液
浓缩液
1份
水
4份
1∶4表示在500mL的稀释液中,浓缩液占1份,水占4份,一共是5份。
浓缩液占总体积的 。
1
1+4
每份是:
500÷5=100(mL)
浓缩液有:
100×1=100(mL)
水有:
100×4=400(mL)
1∶4
浓缩液有: 500× =100(mL)
水有:500× =( )(mL)
1
1+4
( )
( )
4
5
400
浓缩液
水
探究解题方法
把总体积平均分成5份……
500÷5=100(mL)
100×1=100(mL)
100×4=400(mL)
方法一:
方法二:
500× =100(mL)
1
1+4
500× =400(mL)
1
1+4
答:水的体积是400mL,浓缩液的体积是100mL。
探究解题方法
浓缩液体积∶水的体积
=( )∶( )
=( )∶( )
要看清楚1∶4到底是哪两个量之间的比。
100mL 400mL
1 4
答:浓缩液有 mL,水有 mL。
100 400
回顾与反思
1.爸爸用一根长108㎝的铁丝给亮亮做了一个长方体模型。这个模型长、宽、高的比是4:3:2,它的体积是多少立方厘米?
高 :108 × =24
9
2
答:它的体积是41472立方厘米。
宽 :108 × =36
9
3
108 × =48
9
4
长 :
体积: 48×36×24=41472(立方厘米)
课堂练习
方法二:
2. 某妇产科医院上月新生婴儿303名,男女婴儿人数之比是51︰50。上月新生男女婴儿各有多少人?
答:上月新生男婴儿有153人,女婴儿有150人。
51+50=101
303÷101=3(人)
3×51=153(人)
3×50=150(人)
101
50
303× =150(人)
101
51
303× =15(人)
51+50=101
方法一:
3. 学校把栽70棵树的任务,按照六年级三个班的人数分配给各班。一班46人,二班44人,三班50人。三个班各应栽树多少棵?
46︰44︰50= 23︰22︰25
23+22+25=70
70÷70=1(棵)
一班:1×23=23(棵)
二班:1×22=22(棵)
三班:1×25=25(棵)
方法一:
方法二:
46︰44︰50= 23︰22︰25
23+22+25
23
一班:70× =23(棵)
二班:70× =22(棵)
22
23+22+25
三班:70× =25(棵)
23+22+25
25
方法三:
46+44+50
46
一班:70× =23(棵)
46+44+50
44
二班:70× =22(棵)
三班:70× =25(棵)
46+44+50
25
46+44+50=140(人)
140÷70=2(人)
一班:46÷2=23(棵)
二班:44÷2=22(棵)
三班:50÷2=25(棵)
答:一班栽树23棵,二班栽树22棵,三班栽树25棵。
方法四:
1.可以先求出总份数,再求出一份是多少,然后求各部分的量。
2.还可以先求出各部分量占总量的百分之几,再求各部分的量。
如何解决按比分配问题?
归纳新知
再 见
第3课时 比的应用
人教版数学六年级上册
1.理解按比例分配的意义。
2.理解按比例分配应用题的数量关系,并会解答此类应用题。
3.能运用所学知识来解决生活中的一些简单问题,体会数学与生活的密切联系。
学习目标
问题:
我班男女生人数各是多少?你能根据我班男女生人数用比的知识和分数的知识来说一句话吗?
学生汇报:
1.男生人数是女生人数的( ),男生人数和女生人数的比是( )
2.女生人数是男生人数的( ),女生人数和男生人数的比是( )
3.男生人数占全班人数的( ),男生人数和全班人数的比是( )
4.女生人数占全班人数的( ),女生人数和全班人数的比是( )
导入新知
口答:
1.把6个苹果平均分给两个小朋友,每人分几个?
2.六年级(1)班和二年级(1)班共同承担了面积为100平方米的卫生区保洁任务.六年级学生和二年级学生承担同样多的卫生区保洁任务,合理吗?这样分还是平均分吗?
按1∶4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
1∶3
1∶4
1∶5
合作探究
1.在工农业生产和日常活动中,有时并不是把一个数量平均分配,而是需要把一个数量按照一定比来分配。
2.从某种意义上说,平均分是按一定的比分配的特例,按一定的比分配则是平均分配的发展。
3.例如:把一个数量平均分成2份,也就是说成把这个数量按1∶1进行分配。
明确意义
500mL是配好后的稀释液的体积,1∶4表示……
要求的是……
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知条件
按1∶4的比例配置了一瓶500mL的稀释液
所求问题
浓缩液和谁的体积分别是多少?
理解题意
按1∶4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
关键条件理解
500毫升稀释液
浓缩液
1份
水
4份
1∶4表示在500mL的稀释液中,浓缩液占1份,水占4份,一共是5份。
浓缩液占总体积的 。
1
1+4
每份是:
500÷5=100(mL)
浓缩液有:
100×1=100(mL)
水有:
100×4=400(mL)
1∶4
浓缩液有: 500× =100(mL)
水有:500× =( )(mL)
1
1+4
( )
( )
4
5
400
浓缩液
水
探究解题方法
把总体积平均分成5份……
500÷5=100(mL)
100×1=100(mL)
100×4=400(mL)
方法一:
方法二:
500× =100(mL)
1
1+4
500× =400(mL)
1
1+4
答:水的体积是400mL,浓缩液的体积是100mL。
探究解题方法
浓缩液体积∶水的体积
=( )∶( )
=( )∶( )
要看清楚1∶4到底是哪两个量之间的比。
100mL 400mL
1 4
答:浓缩液有 mL,水有 mL。
100 400
回顾与反思
1.爸爸用一根长108㎝的铁丝给亮亮做了一个长方体模型。这个模型长、宽、高的比是4:3:2,它的体积是多少立方厘米?
高 :108 × =24
9
2
答:它的体积是41472立方厘米。
宽 :108 × =36
9
3
108 × =48
9
4
长 :
体积: 48×36×24=41472(立方厘米)
课堂练习
方法二:
2. 某妇产科医院上月新生婴儿303名,男女婴儿人数之比是51︰50。上月新生男女婴儿各有多少人?
答:上月新生男婴儿有153人,女婴儿有150人。
51+50=101
303÷101=3(人)
3×51=153(人)
3×50=150(人)
101
50
303× =150(人)
101
51
303× =15(人)
51+50=101
方法一:
3. 学校把栽70棵树的任务,按照六年级三个班的人数分配给各班。一班46人,二班44人,三班50人。三个班各应栽树多少棵?
46︰44︰50= 23︰22︰25
23+22+25=70
70÷70=1(棵)
一班:1×23=23(棵)
二班:1×22=22(棵)
三班:1×25=25(棵)
方法一:
方法二:
46︰44︰50= 23︰22︰25
23+22+25
23
一班:70× =23(棵)
二班:70× =22(棵)
22
23+22+25
三班:70× =25(棵)
23+22+25
25
方法三:
46+44+50
46
一班:70× =23(棵)
46+44+50
44
二班:70× =22(棵)
三班:70× =25(棵)
46+44+50
25
46+44+50=140(人)
140÷70=2(人)
一班:46÷2=23(棵)
二班:44÷2=22(棵)
三班:50÷2=25(棵)
答:一班栽树23棵,二班栽树22棵,三班栽树25棵。
方法四:
1.可以先求出总份数,再求出一份是多少,然后求各部分的量。
2.还可以先求出各部分量占总量的百分之几,再求各部分的量。
如何解决按比分配问题?
归纳新知
再 见
