北师大版八年级数学上册 3.2 平面直角坐标系(第一课时 29张)
文档属性
| 名称 | 北师大版八年级数学上册 3.2 平面直角坐标系(第一课时 29张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-26 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
北师大版八年级上册
第三章
位置与坐标
3.2 平面直角坐标系(1)
学习目标
1. 理解平面直角坐标系以及横轴、纵轴、坐标轴、原点、象限、坐标等概念;(重点)
2. 能在给定的直角坐标系中,会根据坐标描出点的位置、由点的位置写出它的坐标.(难点)
1. 确定位置一般需要几个数据?
2. 什么是数轴?它的三个基本要素有哪些?
3. 数轴上的点与实数的关系?
复习回顾
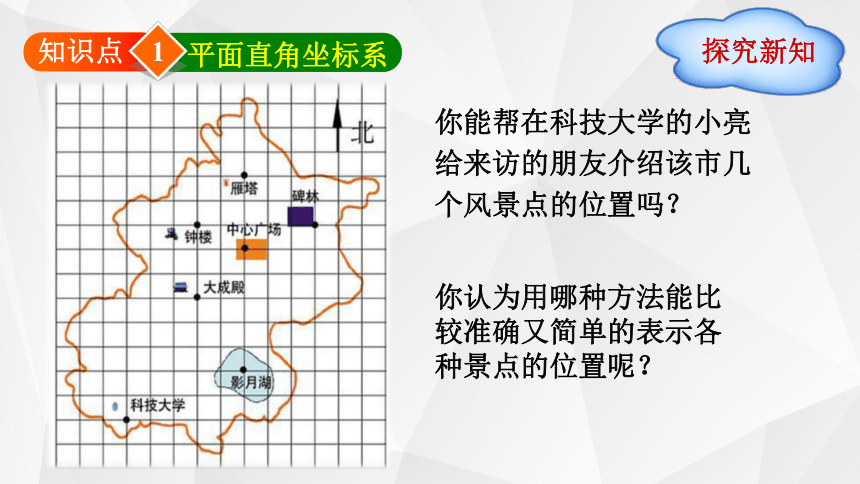
你能帮在科技大学的小亮给来访的朋友介绍该市几个风景点的位置吗?
你认为用哪种方法能比较准确又简单的表示各种景点的位置呢?
探究新知
1
知识点
平面直角坐标系
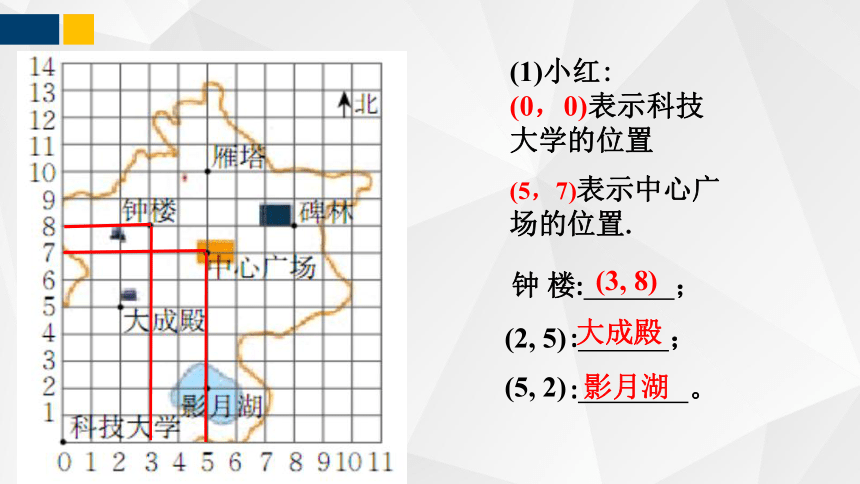
(1)小红:
(0,0)表示科技大学的位置
钟 楼: ;
: ;
: 。
(2, 5)
(5, 2)
(3, 8)
影月湖
大成殿
(5,7)表示中心广
场的位置.
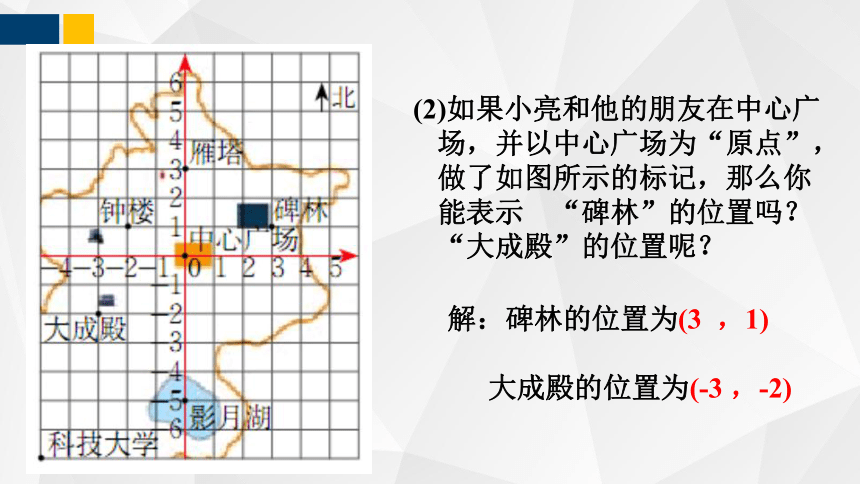
(2)如果小亮和他的朋友在中心广场,并以中心广场为“原点”,做了如图所示的标记,那么你能表示 “碑林”的位置吗?“大成殿”的位置呢?
解:碑林的位置为(3 ,1)
大成殿的位置为(-3 ,-2)
x轴
平面直角坐标系(如图)
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系(简称直角坐标系).
水平的叫x轴或横轴
竖直的叫y轴或纵轴
x轴取向右为正方向
y轴取向上为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
原点
y轴
三要素:(1)两条数轴;(2)互相垂直;(3)公共原点.
x
y
4
3
2
1
1 2 3 4
-1
-2
-3
-4
o
-3 -2 -1
x轴和y轴统称为坐标轴
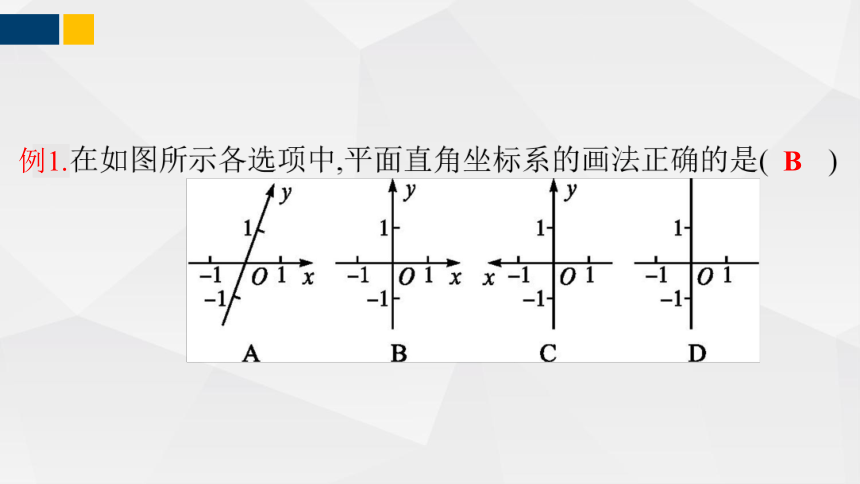
例1.
B
2
知识点
平面直角坐标系内点的坐标
对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标。
a
b
(a,b)
P
x
y
1
1
o
有序数对(a,b)是指:横坐标a写在前,纵坐标b写在后,中间用逗号隔开!
O
1
1
y
x
F
A
B
E
D
C
例2. 写出多边形ABCDEF各个顶点的坐标.
解:如图所示,各个顶点的
坐标分别为:
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
典例讲解
练习.如图,点A的坐标是 ,横坐标和纵坐标都是负数的点是 ,坐标是(2,-1)的点是 .
(3,3)
C
B
变式.如图为A,B,C三点在坐标平面上的位置图.若A,B,C的横坐标的数字总和为a,纵坐标的数字总和为b,则a-b的值是( )
A.5 B.3
C.-3 D.-5
A
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中找A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
做一做
做一做
x
y
(1)在平面直角坐标系中,描出下列各点:A(-5,0),B(1,4),C(3,3),D(1,0),E(3,-3),F(1,-4).
A
B
C
D
E
F
o
3
1
5
4
2
-2
-1
-3
1
2
3
4
5
-4
-3
-2
-1
-5
-4
x
y
(2)依次连接A,B,C,D,E,F,A,你得到什么图形?
A
B
C
D
E
F
(3)在平面直角坐标系中,点与实数对之间有何关系?
3
1
5
4
2
-2
-1
-3
1
2
3
4
5
-4
-3
-2
-1
-5
-4
0
结论:平面上的点与有序实数对是一一对应的
对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与它对应;
对于任意一对有序实数对,平面上都有唯一的一点与它对应.
注意:点(a,b)(a≠b)与点(b,a)是不同的两个点
例3:在平面直角坐标系中,和有序实数对一一对应的是( )
A.x轴上的所有点
B.y轴上的所有点
C.平面直角坐标内的所有点
D.x轴和y轴上的所有点
C
第一象限
第二象限
第三象限
第四象限
在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分.
x
y
4
3
2
1
1 2 3 4
-1
-2
-3
-4
o
-3 -2 -1
3
知识点
点的位置与点的坐标的关系
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
D
·
C
在直角坐标系中描出下列各点:
A(4,3) B(-2,3)
C(-4,-1) D(2,-2)
·
A
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,-1),
D(2.5,-2), E(0,-4)所在的象限吗?
观察:各象限点坐标符号特点.
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
结论:x轴上的点的纵坐标为0,y轴上的点的横坐标为0.
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
观察:坐标轴上点的坐标符号特点.
注意:坐标轴上的点不属于任何象限
例4. A,B,C,D四点在平直角坐标系中的位置如图所示,
则位于第二象限的点是( )
C
典例讲解
练习. 在平面直角坐标系中,点P(-2,-3)所在的象
限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
典例讲解
例5. 在平面直角坐标系中,点P(a+1, )所在的
象限是( )
A.x轴上 B.第二象限
C.y轴上 D.第四象限
D
典例讲解
例6.下列说法正确的是( )
A.若点P是直角坐标系中x轴上一点,且坐标为(a,b),
那么a=0.
B.若点P是直角坐标系中y轴上一点,且坐标为(a,b),
那么a=0.
C.若点P的横坐标为0,那么点P一定在x轴上.
D.若点P的坐标为(a,b),只要a,b中有一个为0,
点P就一定在y轴上.
B
2、如果点M(a+b,ab)在第二象限,那么点N(a,b)在第
象限。
练习.1、如果点A(a,b)在第四象限,那么点B(a,-b)在第
象限。
3、如果点P(m+3,m+1)在x轴上,则m的值是
4、已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
例7.已知点P的坐标为(2,-3),则它到x轴的距离为 ,
到y轴的距离为 .
变式. 若点P是第二象限的点,且点P到x轴的距离是4,到y轴
的距离是3,则点P的坐标是( )
A.(-4,3) B.(4,-3) C.(-3,4) D.(3,-4)
3
2
C
平面直角坐标系及点的坐标
平面直角坐标系:(1)两条数轴;(2)互相垂直;
(3)公共原点
四个象限
点的坐标
点的坐标的确定
描点
北师大版八年级上册
第三章
位置与坐标
3.2 平面直角坐标系(1)
学习目标
1. 理解平面直角坐标系以及横轴、纵轴、坐标轴、原点、象限、坐标等概念;(重点)
2. 能在给定的直角坐标系中,会根据坐标描出点的位置、由点的位置写出它的坐标.(难点)
1. 确定位置一般需要几个数据?
2. 什么是数轴?它的三个基本要素有哪些?
3. 数轴上的点与实数的关系?
复习回顾
你能帮在科技大学的小亮给来访的朋友介绍该市几个风景点的位置吗?
你认为用哪种方法能比较准确又简单的表示各种景点的位置呢?
探究新知
1
知识点
平面直角坐标系
(1)小红:
(0,0)表示科技大学的位置
钟 楼: ;
: ;
: 。
(2, 5)
(5, 2)
(3, 8)
影月湖
大成殿
(5,7)表示中心广
场的位置.
(2)如果小亮和他的朋友在中心广场,并以中心广场为“原点”,做了如图所示的标记,那么你能表示 “碑林”的位置吗?“大成殿”的位置呢?
解:碑林的位置为(3 ,1)
大成殿的位置为(-3 ,-2)
x轴
平面直角坐标系(如图)
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系(简称直角坐标系).
水平的叫x轴或横轴
竖直的叫y轴或纵轴
x轴取向右为正方向
y轴取向上为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
原点
y轴
三要素:(1)两条数轴;(2)互相垂直;(3)公共原点.
x
y
4
3
2
1
1 2 3 4
-1
-2
-3
-4
o
-3 -2 -1
x轴和y轴统称为坐标轴
例1.
B
2
知识点
平面直角坐标系内点的坐标
对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标。
a
b
(a,b)
P
x
y
1
1
o
有序数对(a,b)是指:横坐标a写在前,纵坐标b写在后,中间用逗号隔开!
O
1
1
y
x
F
A
B
E
D
C
例2. 写出多边形ABCDEF各个顶点的坐标.
解:如图所示,各个顶点的
坐标分别为:
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
典例讲解
练习.如图,点A的坐标是 ,横坐标和纵坐标都是负数的点是 ,坐标是(2,-1)的点是 .
(3,3)
C
B
变式.如图为A,B,C三点在坐标平面上的位置图.若A,B,C的横坐标的数字总和为a,纵坐标的数字总和为b,则a-b的值是( )
A.5 B.3
C.-3 D.-5
A
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中找A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
做一做
做一做
x
y
(1)在平面直角坐标系中,描出下列各点:A(-5,0),B(1,4),C(3,3),D(1,0),E(3,-3),F(1,-4).
A
B
C
D
E
F
o
3
1
5
4
2
-2
-1
-3
1
2
3
4
5
-4
-3
-2
-1
-5
-4
x
y
(2)依次连接A,B,C,D,E,F,A,你得到什么图形?
A
B
C
D
E
F
(3)在平面直角坐标系中,点与实数对之间有何关系?
3
1
5
4
2
-2
-1
-3
1
2
3
4
5
-4
-3
-2
-1
-5
-4
0
结论:平面上的点与有序实数对是一一对应的
对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与它对应;
对于任意一对有序实数对,平面上都有唯一的一点与它对应.
注意:点(a,b)(a≠b)与点(b,a)是不同的两个点
例3:在平面直角坐标系中,和有序实数对一一对应的是( )
A.x轴上的所有点
B.y轴上的所有点
C.平面直角坐标内的所有点
D.x轴和y轴上的所有点
C
第一象限
第二象限
第三象限
第四象限
在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分.
x
y
4
3
2
1
1 2 3 4
-1
-2
-3
-4
o
-3 -2 -1
3
知识点
点的位置与点的坐标的关系
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
D
·
C
在直角坐标系中描出下列各点:
A(4,3) B(-2,3)
C(-4,-1) D(2,-2)
·
A
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,-1),
D(2.5,-2), E(0,-4)所在的象限吗?
观察:各象限点坐标符号特点.
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
结论:x轴上的点的纵坐标为0,y轴上的点的横坐标为0.
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
观察:坐标轴上点的坐标符号特点.
注意:坐标轴上的点不属于任何象限
例4. A,B,C,D四点在平直角坐标系中的位置如图所示,
则位于第二象限的点是( )
C
典例讲解
练习. 在平面直角坐标系中,点P(-2,-3)所在的象
限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
典例讲解
例5. 在平面直角坐标系中,点P(a+1, )所在的
象限是( )
A.x轴上 B.第二象限
C.y轴上 D.第四象限
D
典例讲解
例6.下列说法正确的是( )
A.若点P是直角坐标系中x轴上一点,且坐标为(a,b),
那么a=0.
B.若点P是直角坐标系中y轴上一点,且坐标为(a,b),
那么a=0.
C.若点P的横坐标为0,那么点P一定在x轴上.
D.若点P的坐标为(a,b),只要a,b中有一个为0,
点P就一定在y轴上.
B
2、如果点M(a+b,ab)在第二象限,那么点N(a,b)在第
象限。
练习.1、如果点A(a,b)在第四象限,那么点B(a,-b)在第
象限。
3、如果点P(m+3,m+1)在x轴上,则m的值是
4、已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
例7.已知点P的坐标为(2,-3),则它到x轴的距离为 ,
到y轴的距离为 .
变式. 若点P是第二象限的点,且点P到x轴的距离是4,到y轴
的距离是3,则点P的坐标是( )
A.(-4,3) B.(4,-3) C.(-3,4) D.(3,-4)
3
2
C
平面直角坐标系及点的坐标
平面直角坐标系:(1)两条数轴;(2)互相垂直;
(3)公共原点
四个象限
点的坐标
点的坐标的确定
描点
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
