人教版八年级数学上册13.1.2线段垂直平分线的性质课件(共24张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.1.2线段垂直平分线的性质课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 671.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 08:45:47 | ||
图片预览







文档简介
每课5分钟 宽容事例分享:
亚伯拉罕·林肯是美国第 16 任总统,领导了拯救联邦和结束奴隶制度的伟大斗争。尽管他仅在边疆受过一点儿初级教育,担任公职的经验也很少,然而,他那敏锐的洞察力和宽容深厚的人道主义意识,使他成了美国历史上最伟大的总统。
有人批评林肯总统对待政敌的态度:“你为什么试图让他们变成朋友呢?你应该想办法打击他们,消灭他们才对。” 林肯总统温和地说:“我们难道不是在消灭政敌吗?当我们成为朋友时,政敌就不存在了。”。这就是林肯总统消灭政敌的方法,将敌人变成朋友。他,两度被选为美国总统。
今天在以他名字命名的纪念馆的墙壁上刻著的是这样的一段话:“对任何人不怀恶意;对一切人宽大仁爱;坚持正义,因为上帝使我们懂得正义;让我们继续努力去完成我们正在从事的事业;包扎我们国家的伤口。”
宽容是做人的美德
应该宽容地对待不同意见
宽容是一种人生境界
宽容是社会文明的标志
家庭 学校 中也需要宽容
13.1.2 线段的垂直平分线(1)
性质与判定
3.会用尺规经过已知直线外一点作这条直线的垂线,了解作图的道理.
1. 理解线段垂直平分线的性质和判定.
2. 能运用线段垂直平分线的性质和判定解决实际问题.
素养目标
线段的垂直平分线
我们曾经利用折纸的方法得到:
线段垂直平分线上的点到这条线段两个端点距离相等.
你能证明这一结论吗?
回顾 思考
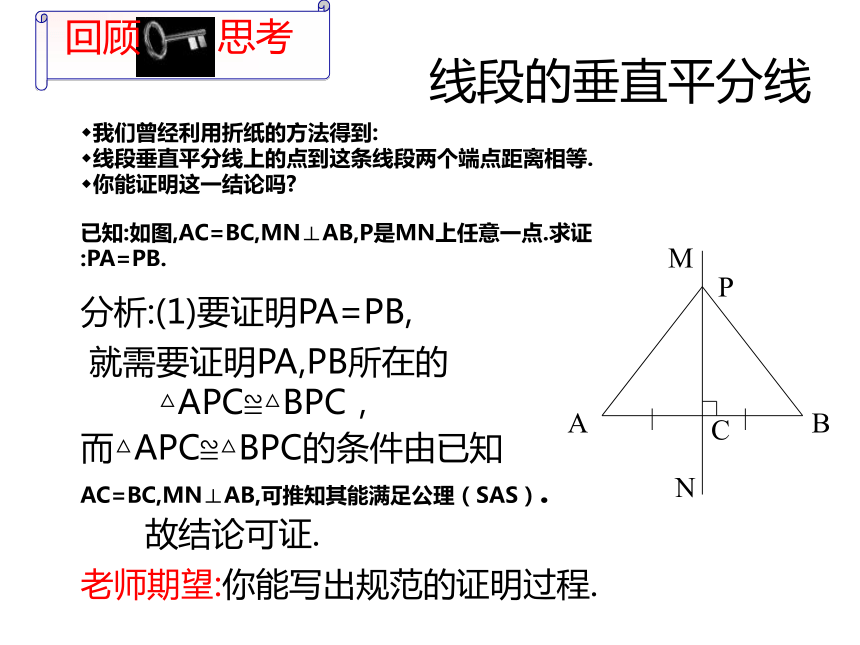
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.
A
C
B
P
M
N
分析:(1)要证明PA=PB,
而△APC≌△BPC的条件由已知
故结论可证.
老师期望:你能写出规范的证明过程.
AC=BC,MN⊥AB,可推知其能满足公理(SAS).
就需要证明PA,PB所在的△APC≌△BPC,
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
实际问题1
导入新知
你能用不同的方法验证这一结论吗?
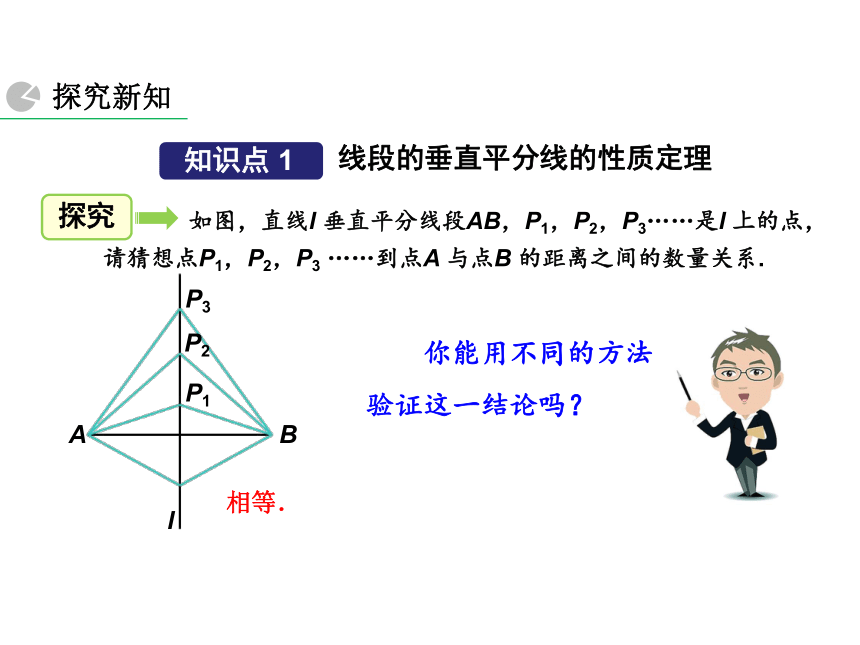
如图,直线l 垂直平分线段AB,P1,P2,P3……是l 上的点,请猜想点P1,P2,P3 ……到点A 与点B 的距离之间的数量关系.
相等.
A
B
l
P1
P2
P3
线段的垂直平分线的性质定理
探究新知
知识点 1
探究
用符号语言表示为:∵ CA =CB,l⊥AB,∴ PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
A
B
P
C
l
探究新知
猜想与证明
线段垂直平分线的性质:
线段垂直平分线上的点到这条线段两个端点的距离相等.
探究新知
归纳总结
几何的三种语言
定理 线段垂直平分线上的点到这条线段两个端点距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.
开启 智慧
A
C
B
P
M
N
如图,
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
1.如图,在△ABC 中,BC =8,AB 的垂直平分线交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等于___.
A
B
C
D
E
8
巩固练习
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.
2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
A
B
C
D
E
巩固练习
A
B
C
D
E
解: AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .
巩固练习
2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
进步的标志
′
驶向胜利的彼岸
思考分析
你能写出“定理 线段垂直平分线上的点到这条线段两个端点距离相等”的逆命题吗?
逆命题 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
它是真命题吗?
A
B
P
如果是.请你证明它.
已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.
分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或AB的中点,),然后证明另一个结论正确.
想一想:若作出∠P的角平分线,结论是否也可以得证?
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
P
A
B
C
线段的垂直平分线的判定定理
探究新知
知识点 2
探究
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
探究新知
驶向胜利的彼岸
逆定理
我能行
1
逆定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
C
B
P
M
N
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
从这个结果出发,你还能联想到什么?
驶向胜利的彼岸
尺规作图
做一做
1
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.
A
B
C
D
2. 作直线CD.
则直线CD就是线段AB的垂直平分线.
请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
老师提示:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.
挑战自我
随堂练习
1
驶向胜利的彼岸
如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.
老师期望:
你能说出填空结果的根据.
E
D
A
B
C
7
60
1.如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于点D,若△DBC的周长为35 cm,则BC的长为( )
A.5 cm B.10 cm
C.15 cm D.17.5 cm
基础巩固题
C
课堂检测
2.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
C
C
课堂检测
基础巩固题
3.如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长为 cm.
7.8
4. 如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段 __________ 的垂直平分线上.
AC
解析:∵BC=BD+AD,
又∵BC=BD+DC,
∴AD=DC.
∴点D在线段AC的垂直平分线上.
课堂检测
基础巩固题
回味无穷
定理
线段垂直平分线上的点到这条线段两个端点距离相等.
如图,
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
逆定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
小结 拓展
A
C
B
P
M
N
线段的垂直平分线
性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
集合
定义
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.
关系
PA=PB
点P在线段AB的垂直平分线上
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
课堂小结
亚伯拉罕·林肯是美国第 16 任总统,领导了拯救联邦和结束奴隶制度的伟大斗争。尽管他仅在边疆受过一点儿初级教育,担任公职的经验也很少,然而,他那敏锐的洞察力和宽容深厚的人道主义意识,使他成了美国历史上最伟大的总统。
有人批评林肯总统对待政敌的态度:“你为什么试图让他们变成朋友呢?你应该想办法打击他们,消灭他们才对。” 林肯总统温和地说:“我们难道不是在消灭政敌吗?当我们成为朋友时,政敌就不存在了。”。这就是林肯总统消灭政敌的方法,将敌人变成朋友。他,两度被选为美国总统。
今天在以他名字命名的纪念馆的墙壁上刻著的是这样的一段话:“对任何人不怀恶意;对一切人宽大仁爱;坚持正义,因为上帝使我们懂得正义;让我们继续努力去完成我们正在从事的事业;包扎我们国家的伤口。”
宽容是做人的美德
应该宽容地对待不同意见
宽容是一种人生境界
宽容是社会文明的标志
家庭 学校 中也需要宽容
13.1.2 线段的垂直平分线(1)
性质与判定
3.会用尺规经过已知直线外一点作这条直线的垂线,了解作图的道理.
1. 理解线段垂直平分线的性质和判定.
2. 能运用线段垂直平分线的性质和判定解决实际问题.
素养目标
线段的垂直平分线
我们曾经利用折纸的方法得到:
线段垂直平分线上的点到这条线段两个端点距离相等.
你能证明这一结论吗?
回顾 思考
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.
A
C
B
P
M
N
分析:(1)要证明PA=PB,
而△APC≌△BPC的条件由已知
故结论可证.
老师期望:你能写出规范的证明过程.
AC=BC,MN⊥AB,可推知其能满足公理(SAS).
就需要证明PA,PB所在的△APC≌△BPC,
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
实际问题1
导入新知
你能用不同的方法验证这一结论吗?
如图,直线l 垂直平分线段AB,P1,P2,P3……是l 上的点,请猜想点P1,P2,P3 ……到点A 与点B 的距离之间的数量关系.
相等.
A
B
l
P1
P2
P3
线段的垂直平分线的性质定理
探究新知
知识点 1
探究
用符号语言表示为:∵ CA =CB,l⊥AB,∴ PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
A
B
P
C
l
探究新知
猜想与证明
线段垂直平分线的性质:
线段垂直平分线上的点到这条线段两个端点的距离相等.
探究新知
归纳总结
几何的三种语言
定理 线段垂直平分线上的点到这条线段两个端点距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.
开启 智慧
A
C
B
P
M
N
如图,
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
1.如图,在△ABC 中,BC =8,AB 的垂直平分线交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等于___.
A
B
C
D
E
8
巩固练习
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.
2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
A
B
C
D
E
巩固练习
A
B
C
D
E
解: AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .
巩固练习
2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
进步的标志
′
驶向胜利的彼岸
思考分析
你能写出“定理 线段垂直平分线上的点到这条线段两个端点距离相等”的逆命题吗?
逆命题 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
它是真命题吗?
A
B
P
如果是.请你证明它.
已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.
分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或AB的中点,),然后证明另一个结论正确.
想一想:若作出∠P的角平分线,结论是否也可以得证?
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
P
A
B
C
线段的垂直平分线的判定定理
探究新知
知识点 2
探究
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
探究新知
驶向胜利的彼岸
逆定理
我能行
1
逆定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
C
B
P
M
N
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
从这个结果出发,你还能联想到什么?
驶向胜利的彼岸
尺规作图
做一做
1
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.
A
B
C
D
2. 作直线CD.
则直线CD就是线段AB的垂直平分线.
请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
老师提示:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.
挑战自我
随堂练习
1
驶向胜利的彼岸
如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.
老师期望:
你能说出填空结果的根据.
E
D
A
B
C
7
60
1.如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于点D,若△DBC的周长为35 cm,则BC的长为( )
A.5 cm B.10 cm
C.15 cm D.17.5 cm
基础巩固题
C
课堂检测
2.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
C
C
课堂检测
基础巩固题
3.如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长为 cm.
7.8
4. 如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段 __________ 的垂直平分线上.
AC
解析:∵BC=BD+AD,
又∵BC=BD+DC,
∴AD=DC.
∴点D在线段AC的垂直平分线上.
课堂检测
基础巩固题
回味无穷
定理
线段垂直平分线上的点到这条线段两个端点距离相等.
如图,
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
逆定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
小结 拓展
A
C
B
P
M
N
线段的垂直平分线
性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
集合
定义
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.
关系
PA=PB
点P在线段AB的垂直平分线上
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
课堂小结
