人教版九年级上册数学24.2.1点和圆的位置关系课件(共23张PPT)
文档属性
| 名称 | 人教版九年级上册数学24.2.1点和圆的位置关系课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 329.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 00:00:00 | ||
图片预览




文档简介
24.2.1点和圆的位置关系
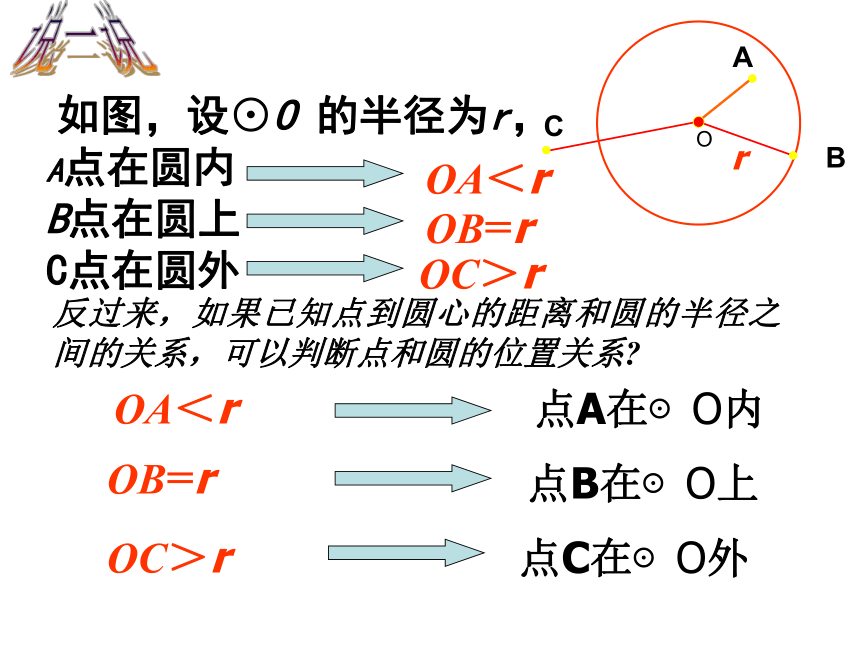
如图,设⊙O 的半径为r,
A点在圆内
B点在圆上
C点在圆外
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来,如果已知点到圆心的距离和圆的半径之间的关系,可以判断点和圆的位置关系?
OA<r
OB=r
OC>r
A
B
C
r
OA<r
OB=r
OC>r
说一说
O
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习:已知圆的半径等于5厘米,若点到圆心的距离是:
⑴8厘米 ⑵4厘米 ⑶5厘米。
请你分别说出点与圆的位置关系。
●
●
●
●
O
符号 读作“等价
于”,它表示从符号
的左端可以得到右端,从
右端也可以得到左端.
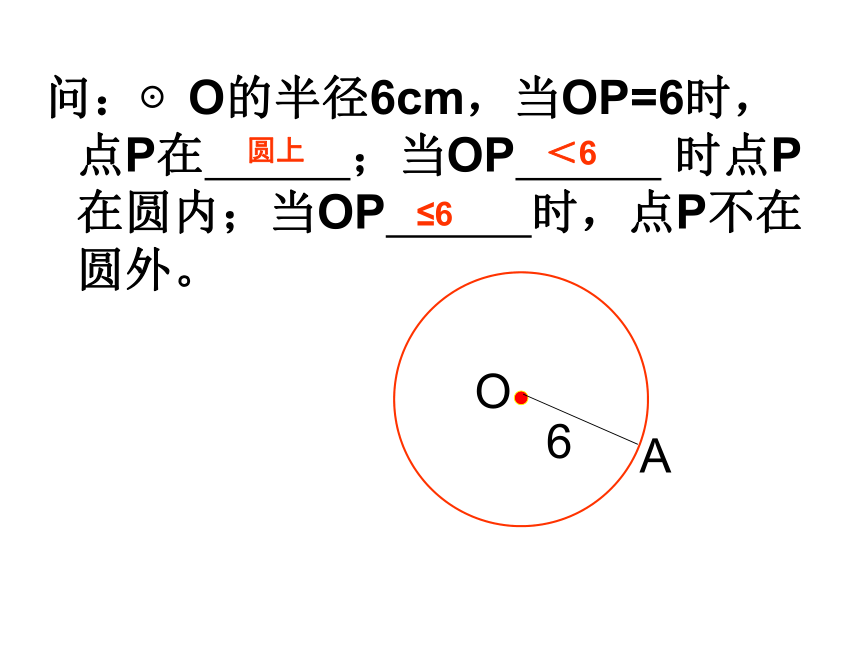
问:⊙O的半径6cm,当OP=6时,点P在 ;当OP 时点P在圆内;当OP 时,点P不在圆外。
圆上
<6
≤6
A
6
O
点A在
点B在
点C在
测一测
∵OA=8<10 ∴点A在圆内
∵OB=10=10 ∴点B在圆上
∵OC=12>10 ∴点C在圆外
圆内
圆上
圆外
1.⊙O的半径10cm,A、B、C三点到圆心
的距离分别为8cm、10cm、12cm,则
点A、B、C与⊙O的位置关系是:
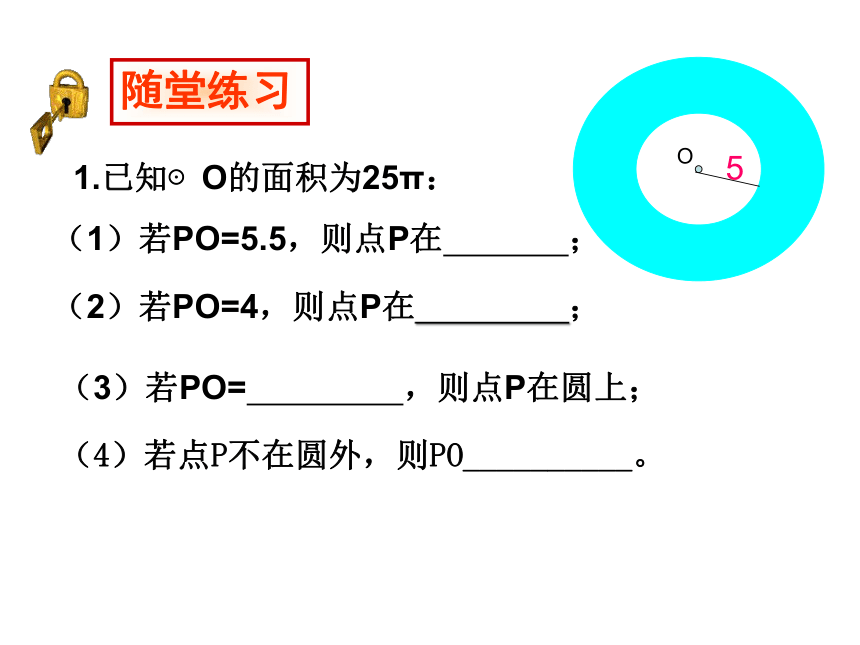
1.已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO__________。
随堂练习
O
O
5
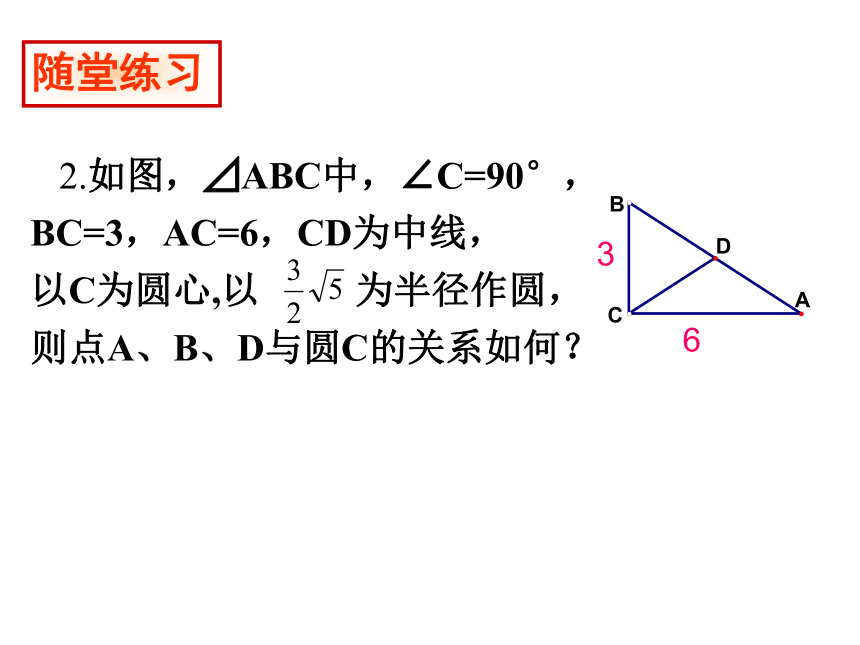
2.如图,⊿ABC中,∠C=90°,
BC=3,AC=6,CD为中线,
以C为圆心,以 为半径作圆,
则点A、B、D与圆C的关系如何?
随堂练习
6
3
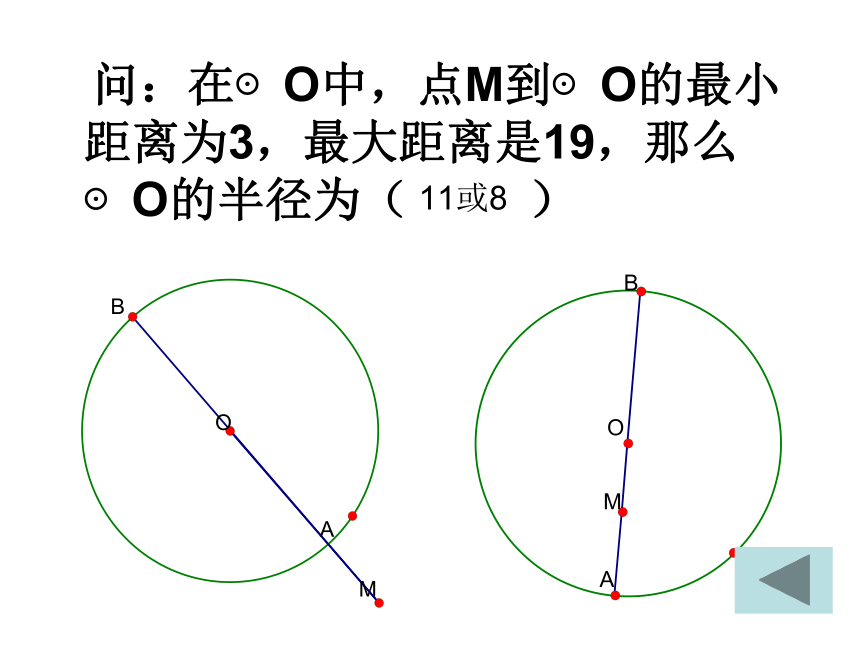
问:在⊙O中,点M到⊙O的最小距离为3,最大距离是19,那么⊙O的半径为( )
11或8
唐朝的铜镜是中国铜镜中的精品。江西省文物考古研究所日前从玉山县一座唐代墓葬中出土了半面铜镜,那么你有什么方法使得它能“破镜重圆”呢?
A
B
0
C
对于一个圆来说,过几个点能作一个圆,并且只能作一个圆?
类比探究:
过一点能作几个圆?
无数个
A
过A点的圆的圆心有何特点?
平面上除A点外的任意一点
探索一
经过一个已知点A能确定一个圆吗?
A
经过一个已知点能作无数个圆
过两点能作几个圆?
A
B
过A、B两点的圆的圆心有何特点?
经过两点A,B的圆的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
●O
●O
探索二
经过两个已知点A、B能确定一个圆吗?
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
它们的圆心都在线段AB的中垂线上。
A
B
C
为什么过同一直线上的三点不能作圆呢?
因为DE∥FG,所以没有交点,
即没有过这三点的圆心
D
F
E
G
1.当三点共线
(不能作圆)
参见课本P92反证法
探索三
经过三个已知点A,B,C能确定一个圆吗?
A
B
C
1、连结AB,作线段AB的垂直平分线DE,
O
D
E
G
F
2、连结BC,作线段BC的垂直平分线FG,交DE于点O ,
3、以O为圆心,OB为半径作圆,
作法:
⊙O就是所求作的圆
已知:不在同一直线上的三点 A、B、C
求作:⊙O,使它经过A、B、C
2、当三点不共线
定理:
不在同一直线上的三点确定一个圆.
O
A
B
C
我们的收获
O
1.由定理可知:经过三角形三个顶点可以作一个圆.并且只能作一个圆.
2.经过三角形各顶点的圆叫做三角形的外接圆。
3.三角形外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形。
A
B
C
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
外心
1.三边垂直平分线的交点
2.到三个顶点距离相等
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
想一想
O
A
B
C
A
B
C
O
直角三角形外心是斜边AB的中点
钝角三角形外心在△ABC的外面
三角形的外心是否一定在三角形的内部?
试一试
画出以下三角形的外接圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
思 考
1、比较这三个三角形外心的位置,你有何发现?
(图1)
(图2)
(图3)
2、图2中,若AB=3,BC=4,则它的外接圆半径是多少?
锐角三角形的外心位于三角形内部,直角三角形的外心位于斜边的中点,钝角三角形的外心位于三角形外部.
课堂练习
判断题:
1、过三点一定可以作圆 ( )
5、三角形的外心到三边的距离相等 ( )
2、三角形有且只有一个外接圆 ( )
3、任意一个圆有一个内接三角形,
并且只有一个内接三角形 ( )
4、三角形的外心就是这个三角形任意两边
垂直平分线的交点 ( )
思考:过任意四个点是不是一定可以作一个圆?请举例说明.
不一定
1.四点在一条直线上不能作圆;
3.四点中任意三点不在一条直线可能作圆也可能作不出一个圆.
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
2.三点在同一直线上,另一点不在这条直线上不能作圆;
如图,设⊙O 的半径为r,
A点在圆内
B点在圆上
C点在圆外
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来,如果已知点到圆心的距离和圆的半径之间的关系,可以判断点和圆的位置关系?
OA<r
OB=r
OC>r
A
B
C
r
OA<r
OB=r
OC>r
说一说
O
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习:已知圆的半径等于5厘米,若点到圆心的距离是:
⑴8厘米 ⑵4厘米 ⑶5厘米。
请你分别说出点与圆的位置关系。
●
●
●
●
O
符号 读作“等价
于”,它表示从符号
的左端可以得到右端,从
右端也可以得到左端.
问:⊙O的半径6cm,当OP=6时,点P在 ;当OP 时点P在圆内;当OP 时,点P不在圆外。
圆上
<6
≤6
A
6
O
点A在
点B在
点C在
测一测
∵OA=8<10 ∴点A在圆内
∵OB=10=10 ∴点B在圆上
∵OC=12>10 ∴点C在圆外
圆内
圆上
圆外
1.⊙O的半径10cm,A、B、C三点到圆心
的距离分别为8cm、10cm、12cm,则
点A、B、C与⊙O的位置关系是:
1.已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO__________。
随堂练习
O
O
5
2.如图,⊿ABC中,∠C=90°,
BC=3,AC=6,CD为中线,
以C为圆心,以 为半径作圆,
则点A、B、D与圆C的关系如何?
随堂练习
6
3
问:在⊙O中,点M到⊙O的最小距离为3,最大距离是19,那么⊙O的半径为( )
11或8
唐朝的铜镜是中国铜镜中的精品。江西省文物考古研究所日前从玉山县一座唐代墓葬中出土了半面铜镜,那么你有什么方法使得它能“破镜重圆”呢?
A
B
0
C
对于一个圆来说,过几个点能作一个圆,并且只能作一个圆?
类比探究:
过一点能作几个圆?
无数个
A
过A点的圆的圆心有何特点?
平面上除A点外的任意一点
探索一
经过一个已知点A能确定一个圆吗?
A
经过一个已知点能作无数个圆
过两点能作几个圆?
A
B
过A、B两点的圆的圆心有何特点?
经过两点A,B的圆的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
●O
●O
探索二
经过两个已知点A、B能确定一个圆吗?
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
它们的圆心都在线段AB的中垂线上。
A
B
C
为什么过同一直线上的三点不能作圆呢?
因为DE∥FG,所以没有交点,
即没有过这三点的圆心
D
F
E
G
1.当三点共线
(不能作圆)
参见课本P92反证法
探索三
经过三个已知点A,B,C能确定一个圆吗?
A
B
C
1、连结AB,作线段AB的垂直平分线DE,
O
D
E
G
F
2、连结BC,作线段BC的垂直平分线FG,交DE于点O ,
3、以O为圆心,OB为半径作圆,
作法:
⊙O就是所求作的圆
已知:不在同一直线上的三点 A、B、C
求作:⊙O,使它经过A、B、C
2、当三点不共线
定理:
不在同一直线上的三点确定一个圆.
O
A
B
C
我们的收获
O
1.由定理可知:经过三角形三个顶点可以作一个圆.并且只能作一个圆.
2.经过三角形各顶点的圆叫做三角形的外接圆。
3.三角形外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形。
A
B
C
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
外心
1.三边垂直平分线的交点
2.到三个顶点距离相等
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
想一想
O
A
B
C
A
B
C
O
直角三角形外心是斜边AB的中点
钝角三角形外心在△ABC的外面
三角形的外心是否一定在三角形的内部?
试一试
画出以下三角形的外接圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
思 考
1、比较这三个三角形外心的位置,你有何发现?
(图1)
(图2)
(图3)
2、图2中,若AB=3,BC=4,则它的外接圆半径是多少?
锐角三角形的外心位于三角形内部,直角三角形的外心位于斜边的中点,钝角三角形的外心位于三角形外部.
课堂练习
判断题:
1、过三点一定可以作圆 ( )
5、三角形的外心到三边的距离相等 ( )
2、三角形有且只有一个外接圆 ( )
3、任意一个圆有一个内接三角形,
并且只有一个内接三角形 ( )
4、三角形的外心就是这个三角形任意两边
垂直平分线的交点 ( )
思考:过任意四个点是不是一定可以作一个圆?请举例说明.
不一定
1.四点在一条直线上不能作圆;
3.四点中任意三点不在一条直线可能作圆也可能作不出一个圆.
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
2.三点在同一直线上,另一点不在这条直线上不能作圆;
同课章节目录
