人教版八年级数学上册15.3分式方程——巧解分式方程课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册15.3分式方程——巧解分式方程课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 913.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 23:49:06 | ||
图片预览








文档简介
15.3 巧解分式方程
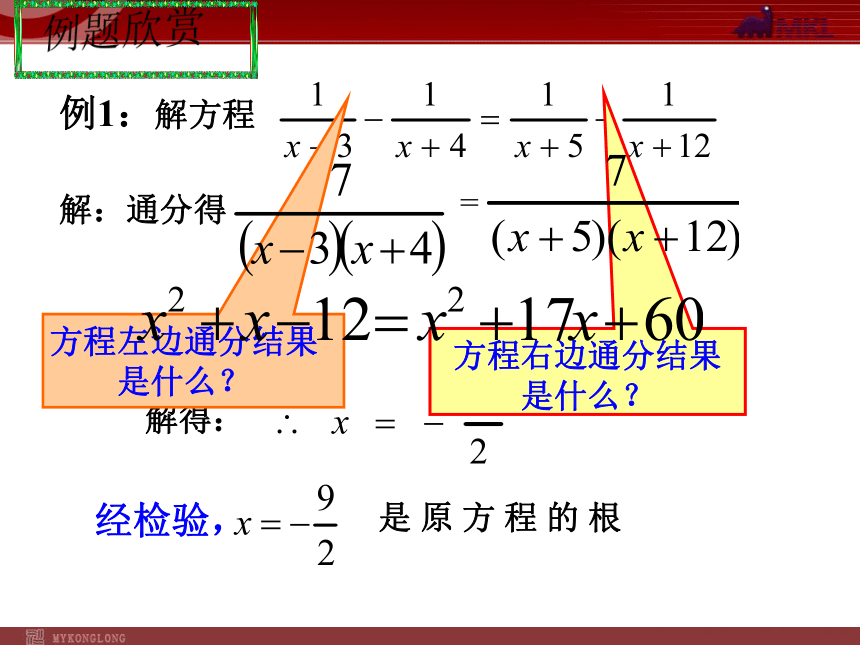
解得:
例1:解方程
方程左边通分结果是什么?
方程右边通分结果是什么?
经检验,
是 原 方 程 的 根
解:通分得
=
例题欣赏
像例1 这样的方程用常规解法往往复杂,采取局部通分法,会使解法很简单.这种解法称为 ——通 分 法
特别提醒
知道了吗?
会用了吗?
掌握了吗?
解方程
动动脑
还
有
其
它
解
法
吗
解
例3 :解方程
点拨: 此方程的特点是:各分式的分子与分母的次数相同, 这样一般可将各分式拆成: 整式+分式 的形式。
例题欣赏
特别提醒
知道了吗?
会用了吗?
掌握了吗?
像例3 各分式的分子、分母的次数相同,且相差一定的数,可将各分式拆成几项的和。这种解法称为 —— 拆 项 法
解:原方程可化为
解方程:
解:原方程可化为
两边都乘以
,并整理得;
解得
检验:x=1是原方程的根,x=2是增根
∴原方程的根是x=1
例题欣赏
∴x= 是增根,舍去.
解方程:
x(x-2)
解:方程两边同乘以最简公分母 ,
x 2+ x -6=0
化简,得
解得 x1= x2=
检验:把x1= 代入最简公分母, x(x-2)≠0;
把x2= 代入最简公分母, x(x-2)=0
∴原方程的根是x=
2
-3
-3
2
2
-3
解方程
解:原方程可化为
两边都乘以
得
化简整理得
解得
∴经检验:
是原方程的解
还有其它方法吗?
例题欣赏
解:原方程可化为
,方程化为
解得
可设
当
即
解得:
当
即
此方程无解
∴经检验:
是原方程的解
例题欣赏
特别提醒
知道了吗?
会用了吗?
掌握了吗?
象以上这种用一个字母(y) 来代替原方程中的一个较复杂的代数式 从而使原
方程简化,易于求解的方法,叫换元法
y
设 x2 + x =
y
y
下面的过程请同学们自己完成
相信你们能行
以下各方程能利用换元法进行换元吗?
能
不能
能
小结
有些分式方程用常规方法-----------去分母,是很复杂 ,甚至无法求解,有时要采取其他的方法
②各分式的分子、分母的次数相同,且相差一定的数,可将各分式拆成几项的和。这种解法称为 —— 拆 项 法
①采取局部通分法,会使解法很简单.这种解法称为 ——通 分 法
⑶用一个字母来代替原方程中的一个较复杂的代数式 ,从而使原方程简化,易于求解的方法,叫换元法
教师寄语
解分式方程的方法还很多,我们只讲了有限的一点,希望同学们课后自己去发现,相信同学们有更大的收获。
解得:
例1:解方程
方程左边通分结果是什么?
方程右边通分结果是什么?
经检验,
是 原 方 程 的 根
解:通分得
=
例题欣赏
像例1 这样的方程用常规解法往往复杂,采取局部通分法,会使解法很简单.这种解法称为 ——通 分 法
特别提醒
知道了吗?
会用了吗?
掌握了吗?
解方程
动动脑
还
有
其
它
解
法
吗
解
例3 :解方程
点拨: 此方程的特点是:各分式的分子与分母的次数相同, 这样一般可将各分式拆成: 整式+分式 的形式。
例题欣赏
特别提醒
知道了吗?
会用了吗?
掌握了吗?
像例3 各分式的分子、分母的次数相同,且相差一定的数,可将各分式拆成几项的和。这种解法称为 —— 拆 项 法
解:原方程可化为
解方程:
解:原方程可化为
两边都乘以
,并整理得;
解得
检验:x=1是原方程的根,x=2是增根
∴原方程的根是x=1
例题欣赏
∴x= 是增根,舍去.
解方程:
x(x-2)
解:方程两边同乘以最简公分母 ,
x 2+ x -6=0
化简,得
解得 x1= x2=
检验:把x1= 代入最简公分母, x(x-2)≠0;
把x2= 代入最简公分母, x(x-2)=0
∴原方程的根是x=
2
-3
-3
2
2
-3
解方程
解:原方程可化为
两边都乘以
得
化简整理得
解得
∴经检验:
是原方程的解
还有其它方法吗?
例题欣赏
解:原方程可化为
,方程化为
解得
可设
当
即
解得:
当
即
此方程无解
∴经检验:
是原方程的解
例题欣赏
特别提醒
知道了吗?
会用了吗?
掌握了吗?
象以上这种用一个字母(y) 来代替原方程中的一个较复杂的代数式 从而使原
方程简化,易于求解的方法,叫换元法
y
设 x2 + x =
y
y
下面的过程请同学们自己完成
相信你们能行
以下各方程能利用换元法进行换元吗?
能
不能
能
小结
有些分式方程用常规方法-----------去分母,是很复杂 ,甚至无法求解,有时要采取其他的方法
②各分式的分子、分母的次数相同,且相差一定的数,可将各分式拆成几项的和。这种解法称为 —— 拆 项 法
①采取局部通分法,会使解法很简单.这种解法称为 ——通 分 法
⑶用一个字母来代替原方程中的一个较复杂的代数式 ,从而使原方程简化,易于求解的方法,叫换元法
教师寄语
解分式方程的方法还很多,我们只讲了有限的一点,希望同学们课后自己去发现,相信同学们有更大的收获。
