人教版数学九年级上册 23.1旋转作图课件(共54张PPT)
文档属性
| 名称 | 人教版数学九年级上册 23.1旋转作图课件(共54张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 08:12:02 | ||
图片预览










文档简介
23.1 图形的旋转
情境问题
有三个著名演员应邀到同一个剧场参加同台演出,三个演员给剧场经理提了同一个条件:在同一张宣传海报上要把他们的名字都排在第一位,否则他们就退出演出。经理沉思了一会儿笑着答应了他们的要求。聪明的同学们,你们知道经理用的是什么办法吗?
都围绕着一个固定点转动,整个转动过程中,图形的形状、大小没有发生改变。
23.1 图形的旋转
1.理解旋转的有关概念及旋转的要素。
2.探究和发现旋转的基本性质。
3.能利用旋转知识解决简单的数学问题。
一、 学习 目标
二、学习重点: 旋转的有关概念和旋转的基本性质。
三、学习难点: 探索旋转的基本性质。
1.理解旋转的有关概念及旋转的要素。
2.探究和发现旋转的基本性质。
3.能利用旋转知识解决简单的数学问题。
一、 学习 目标
二、学习重点: 旋转的有关概念和旋转的基本性质。
三、学习难点: 探索旋转的基本性质。
什么叫图形的旋转、旋转中心、旋转角、旋转的对应点?确定图形的旋转有几要素?
(2分钟内完成)
自学指导:自学教材第59页内容,完成下列问题:
一、自主学习
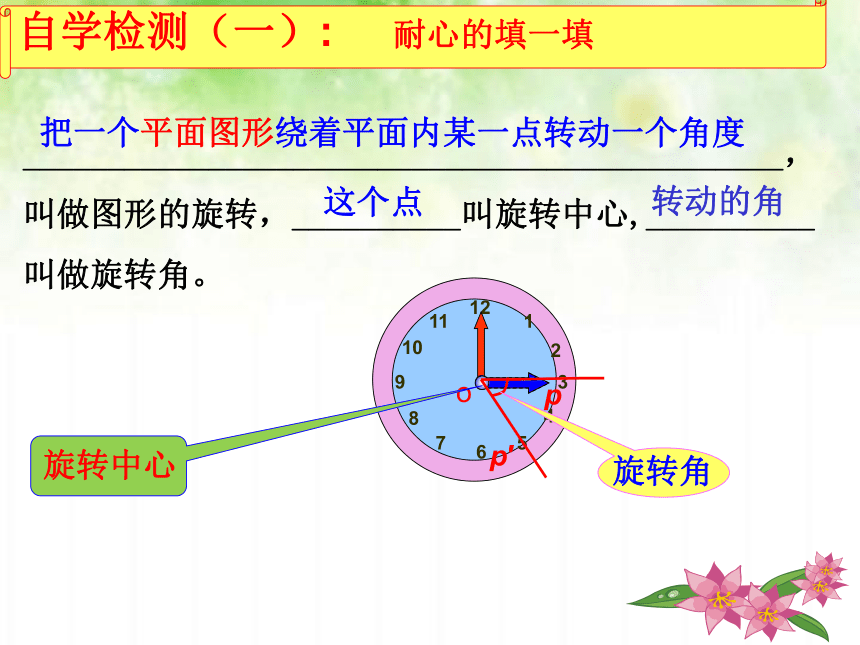
_____________________________________________,叫做图形的旋转,__________叫旋转中心,__________叫做旋转角。
把一个平面图形绕着平面内某一点转动一个角度
12
6
1
2
3
4
5
7
8
9
10
11
o
p
p′
转动的角
这个点
自学检测(一): 耐心的填一填
旋转中心
旋转角
________________________________________________________叫做旋转的对应点。
图形上的某个点经过旋转后得到一个新的点,这两个点
确定旋转的要素有_____________________________。
旋转中心和旋转角(旋转方向)
B
A
C
O
D
E
F
自学检测二 我聪明,我知道
1、下列现象中属于旋转的有( )个.
①火车行驶; ④钟摆的运动;
②荡秋千运动; ⑤圆规画圆.
③汽车方向盘的转动;
A. 1 B. 2 C. 3 D. 4
D
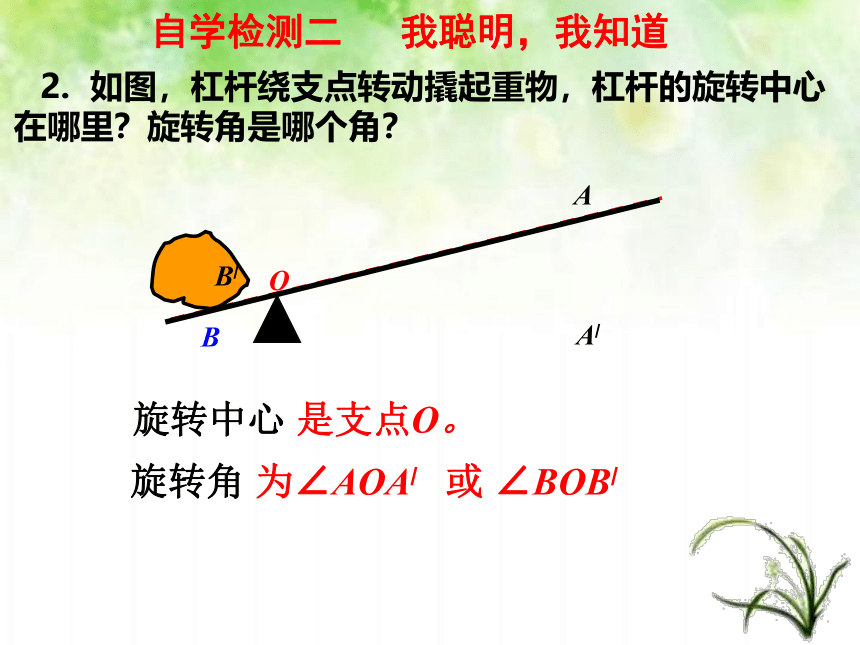
2. 如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
B
O
B/
A
A/
旋转中心 是支点O。
旋转角 为∠AOA/ 或 ∠BOB/
自学检测二 我聪明,我知道
在硬纸板上挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案△ABC,然后围绕旋转中心转动硬纸板,再描出这个挖掉的△A′B′C′ ,移开硬纸板。
大家一起来 学习真愉快
将△ABC绕点O 顺时针旋转到△A′B′C′的位置,连接三角形个顶点于旋转中心O,发现其中的道理。
二、合作探究: 图形的旋转有哪些性质?
B'
A'
C'
B
O
A
C
B
O
A
C
B
O
A
C
O
C
B/
A/
A
B
C/
C
O
B/
A/
A
B
C/
C
O
2.度量AO与A/O、BO与B/O、CO与C/O的长度,你发现了什么?
3.要想知道△ABC旋转的角度,我可以测量哪些角?
实践出真知
1、猜想:旋转前后两个三角形大小关系如何?
1、旋转前后两个三角形全等。
2.对应点到旋转中心的距离相等;
3.对应点与旋转中心所连线段的夹角等于旋转角.
概括结论,揭示性质:
对应点与旋转中心所连线段的夹角等于旋转角.
归
纳
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
旋转的性质:
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE旋转90°,画出旋转后的图形。
想一想:有几种作法?
A
D
E
C
B
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
知识升华
利用旋转来解决数学问题
学习反思
谈谈这节课你有什收获,还有什么疑惑?
课外作业
教材第61页练习题第2题。
愿你用勤奋的汗水
浇灌智慧的花朵!
教师寄语
今日作业
教材61页
练习题第1题
感谢各位专家评委老师的光临指导
大家辛苦了
1.如图,小明坐在秋千上,秋千旋转了80°,请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.
P
P′
知识升华
利用旋转来解决数学问题
(第5题)
2.如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.
A
60
等边
2.如图,用左面的三角形经过怎样的旋转,可以得到右面的图形?
3.找出图中扳手拧螺母时的旋转中心和旋转角.
O
旋转中心为螺母的中心O
旋转角为∠POP′
P
P′
1.如图,小明坐在秋千上,秋千旋转了80°。请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.
随堂练习
2.如图,用左面的三角形经过怎样旋转,可以得到右面的图形.
3.找出图中扳手拧螺母时的旋转中心和旋转角.
随堂练习
时针的端点在3时的位置P与在5时的位置P′是对应点.
12
6
1
2
3
4
5
7
8
9
10
11
P
P′
1.如图,从3时到5时,时针在转动的过程中, 旋转中心是什么?旋转角度是多少?对应点是什么?
表盘的中心是旋转中心
旋转角是60°
基本练习
三;
A
O
例1 将A点绕O点沿顺时针方向旋转60?.
作法:
1.连接OA,以点O为顶点,OA为边,作∠AOM =60?
A’
点的旋转作法
1、定好旋转中心
2、认准旋转方向
3、确定旋转角度
M
2. OM上取OB=OA, 点A’即为点A旋转后的对应点。
A
O
例2 将线段AB绕O点沿顺时针方向旋转60?.
作法:
将点A绕点O顺时针旋转60?,得 点A`;
2. 将点B绕点O顺时针旋转60 ?,得点B` ;
3. 连接A`B`, 则线段A`B`即为所求.
A`
B
B`
线段的旋转作法
1、定好旋转中心
2、认准旋转方向
3、确定旋转角度
例题3:如图: O是△ABC外一点,以O为旋转中心,将△ABC按顺时针方向旋转60?
C
A
B
O
A`
B`
C`
在这个旋转过程中:
旋转中心是____;A的对应点
___, B的对应点___,
C的对应点___.
OA____OA`;OB____OB`
OC____OC`. ∠ AOA`=___,
∠ BOB`=___,∠COC`=___.
图形的旋转作法
下图由四部分组成,每部分都包括两个小“十字”。红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他的方式吗?
12
6
1
2
3
4
5
7
8
9
10
11
o
自学检测(一)
2、图中时针的转动、风车叶片的转动等现象有什么共同的特征?
都围绕着一个定点转动,整个转动过程中,
形状、大小没有发生改变。
1、钟表的指针在不停地转动,从3时动到5时,时针旋转了多少度?
时针旋转了60°。
旋转
B'
A'
C'
B
O
A
C
B
O
A
C
B
O
A
C
O
C
平移
先平移后旋转
轴对称后旋转
12
6
1
2
3
4
5
7
8
9
10
11
o
聪明的同学们,你们能告诉我,这些物体的运动方式是一种什么运动吗?这些运动方式有什么共同特征?
钟表上的时针从3时到5时,时针走了多少度?
风车风轮的每个叶片在风的吹动下运动到新的位置,
1、课本p66页第1、4题
2、请设计一个绕一点旋转600后能与自身重合的图形.
作业
3. 如图:?ABC是等边三角形,D是BC上一点, ?ABD经过 旋转后到达?ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?
E
D
C
B
A
M
.
解:(1)旋转中心是A;
(2)旋转了60度;
(3)点M转到了AC的中点位置上.
二、议一议
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF。在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移到什么位置?
(3)AO与DO的长有什么关系?BO与EO呢?
(4)∠AOD与∠BOE有什么大小关系?
对比平移、轴对称两种变换,旋转变换与另两种变换有哪些共性与区别?
形状
大小
方向
轴对称
不变
不变
改变
平移
不变
不变
不变
旋转
不变
不变
改变
三种图形变换都是全等变换
小结
再 见
谢谢专家和老师们的指导!
2.时钟的时针在不停地旋转,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?
12
6
1
2
3
4
5
7
8
9
10
11
12
6
1
2
3
4
5
7
8
9
10
11
旋转角度是90°
旋转角度是30°
3. 如图,杠杆绕支点转动撬起重物,杠杆的旋转
中心在哪里?旋转角是哪个角?
B
O
B/
A
A/
旋转中心在支点O
旋转角为∠AOA/
或∠BOB/
实践探究
在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A′B′C′) ,移开硬纸板.
线段OA与OA′有什么关系?∠AOA′与∠BOB′有什么关系? △ABC与△A′B′C′形状和大小有什么关系?
A
B
C
O
A′
B′
C′
活动1
OA=OA′
∠AOA′=∠BOB′
△ABC≌△A′B′C′
对应点与旋转中心所连线段的夹角等于旋转角.
归
纳
活动2
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
2.举出一些生活中属于旋转的实例,并指出旋转中心和旋转角。
自学检测二 我聪明,我知道
随堂练习
3.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?
随堂练习
4.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
A
B
C
D
E
E′
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
关键:确定△ADE三个顶点的对应点,即它们旋转后的位置.
例题赏析
还有别的办法吗?
利用旋转来解决数学问题
情境问题
有三个著名演员应邀到同一个剧场参加同台演出,三个演员给剧场经理提了同一个条件:在同一张宣传海报上要把他们的名字都排在第一位,否则他们就退出演出。经理沉思了一会儿笑着答应了他们的要求。聪明的同学们,你们知道经理用的是什么办法吗?
都围绕着一个固定点转动,整个转动过程中,图形的形状、大小没有发生改变。
23.1 图形的旋转
1.理解旋转的有关概念及旋转的要素。
2.探究和发现旋转的基本性质。
3.能利用旋转知识解决简单的数学问题。
一、 学习 目标
二、学习重点: 旋转的有关概念和旋转的基本性质。
三、学习难点: 探索旋转的基本性质。
1.理解旋转的有关概念及旋转的要素。
2.探究和发现旋转的基本性质。
3.能利用旋转知识解决简单的数学问题。
一、 学习 目标
二、学习重点: 旋转的有关概念和旋转的基本性质。
三、学习难点: 探索旋转的基本性质。
什么叫图形的旋转、旋转中心、旋转角、旋转的对应点?确定图形的旋转有几要素?
(2分钟内完成)
自学指导:自学教材第59页内容,完成下列问题:
一、自主学习
_____________________________________________,叫做图形的旋转,__________叫旋转中心,__________叫做旋转角。
把一个平面图形绕着平面内某一点转动一个角度
12
6
1
2
3
4
5
7
8
9
10
11
o
p
p′
转动的角
这个点
自学检测(一): 耐心的填一填
旋转中心
旋转角
________________________________________________________叫做旋转的对应点。
图形上的某个点经过旋转后得到一个新的点,这两个点
确定旋转的要素有_____________________________。
旋转中心和旋转角(旋转方向)
B
A
C
O
D
E
F
自学检测二 我聪明,我知道
1、下列现象中属于旋转的有( )个.
①火车行驶; ④钟摆的运动;
②荡秋千运动; ⑤圆规画圆.
③汽车方向盘的转动;
A. 1 B. 2 C. 3 D. 4
D
2. 如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
B
O
B/
A
A/
旋转中心 是支点O。
旋转角 为∠AOA/ 或 ∠BOB/
自学检测二 我聪明,我知道
在硬纸板上挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案△ABC,然后围绕旋转中心转动硬纸板,再描出这个挖掉的△A′B′C′ ,移开硬纸板。
大家一起来 学习真愉快
将△ABC绕点O 顺时针旋转到△A′B′C′的位置,连接三角形个顶点于旋转中心O,发现其中的道理。
二、合作探究: 图形的旋转有哪些性质?
B'
A'
C'
B
O
A
C
B
O
A
C
B
O
A
C
O
C
B/
A/
A
B
C/
C
O
B/
A/
A
B
C/
C
O
2.度量AO与A/O、BO与B/O、CO与C/O的长度,你发现了什么?
3.要想知道△ABC旋转的角度,我可以测量哪些角?
实践出真知
1、猜想:旋转前后两个三角形大小关系如何?
1、旋转前后两个三角形全等。
2.对应点到旋转中心的距离相等;
3.对应点与旋转中心所连线段的夹角等于旋转角.
概括结论,揭示性质:
对应点与旋转中心所连线段的夹角等于旋转角.
归
纳
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
旋转的性质:
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE旋转90°,画出旋转后的图形。
想一想:有几种作法?
A
D
E
C
B
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
A
D
E
知识升华
利用旋转来解决数学问题
学习反思
谈谈这节课你有什收获,还有什么疑惑?
课外作业
教材第61页练习题第2题。
愿你用勤奋的汗水
浇灌智慧的花朵!
教师寄语
今日作业
教材61页
练习题第1题
感谢各位专家评委老师的光临指导
大家辛苦了
1.如图,小明坐在秋千上,秋千旋转了80°,请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.
P
P′
知识升华
利用旋转来解决数学问题
(第5题)
2.如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.
A
60
等边
2.如图,用左面的三角形经过怎样的旋转,可以得到右面的图形?
3.找出图中扳手拧螺母时的旋转中心和旋转角.
O
旋转中心为螺母的中心O
旋转角为∠POP′
P
P′
1.如图,小明坐在秋千上,秋千旋转了80°。请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.
随堂练习
2.如图,用左面的三角形经过怎样旋转,可以得到右面的图形.
3.找出图中扳手拧螺母时的旋转中心和旋转角.
随堂练习
时针的端点在3时的位置P与在5时的位置P′是对应点.
12
6
1
2
3
4
5
7
8
9
10
11
P
P′
1.如图,从3时到5时,时针在转动的过程中, 旋转中心是什么?旋转角度是多少?对应点是什么?
表盘的中心是旋转中心
旋转角是60°
基本练习
三;
A
O
例1 将A点绕O点沿顺时针方向旋转60?.
作法:
1.连接OA,以点O为顶点,OA为边,作∠AOM =60?
A’
点的旋转作法
1、定好旋转中心
2、认准旋转方向
3、确定旋转角度
M
2. OM上取OB=OA, 点A’即为点A旋转后的对应点。
A
O
例2 将线段AB绕O点沿顺时针方向旋转60?.
作法:
将点A绕点O顺时针旋转60?,得 点A`;
2. 将点B绕点O顺时针旋转60 ?,得点B` ;
3. 连接A`B`, 则线段A`B`即为所求.
A`
B
B`
线段的旋转作法
1、定好旋转中心
2、认准旋转方向
3、确定旋转角度
例题3:如图: O是△ABC外一点,以O为旋转中心,将△ABC按顺时针方向旋转60?
C
A
B
O
A`
B`
C`
在这个旋转过程中:
旋转中心是____;A的对应点
___, B的对应点___,
C的对应点___.
OA____OA`;OB____OB`
OC____OC`. ∠ AOA`=___,
∠ BOB`=___,∠COC`=___.
图形的旋转作法
下图由四部分组成,每部分都包括两个小“十字”。红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他的方式吗?
12
6
1
2
3
4
5
7
8
9
10
11
o
自学检测(一)
2、图中时针的转动、风车叶片的转动等现象有什么共同的特征?
都围绕着一个定点转动,整个转动过程中,
形状、大小没有发生改变。
1、钟表的指针在不停地转动,从3时动到5时,时针旋转了多少度?
时针旋转了60°。
旋转
B'
A'
C'
B
O
A
C
B
O
A
C
B
O
A
C
O
C
平移
先平移后旋转
轴对称后旋转
12
6
1
2
3
4
5
7
8
9
10
11
o
聪明的同学们,你们能告诉我,这些物体的运动方式是一种什么运动吗?这些运动方式有什么共同特征?
钟表上的时针从3时到5时,时针走了多少度?
风车风轮的每个叶片在风的吹动下运动到新的位置,
1、课本p66页第1、4题
2、请设计一个绕一点旋转600后能与自身重合的图形.
作业
3. 如图:?ABC是等边三角形,D是BC上一点, ?ABD经过 旋转后到达?ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?
E
D
C
B
A
M
.
解:(1)旋转中心是A;
(2)旋转了60度;
(3)点M转到了AC的中点位置上.
二、议一议
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF。在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移到什么位置?
(3)AO与DO的长有什么关系?BO与EO呢?
(4)∠AOD与∠BOE有什么大小关系?
对比平移、轴对称两种变换,旋转变换与另两种变换有哪些共性与区别?
形状
大小
方向
轴对称
不变
不变
改变
平移
不变
不变
不变
旋转
不变
不变
改变
三种图形变换都是全等变换
小结
再 见
谢谢专家和老师们的指导!
2.时钟的时针在不停地旋转,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?
12
6
1
2
3
4
5
7
8
9
10
11
12
6
1
2
3
4
5
7
8
9
10
11
旋转角度是90°
旋转角度是30°
3. 如图,杠杆绕支点转动撬起重物,杠杆的旋转
中心在哪里?旋转角是哪个角?
B
O
B/
A
A/
旋转中心在支点O
旋转角为∠AOA/
或∠BOB/
实践探究
在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A′B′C′) ,移开硬纸板.
线段OA与OA′有什么关系?∠AOA′与∠BOB′有什么关系? △ABC与△A′B′C′形状和大小有什么关系?
A
B
C
O
A′
B′
C′
活动1
OA=OA′
∠AOA′=∠BOB′
△ABC≌△A′B′C′
对应点与旋转中心所连线段的夹角等于旋转角.
归
纳
活动2
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
2.举出一些生活中属于旋转的实例,并指出旋转中心和旋转角。
自学检测二 我聪明,我知道
随堂练习
3.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?
随堂练习
4.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
A
B
C
D
E
E′
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
关键:确定△ADE三个顶点的对应点,即它们旋转后的位置.
例题赏析
还有别的办法吗?
利用旋转来解决数学问题
同课章节目录
