人教版数学九年级上册23.2.1中心对称课件(共28张PPT)
文档属性
| 名称 | 人教版数学九年级上册23.2.1中心对称课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 00:00:00 | ||
图片预览







文档简介
23.2 中心对称
北京国家大剧院
性质:
1.成轴对称的两个图形全等
2.对称点的连线被对称轴垂直平分
3.轴对称变换是空间内图形的全等变换
定义:如果把一个图形沿某一条直线折叠, 能与另一个图形重合,那么叫做
这两个图形关于这条直线成轴对称。
轴对称
复习整理:
新疆达坂城风力发电站
旋转的要素: 1. 旋转中心
2. 旋转角
3.旋转方向
旋转变换是平面内图形的全等变换
复习整理:
太极图
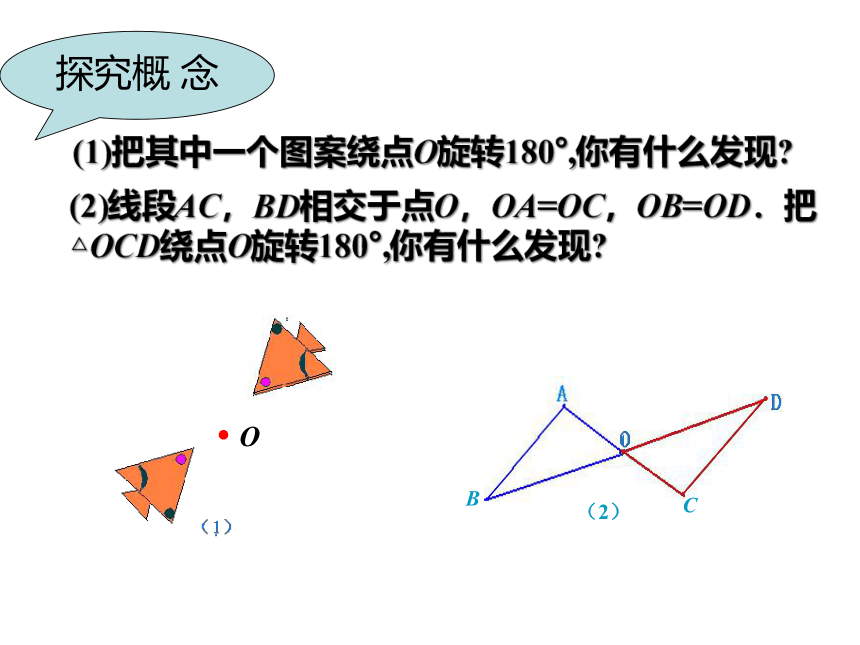
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现?
O
C
B
(2)
探究概 念
把一个图形绕着某一个点旋转180°,如果它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
C
B
△OCD和△OAB关于
对称,对称点是 .
点O
点A和C,B和D
明确概 念
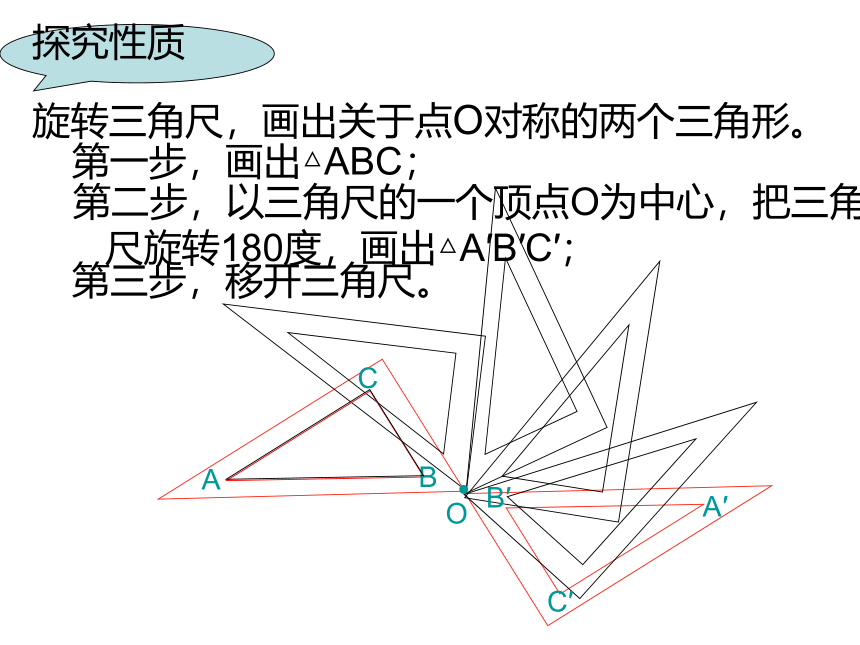
旋转三角尺,画出关于点O对称的两个三角形。
第一步,画出△ABC;
第二步,以三角尺的一个顶点O为中心,把三角尺旋转180度,画出△A′B′C′;
第三步,移开三角尺。
A′
C
A
B
B′
C′
O
●
探究性质
探究:1.分别连接对称点AA′,BB′,CC′。
点O在线段AA′上吗?如果在,在什么位置?
O
●
A′
C′
B′
C
A
B
2.△ABC与△A′B′C′全等吗?为什么?
3.你能从中得到什么结论?
探究性质:
O
●
A′
C′
B′
C
A
B
1、中心对称的两个图形,对称点所连线段经过对称中心,而且被对称中心所平分。
2、中心对称的两个图形是全等形。
归纳性质
中心对称与轴对称有什么区别?又有什么联系?
轴对称
中心对称
有一条对称轴——直线
图形沿对称轴对折(翻折180°)后重合
(空间内全等变换 )
对称点的连线被对称轴垂直平分
有一个对称中心——点
图形绕对称中心旋转180°后重合
(平面内全等变换)
对称点连线经过对称中心,且被对称中心平分
A
O
A′
例1 (1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;
则点A′即为所求的点.
画法:连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.
尝试运用
例1 (2)如图,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
则△A′B′C′即为所求的三角形。
尝试运用
(1)画一个点关于某点(对称中心)的对称点的画法是:先连接这个点与对称中心并延长一倍即可.
(2)画一个图形关于某点的对称图形的画法是:先画出图形中的几个特殊点关于某点的对称点,然后再顺次连结有关对称点即可.
作图归纳:
双基演练:
已知四边形ABCD和画四边A′B′C′D′成中心对称 ,试确定它们的对称中心O 。
A
B
A’
C’
B’
D’
D
O
C
则点O即为所求的图形。
逆向思考:
1.下面五组图形中,左边的图形与右边的图形成中心对称的有( )
1.性质1反过来,即如果两个图形的对应点连线都经过某一点,并且被这点平分,那么这两个图形是否关于这一点对称?
2.性质2反过来,即两个全等的图形是中心对称的,对吗?
逆向思考:
小结反思
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
1、必做题:教科书第67页第1题。
2、选做题:做一个风车
精选作业:
1.(湖南长沙)在下面的格点图中,每个小正方形的边长均为1个单位,请按下列要求画出图形:
(1)画出图①中阴影部分关于O点的中心对称图形;
(2)画出图②中阴影部分向右平移9个单位后的图形;
(3)画出图③中阴影部分关于直线AB的轴对称图形.
(图①) (图②) (图③)
聚焦中考:
2.如图,等腰梯形ABCD中,AD∥BC,AB=CD,且
AD= BC=2cm,E是BC的中点,则△ABE可以看成
是由△DEC向左平移而得到,平移的距离为_______;
而△AED与△CDE是成中心对称的两个三角形,
它们的对称中心是________.
3、如下图,点A、B为河塘两对岸的两座村庄,为了测量两村庄间的距离,因条件限制,不能经过河塘直接测量。请你想一想,能否利用所学的知识来解决这个问题呢?
A
B
拓展应用
解答:由于测量时不能经过河塘,这就需要将两点
(村庄)在不改变AB两点之间的距离的情况下,移 动到适当位置。首先在河塘岸边适当的位置取一点C
(如下图),连接AC、BC(使保持AC、BC不经过河 塘),分别将AC、BC延长到点A’、B’,使A’C?AC, B’C?BC;这样即是作线段AB关于点C的中心对
称图形A’B’,根据中心对称的特征有
A’B’?AB,所以测出A’、B’两点间的距
离,就是A、B两点间的距离,也即两
村庄间的距离。
A
B
C
A’
B’
2、画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点O为对称中心。
提高练习
D
A
B
C
E
F
G
M
D
A
B
C
O
.
N
谢谢
你用什么方法识别两个图形是否关于某点中心对称?
方法1:定义
方法2:如果两个图形的对应点连成的线段
都经过某一点,并且都被该点平分,
那么这两个图形一定关于这一点
成中心对称.
深入理解:
北京国家大剧院
性质:
1.成轴对称的两个图形全等
2.对称点的连线被对称轴垂直平分
3.轴对称变换是空间内图形的全等变换
定义:如果把一个图形沿某一条直线折叠, 能与另一个图形重合,那么叫做
这两个图形关于这条直线成轴对称。
轴对称
复习整理:
新疆达坂城风力发电站
旋转的要素: 1. 旋转中心
2. 旋转角
3.旋转方向
旋转变换是平面内图形的全等变换
复习整理:
太极图
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现?
O
C
B
(2)
探究概 念
把一个图形绕着某一个点旋转180°,如果它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
C
B
△OCD和△OAB关于
对称,对称点是 .
点O
点A和C,B和D
明确概 念
旋转三角尺,画出关于点O对称的两个三角形。
第一步,画出△ABC;
第二步,以三角尺的一个顶点O为中心,把三角尺旋转180度,画出△A′B′C′;
第三步,移开三角尺。
A′
C
A
B
B′
C′
O
●
探究性质
探究:1.分别连接对称点AA′,BB′,CC′。
点O在线段AA′上吗?如果在,在什么位置?
O
●
A′
C′
B′
C
A
B
2.△ABC与△A′B′C′全等吗?为什么?
3.你能从中得到什么结论?
探究性质:
O
●
A′
C′
B′
C
A
B
1、中心对称的两个图形,对称点所连线段经过对称中心,而且被对称中心所平分。
2、中心对称的两个图形是全等形。
归纳性质
中心对称与轴对称有什么区别?又有什么联系?
轴对称
中心对称
有一条对称轴——直线
图形沿对称轴对折(翻折180°)后重合
(空间内全等变换 )
对称点的连线被对称轴垂直平分
有一个对称中心——点
图形绕对称中心旋转180°后重合
(平面内全等变换)
对称点连线经过对称中心,且被对称中心平分
A
O
A′
例1 (1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;
则点A′即为所求的点.
画法:连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.
尝试运用
例1 (2)如图,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
则△A′B′C′即为所求的三角形。
尝试运用
(1)画一个点关于某点(对称中心)的对称点的画法是:先连接这个点与对称中心并延长一倍即可.
(2)画一个图形关于某点的对称图形的画法是:先画出图形中的几个特殊点关于某点的对称点,然后再顺次连结有关对称点即可.
作图归纳:
双基演练:
已知四边形ABCD和画四边A′B′C′D′成中心对称 ,试确定它们的对称中心O 。
A
B
A’
C’
B’
D’
D
O
C
则点O即为所求的图形。
逆向思考:
1.下面五组图形中,左边的图形与右边的图形成中心对称的有( )
1.性质1反过来,即如果两个图形的对应点连线都经过某一点,并且被这点平分,那么这两个图形是否关于这一点对称?
2.性质2反过来,即两个全等的图形是中心对称的,对吗?
逆向思考:
小结反思
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
1、必做题:教科书第67页第1题。
2、选做题:做一个风车
精选作业:
1.(湖南长沙)在下面的格点图中,每个小正方形的边长均为1个单位,请按下列要求画出图形:
(1)画出图①中阴影部分关于O点的中心对称图形;
(2)画出图②中阴影部分向右平移9个单位后的图形;
(3)画出图③中阴影部分关于直线AB的轴对称图形.
(图①) (图②) (图③)
聚焦中考:
2.如图,等腰梯形ABCD中,AD∥BC,AB=CD,且
AD= BC=2cm,E是BC的中点,则△ABE可以看成
是由△DEC向左平移而得到,平移的距离为_______;
而△AED与△CDE是成中心对称的两个三角形,
它们的对称中心是________.
3、如下图,点A、B为河塘两对岸的两座村庄,为了测量两村庄间的距离,因条件限制,不能经过河塘直接测量。请你想一想,能否利用所学的知识来解决这个问题呢?
A
B
拓展应用
解答:由于测量时不能经过河塘,这就需要将两点
(村庄)在不改变AB两点之间的距离的情况下,移 动到适当位置。首先在河塘岸边适当的位置取一点C
(如下图),连接AC、BC(使保持AC、BC不经过河 塘),分别将AC、BC延长到点A’、B’,使A’C?AC, B’C?BC;这样即是作线段AB关于点C的中心对
称图形A’B’,根据中心对称的特征有
A’B’?AB,所以测出A’、B’两点间的距
离,就是A、B两点间的距离,也即两
村庄间的距离。
A
B
C
A’
B’
2、画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点O为对称中心。
提高练习
D
A
B
C
E
F
G
M
D
A
B
C
O
.
N
谢谢
你用什么方法识别两个图形是否关于某点中心对称?
方法1:定义
方法2:如果两个图形的对应点连成的线段
都经过某一点,并且都被该点平分,
那么这两个图形一定关于这一点
成中心对称.
深入理解:
同课章节目录
