六年级上册数学讲义-小升初培优:第02讲幻方(解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义-小升初培优:第02讲幻方(解析版)全国通用 |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 08:01:03 | ||
图片预览


文档简介
第二讲 幻方
请将2009、2010、2011、2012、2013、2014、2015、2016、2017这9个自然数填入图中的空格内,使每行、每列、两条对角线上的3个数之和相等。(只要构造出一种)
【解析】方法一:
第一步——求幻和:幻和为(2009+2010+2011+2012+2013+2014+2015+2016+2017)÷3=6039;
第二步——求中心数:中心数为6039÷3=2013;
第三步——确定4个角上的数:用尝试法,可推出4个角上的数只能为偶数;
第四步——求出幻方:根据幻和求出各边中点的数,求出1个基本解;以基本解为基础,可通过旋转或镜像变换得到其它各解,共8解。
答案如图所示。
方法二:与1-9的3阶幻方相比,每个空格上的数都增加2008;
根据1-9的3阶阶幻方的8个图可以求出原题的答案。答案如图所示。
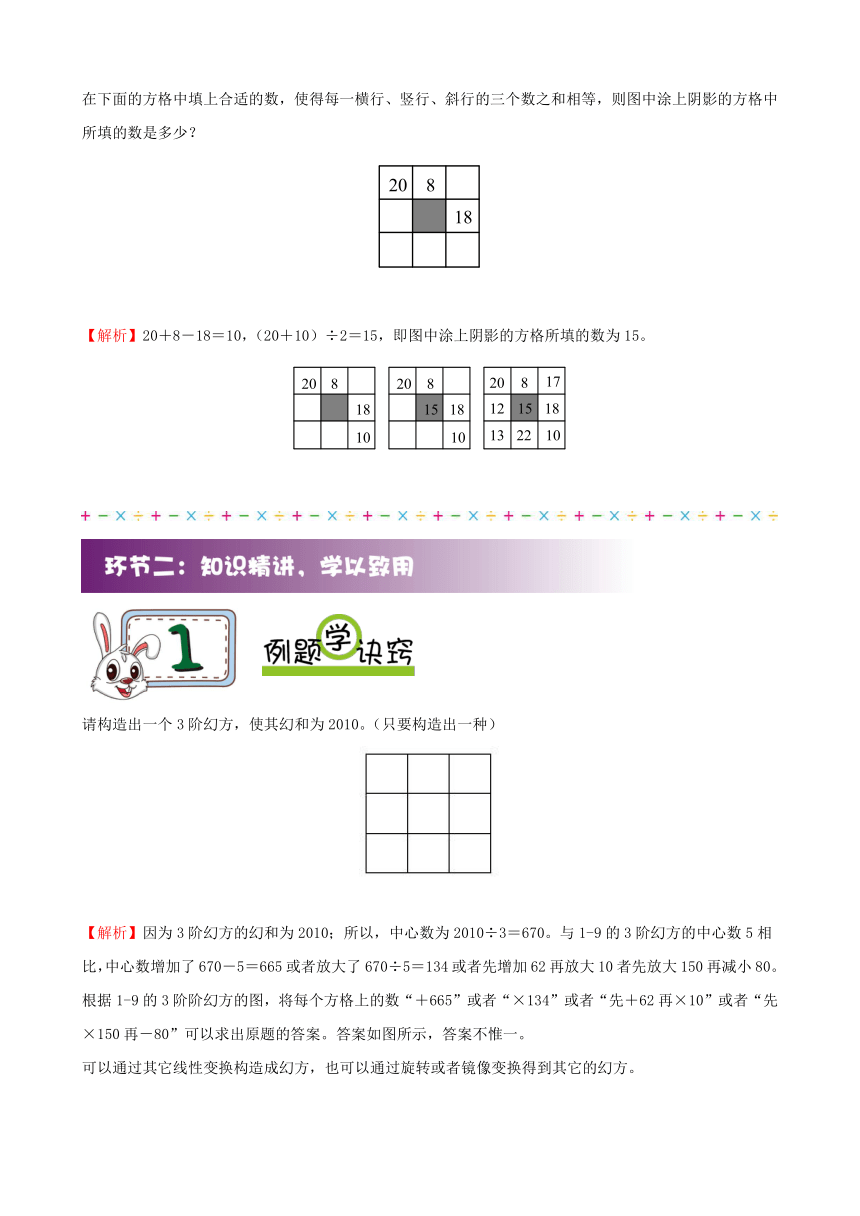
在下面的方格中填上合适的数,使得每一横行、竖行、斜行的三个数之和相等,则图中涂上阴影的方格中所填的数是多少?
【解析】20+8-18=10,(20+10)÷2=15,即图中涂上阴影的方格所填的数为15。
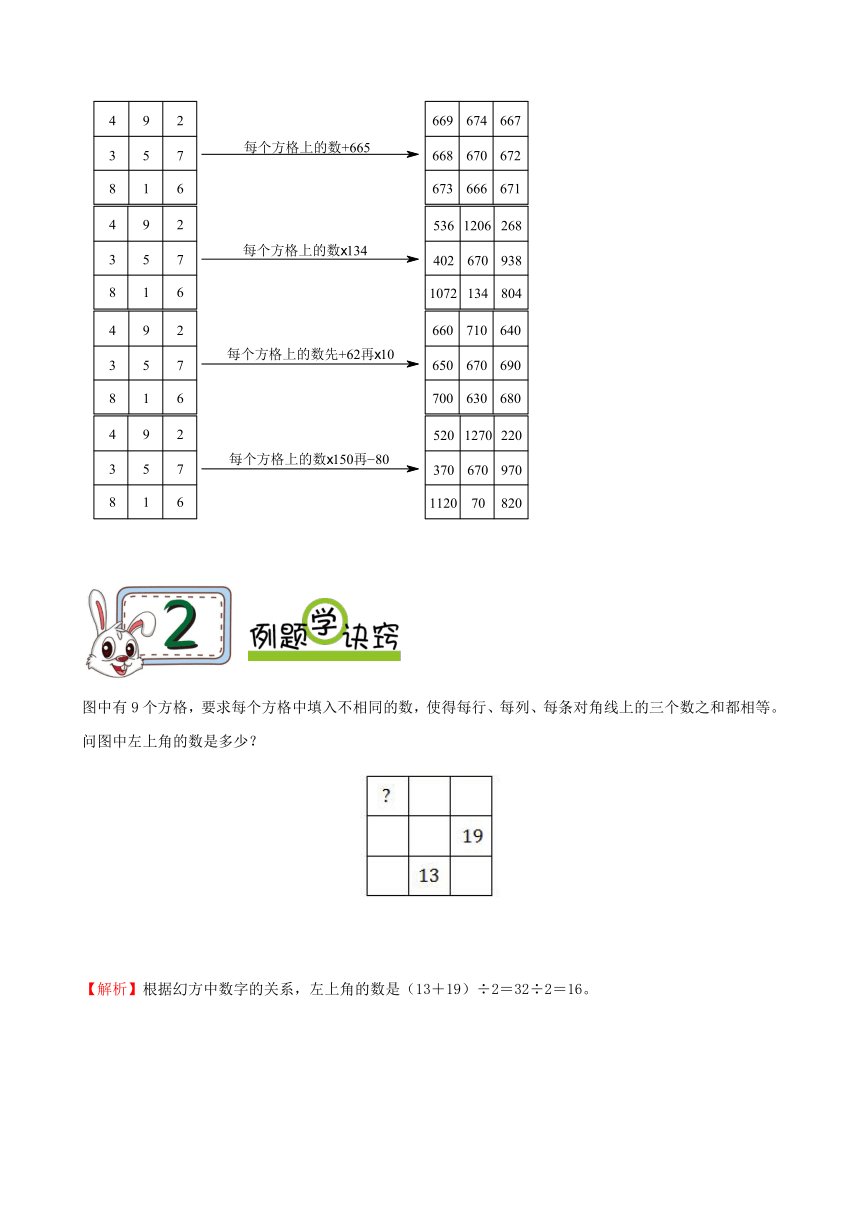
请构造出一个3阶幻方,使其幻和为2010。(只要构造出一种)
【解析】因为3阶幻方的幻和为2010;所以,中心数为2010÷3=670。与1-9的3阶幻方的中心数5相比,中心数增加了670-5=665或者放大了670÷5=134或者先增加62再放大10者先放大150再减小80。
根据1-9的3阶阶幻方的图,将每个方格上的数“+665”或者“×134”或者“先+62再×10”或者“先×150再-80”可以求出原题的答案。答案如图所示,答案不惟一。
可以通过其它线性变换构造成幻方,也可以通过旋转或者镜像变换得到其它的幻方。
图中有9个方格,要求每个方格中填入不相同的数,使得每行、每列、每条对角线上的三个数之和都相等。问图中左上角的数是多少?
【解析】根据幻方中数字的关系,左上角的数是(13+19)÷2=32÷2=16。
如图,用1-9这九个数字补全三阶幻方,并求出幻和是多少?
【解析】中心数为5,那么幻和为5×3=15。
在图的空格中填上不同的自然数,使每行、每列和两条对角线的四个数之和等于264,求A+B-C+D+E-F+G-H的结果是多少?
【解析】填数,四阶幻方。A+B-C+D+E-F+G-H=16。
把1-9九个数分别填入如图所示的九个小圆圈内,使图中的大小六个圆,每个圆上的数字和相等。
【解析】填数,数阵图。因为4小圆上的数字和相等;所以4小圆上除去中间的小圆圈内的数字其它3个小圆圈内的数字和相等;(相等于三阶幻方中有2行、2列上的数相等)所以本题的解题思路实际上是三阶幻方(九宫格)的变形,如图一所示为一个三阶幻方;如图二所示是将这个三阶幻方变形的数阵图。
如图,要在下面的空格中填入适当的数,使每行、每列及对角线的3个数之和都相等,问号处应填入的数。要求写出关键的解题推理过程。
【解析】中心数=(6+8)÷2=7。
如图所示,9个小正方形内各填入一个有理数,使每行每列以及两条对角线上的三个有理数的和相等。现在58和152两个数已给出,那么“?”等于多少?
【解析】中心数=(58+152)÷2=105。
将11-19填入右图小方格里,使横行和竖列上五个数之和相等。
【解析】11+12+13+14+15+16+17+18+19=135,可见重叠数为奇数:11、13、15、17、19,那么可得答案如下图所示:
唐僧师徒摘桃子
一天,唐僧命徒弟悟空、八戒、沙僧三人去花果山摘些桃子。不长时间,徒弟三人摘完桃子高高兴兴回来。师父唐僧问:你们每人各摘回多少个桃子?
八戒憨笑着说:师父,我来考考你。我们每人摘的一样多,我筐里的桃子不到100个,如果3个3个地数,数到最后还剩1个。你算算,我们每人摘了多少个?
沙僧神秘地说:师父,我也来考考你。我筐里的桃子,如果4个4个地数,数到最后还剩1个。你算算,我们每人摘了多少个?
悟空笑眯眯地说:师父,我也来考考你。我筐里的_??????_,如果5个5个地数,数到最后还剩1个。你算算,我们每人摘多少个?
请将2009、2010、2011、2012、2013、2014、2015、2016、2017这9个自然数填入图中的空格内,使每行、每列、两条对角线上的3个数之和相等。(只要构造出一种)
【解析】方法一:
第一步——求幻和:幻和为(2009+2010+2011+2012+2013+2014+2015+2016+2017)÷3=6039;
第二步——求中心数:中心数为6039÷3=2013;
第三步——确定4个角上的数:用尝试法,可推出4个角上的数只能为偶数;
第四步——求出幻方:根据幻和求出各边中点的数,求出1个基本解;以基本解为基础,可通过旋转或镜像变换得到其它各解,共8解。
答案如图所示。
方法二:与1-9的3阶幻方相比,每个空格上的数都增加2008;
根据1-9的3阶阶幻方的8个图可以求出原题的答案。答案如图所示。
在下面的方格中填上合适的数,使得每一横行、竖行、斜行的三个数之和相等,则图中涂上阴影的方格中所填的数是多少?
【解析】20+8-18=10,(20+10)÷2=15,即图中涂上阴影的方格所填的数为15。
请构造出一个3阶幻方,使其幻和为2010。(只要构造出一种)
【解析】因为3阶幻方的幻和为2010;所以,中心数为2010÷3=670。与1-9的3阶幻方的中心数5相比,中心数增加了670-5=665或者放大了670÷5=134或者先增加62再放大10者先放大150再减小80。
根据1-9的3阶阶幻方的图,将每个方格上的数“+665”或者“×134”或者“先+62再×10”或者“先×150再-80”可以求出原题的答案。答案如图所示,答案不惟一。
可以通过其它线性变换构造成幻方,也可以通过旋转或者镜像变换得到其它的幻方。
图中有9个方格,要求每个方格中填入不相同的数,使得每行、每列、每条对角线上的三个数之和都相等。问图中左上角的数是多少?
【解析】根据幻方中数字的关系,左上角的数是(13+19)÷2=32÷2=16。
如图,用1-9这九个数字补全三阶幻方,并求出幻和是多少?
【解析】中心数为5,那么幻和为5×3=15。
在图的空格中填上不同的自然数,使每行、每列和两条对角线的四个数之和等于264,求A+B-C+D+E-F+G-H的结果是多少?
【解析】填数,四阶幻方。A+B-C+D+E-F+G-H=16。
把1-9九个数分别填入如图所示的九个小圆圈内,使图中的大小六个圆,每个圆上的数字和相等。
【解析】填数,数阵图。因为4小圆上的数字和相等;所以4小圆上除去中间的小圆圈内的数字其它3个小圆圈内的数字和相等;(相等于三阶幻方中有2行、2列上的数相等)所以本题的解题思路实际上是三阶幻方(九宫格)的变形,如图一所示为一个三阶幻方;如图二所示是将这个三阶幻方变形的数阵图。
如图,要在下面的空格中填入适当的数,使每行、每列及对角线的3个数之和都相等,问号处应填入的数。要求写出关键的解题推理过程。
【解析】中心数=(6+8)÷2=7。
如图所示,9个小正方形内各填入一个有理数,使每行每列以及两条对角线上的三个有理数的和相等。现在58和152两个数已给出,那么“?”等于多少?
【解析】中心数=(58+152)÷2=105。
将11-19填入右图小方格里,使横行和竖列上五个数之和相等。
【解析】11+12+13+14+15+16+17+18+19=135,可见重叠数为奇数:11、13、15、17、19,那么可得答案如下图所示:
唐僧师徒摘桃子
一天,唐僧命徒弟悟空、八戒、沙僧三人去花果山摘些桃子。不长时间,徒弟三人摘完桃子高高兴兴回来。师父唐僧问:你们每人各摘回多少个桃子?
八戒憨笑着说:师父,我来考考你。我们每人摘的一样多,我筐里的桃子不到100个,如果3个3个地数,数到最后还剩1个。你算算,我们每人摘了多少个?
沙僧神秘地说:师父,我也来考考你。我筐里的桃子,如果4个4个地数,数到最后还剩1个。你算算,我们每人摘了多少个?
悟空笑眯眯地说:师父,我也来考考你。我筐里的_??????_,如果5个5个地数,数到最后还剩1个。你算算,我们每人摘多少个?
同课章节目录
