六年级上册数学讲义-小升初培优:第04讲 三阶幻方 (解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义-小升初培优:第04讲 三阶幻方 (解析版)全国通用 |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 08:11:08 | ||
图片预览

文档简介
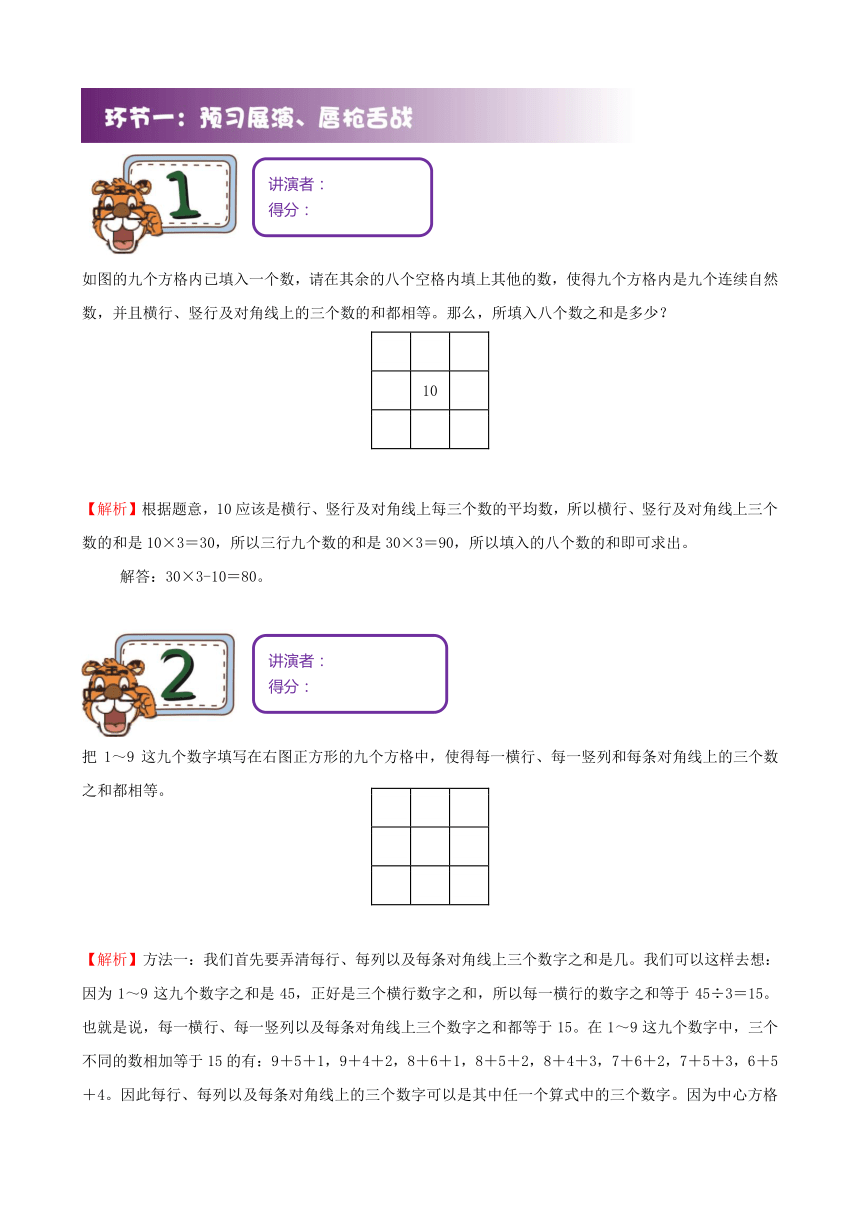
第四讲 三阶幻方
如图的九个方格内已填入一个数,请在其余的八个空格内填上其他的数,使得九个方格内是九个连续自然数,并且横行、竖行及对角线上的三个数的和都相等。那么,所填入八个数之和是多少?
? 10 ?
? ?
【解析】根据题意,10应该是横行、竖行及对角线上每三个数的平均数,所以横行、竖行及对角线上三个数的和是10×3=30,所以三行九个数的和是30×3=90,所以填入的八个数的和即可求出。
解答:30×3-10=80。
?
?
? ?
把1~9这九个数字填写在右图正方形的九个方格中,使得每一横行、每一竖列和每条对角线上的三个数之和都相等。
【解析】方法一:我们首先要弄清每行、每列以及每条对角线上三个数字之和是几。我们可以这样去想:因为1~9这九个数字之和是45,正好是三个横行数字之和,所以每一横行的数字之和等于45÷3=15。也就是说,每一横行、每一竖列以及每条对角线上三个数字之和都等于15。在1~9这九个数字中,三个不同的数相加等于15的有:9+5+1,9+4+2,8+6+1,8+5+2,8+4+3,7+6+2,7+5+3,6+5+4。因此每行、每列以及每条对角线上的三个数字可以是其中任一个算式中的三个数字。因为中心方格中的数既在一个横行中,又在一个竖列中,还在两对角线上,所以它应同时出现在上述的四个算式中,只有5符合条件,因此应将5填在中心方格中。同理,四个角上的数既在一个横行中,又在一个竖列中,还在一条对角线上,所以它应同时出现在上述的三个算式中,符合条件的有2,4,6,8,因此应将2,4,6,8填在四个角的方格中,同时应保证对角线两数的和相等。
方法二:九数斜排,四维突出,上下对调,左右对调。
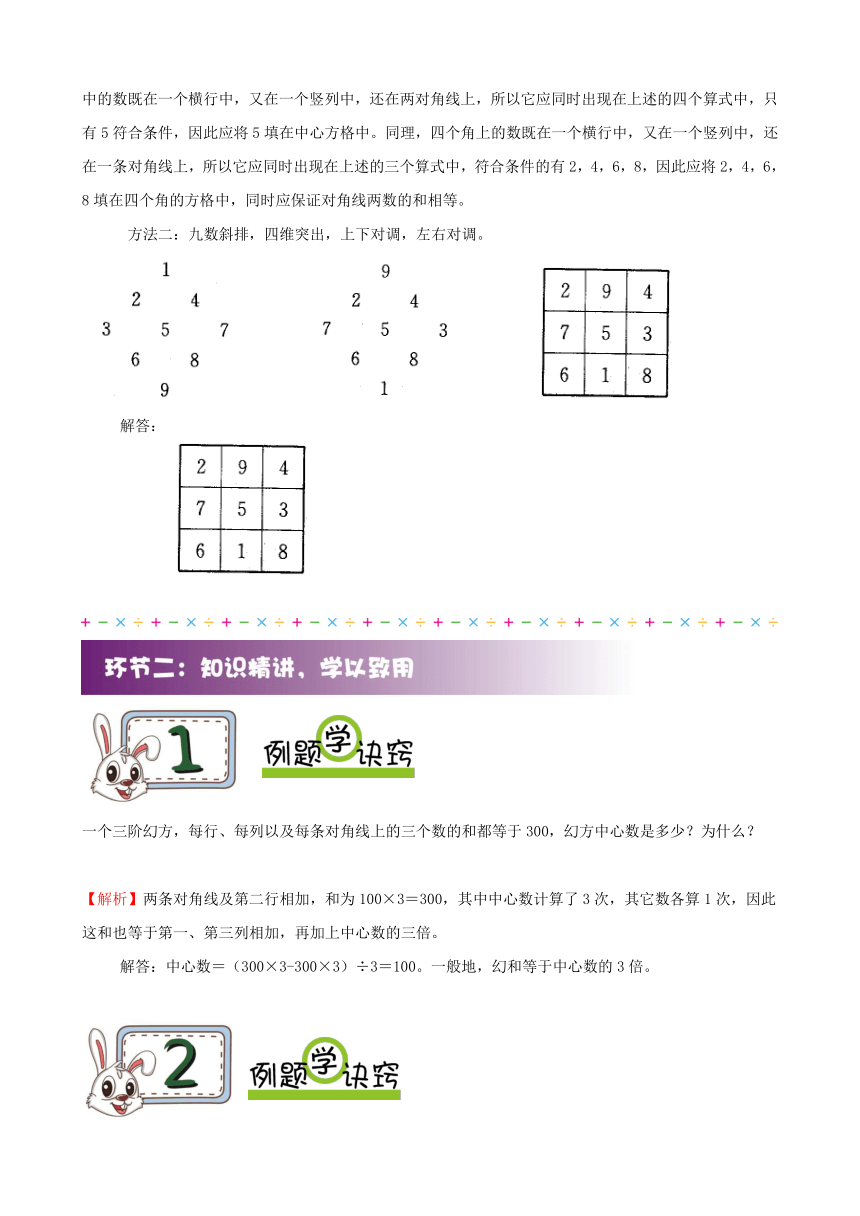
解答:
一个三阶幻方,每行、每列以及每条对角线上的三个数的和都等于300,幻方中心数是多少?为什么?
【解析】两条对角线及第二行相加,和为100×3=300,其中中心数计算了3次,其它数各算1次,因此这和也等于第一、第三列相加,再加上中心数的三倍。
解答:中心数=(300×3-300×3)÷3=100。一般地,幻和等于中心数的3倍。
在图中的每个空格内填入一个自然数,使得每一横行、每一竖列和每条对角线上的三个数之和都相等。这时右下角方格内的数与8,10有什么关系?
3 10
8
?
? ?
【解析】从左上到右下的对角线与第三行相加,和与第一、第二列相加的和相等,因此,右下角数的2倍等于8+10=18,右下角应填9。
解答:中心数等于(3+9)÷2=6。右下角数的2倍等于8+10=18。
如图,只能用图中已有的3个数填满其余的空格,并要求每个数字必须再使用2次,而且每行、每列及每条对角线上的3个数之和都相等。_???è??é?????_(1.31_KB)_
_???è??é?????_(1.74_KB)_
3 7
? 5 ?
? ?
' W& M; ~/ t( |
【解析】解答:
3 7 5
7 5 3
5 3 7
如图,在一个小方格里最多放入一个p,要想使得同一行、同一列或对角连线上的三个小方格最多不出现三个p,那么在这九个小方格里最多能放入多少个p?
?
?
? ?
p p
p
p
p p
【解析】因为每行每列不能出现3个p,且使九小方格里的p最多,所以每行每列都有2个p,只要保证正方形的对角线上的p不出现3个即可解答问题。
解答:如图2+2+2=6(个),九小方格里最多能放6个p。
如图,方格中横向、纵向和对角线方向的数字和都相等。那么填入4个角上的数字之和是多少?
4
? 4 ?
3
【解析】填入4个角上的数字之和是16。
解答:
3 5 4
5 4 3
4 3 5
如图:只能用图中已有的三个数字填满其中的空格,并要求每个数字必须使用3次,而且每行、每列及每条对角线上的三个数字之和都必须相等。
? ? 8
? 6 ?
4 ? ?
【解析】
6 4 8
8 6 4
4 8 6
解答:
把5~13九个数字填写在下图正方形的九个方格中,使得每一横行、每一竖列和每条对角线上的三个数之和都相等。
? ?
?
?
? ?
【解析】解答:
12 5 10
7 9 11
8 13 6
如图,老师将9个数写在一个九宫格里,让同学们选数,每个同学可以从中选出5个数来求和,小明选的5个数的和是120,小文选的5个数的和是111,如果他们选的数只有一个是一样的,那么这个数是多少?
11 12 13
21 22 23
31 32 33
【解析】因为两个人选的数只有一个是一样的,那么这两个人把表中的这9个数全部选到了,因此这个一样的数就是120+111-(11+12+13+21+22+23+31+32+32),解决问题。
120+111-(11+12+13+21+22+23+31+32+32)=231-198=33
解答:这个数是33。
华罗庚的故事
世界著名_??°??????_,_???????§????é??_院士,_?????????????§????é??_外籍院士,_?????????????§????é??é?????_,联邦德国巴伐利亚科学院院士。中国第一至_???????±???¨???????¤§????§????_委员。
他是中国_è§??????°è??_、矩阵几何学、_????????¤_、_è??????????°è??_与多元复变函数论等多方面研究的创始人和_??????è??_,也是中国在世界上最有_??±??????_的数学家之一,被列为_è?????????§????????????????é??_中当今世界88位数学_??????_之一。国际上以华氏命名的数学科研成果有“_????°???????_”、“华氏不等式”、“华—王方法”等。
在国际上以华氏命名的数学科研成果就有“华氏定理”、“怀依—华不等式”、“华氏不等式”、“普劳威尔—加当华定理”、“华氏算子”、“华—王方法”等。?
20世纪40年代,解决了“_é?????_完整三角和的估计”这一历史难题,得到了最佳误差阶估计;对_G.H.??????_与J.E.李特尔伍德关于_??????é??é??_及E.赖特关于塔里问题的结果作了重大的改进,三角和研究成果被国际数学界称为“_????°???????_“。
在代数方面,证明了历史长久遗留的一维射影几何的基本定理;给出了“体的正规子体一定包含在它的中心之中”这个结果的一个简单而直接的证明,被称为“嘉当-布饶尔-华定理”。
与王元教授合作在近代数论方法应用研究方面获重要成果,被称为“华-王方法”。
在代数方面,证明了历史长久遗留的一维射影几何的基本定理;给出了体的正规子体一定包含在它的中心之中这个结果的一个简单而直接的证明,被称为嘉当-布饶尔-华定理。
与王元教授合作在近代数论方法应用研究方面获重要成果,被称为“华-王方法”。
如图的九个方格内已填入一个数,请在其余的八个空格内填上其他的数,使得九个方格内是九个连续自然数,并且横行、竖行及对角线上的三个数的和都相等。那么,所填入八个数之和是多少?
? 10 ?
? ?
【解析】根据题意,10应该是横行、竖行及对角线上每三个数的平均数,所以横行、竖行及对角线上三个数的和是10×3=30,所以三行九个数的和是30×3=90,所以填入的八个数的和即可求出。
解答:30×3-10=80。
?
?
? ?
把1~9这九个数字填写在右图正方形的九个方格中,使得每一横行、每一竖列和每条对角线上的三个数之和都相等。
【解析】方法一:我们首先要弄清每行、每列以及每条对角线上三个数字之和是几。我们可以这样去想:因为1~9这九个数字之和是45,正好是三个横行数字之和,所以每一横行的数字之和等于45÷3=15。也就是说,每一横行、每一竖列以及每条对角线上三个数字之和都等于15。在1~9这九个数字中,三个不同的数相加等于15的有:9+5+1,9+4+2,8+6+1,8+5+2,8+4+3,7+6+2,7+5+3,6+5+4。因此每行、每列以及每条对角线上的三个数字可以是其中任一个算式中的三个数字。因为中心方格中的数既在一个横行中,又在一个竖列中,还在两对角线上,所以它应同时出现在上述的四个算式中,只有5符合条件,因此应将5填在中心方格中。同理,四个角上的数既在一个横行中,又在一个竖列中,还在一条对角线上,所以它应同时出现在上述的三个算式中,符合条件的有2,4,6,8,因此应将2,4,6,8填在四个角的方格中,同时应保证对角线两数的和相等。
方法二:九数斜排,四维突出,上下对调,左右对调。
解答:
一个三阶幻方,每行、每列以及每条对角线上的三个数的和都等于300,幻方中心数是多少?为什么?
【解析】两条对角线及第二行相加,和为100×3=300,其中中心数计算了3次,其它数各算1次,因此这和也等于第一、第三列相加,再加上中心数的三倍。
解答:中心数=(300×3-300×3)÷3=100。一般地,幻和等于中心数的3倍。
在图中的每个空格内填入一个自然数,使得每一横行、每一竖列和每条对角线上的三个数之和都相等。这时右下角方格内的数与8,10有什么关系?
3 10
8
?
? ?
【解析】从左上到右下的对角线与第三行相加,和与第一、第二列相加的和相等,因此,右下角数的2倍等于8+10=18,右下角应填9。
解答:中心数等于(3+9)÷2=6。右下角数的2倍等于8+10=18。
如图,只能用图中已有的3个数填满其余的空格,并要求每个数字必须再使用2次,而且每行、每列及每条对角线上的3个数之和都相等。_???è??é?????_(1.31_KB)_
_???è??é?????_(1.74_KB)_
3 7
? 5 ?
? ?
' W& M; ~/ t( |
【解析】解答:
3 7 5
7 5 3
5 3 7
如图,在一个小方格里最多放入一个p,要想使得同一行、同一列或对角连线上的三个小方格最多不出现三个p,那么在这九个小方格里最多能放入多少个p?
?
?
? ?
p p
p
p
p p
【解析】因为每行每列不能出现3个p,且使九小方格里的p最多,所以每行每列都有2个p,只要保证正方形的对角线上的p不出现3个即可解答问题。
解答:如图2+2+2=6(个),九小方格里最多能放6个p。
如图,方格中横向、纵向和对角线方向的数字和都相等。那么填入4个角上的数字之和是多少?
4
? 4 ?
3
【解析】填入4个角上的数字之和是16。
解答:
3 5 4
5 4 3
4 3 5
如图:只能用图中已有的三个数字填满其中的空格,并要求每个数字必须使用3次,而且每行、每列及每条对角线上的三个数字之和都必须相等。
? ? 8
? 6 ?
4 ? ?
【解析】
6 4 8
8 6 4
4 8 6
解答:
把5~13九个数字填写在下图正方形的九个方格中,使得每一横行、每一竖列和每条对角线上的三个数之和都相等。
? ?
?
?
? ?
【解析】解答:
12 5 10
7 9 11
8 13 6
如图,老师将9个数写在一个九宫格里,让同学们选数,每个同学可以从中选出5个数来求和,小明选的5个数的和是120,小文选的5个数的和是111,如果他们选的数只有一个是一样的,那么这个数是多少?
11 12 13
21 22 23
31 32 33
【解析】因为两个人选的数只有一个是一样的,那么这两个人把表中的这9个数全部选到了,因此这个一样的数就是120+111-(11+12+13+21+22+23+31+32+32),解决问题。
120+111-(11+12+13+21+22+23+31+32+32)=231-198=33
解答:这个数是33。
华罗庚的故事
世界著名_??°??????_,_???????§????é??_院士,_?????????????§????é??_外籍院士,_?????????????§????é??é?????_,联邦德国巴伐利亚科学院院士。中国第一至_???????±???¨???????¤§????§????_委员。
他是中国_è§??????°è??_、矩阵几何学、_????????¤_、_è??????????°è??_与多元复变函数论等多方面研究的创始人和_??????è??_,也是中国在世界上最有_??±??????_的数学家之一,被列为_è?????????§????????????????é??_中当今世界88位数学_??????_之一。国际上以华氏命名的数学科研成果有“_????°???????_”、“华氏不等式”、“华—王方法”等。
在国际上以华氏命名的数学科研成果就有“华氏定理”、“怀依—华不等式”、“华氏不等式”、“普劳威尔—加当华定理”、“华氏算子”、“华—王方法”等。?
20世纪40年代,解决了“_é?????_完整三角和的估计”这一历史难题,得到了最佳误差阶估计;对_G.H.??????_与J.E.李特尔伍德关于_??????é??é??_及E.赖特关于塔里问题的结果作了重大的改进,三角和研究成果被国际数学界称为“_????°???????_“。
在代数方面,证明了历史长久遗留的一维射影几何的基本定理;给出了“体的正规子体一定包含在它的中心之中”这个结果的一个简单而直接的证明,被称为“嘉当-布饶尔-华定理”。
与王元教授合作在近代数论方法应用研究方面获重要成果,被称为“华-王方法”。
在代数方面,证明了历史长久遗留的一维射影几何的基本定理;给出了体的正规子体一定包含在它的中心之中这个结果的一个简单而直接的证明,被称为嘉当-布饶尔-华定理。
与王元教授合作在近代数论方法应用研究方面获重要成果,被称为“华-王方法”。
同课章节目录
