六年级上册数学讲义-小升初培优:第04讲 图形面积认识 (解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义-小升初培优:第04讲 图形面积认识 (解析版)全国通用 |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 08:12:27 | ||
图片预览


文档简介
第四讲 图形面积认识
一个长方形的长增加3米,长方形的面积就增加了12平方米。如果宽减少2米,长方形的面积就减少14平方米。问原来的长方形面积是多少平方米?
【解析】由题意可得,长增加3米,面积增加12平方米,那么可求出原来的宽是12÷3=4米;宽减少2米,面积减少14平方米,那么可求出原来的长是14÷2=7米。
解答:原来的长方形面积是(14÷2)×(12÷3)=28(平方米)。
一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米。求原正方形的面积。
【解析】120-6×6=84 (平方厘米);84÷2=42 (平方厘米);42÷6=7 (厘米);
原来的面积:7×7=49 (平方厘米)。
解答:原正方形的面积为49平方厘米。
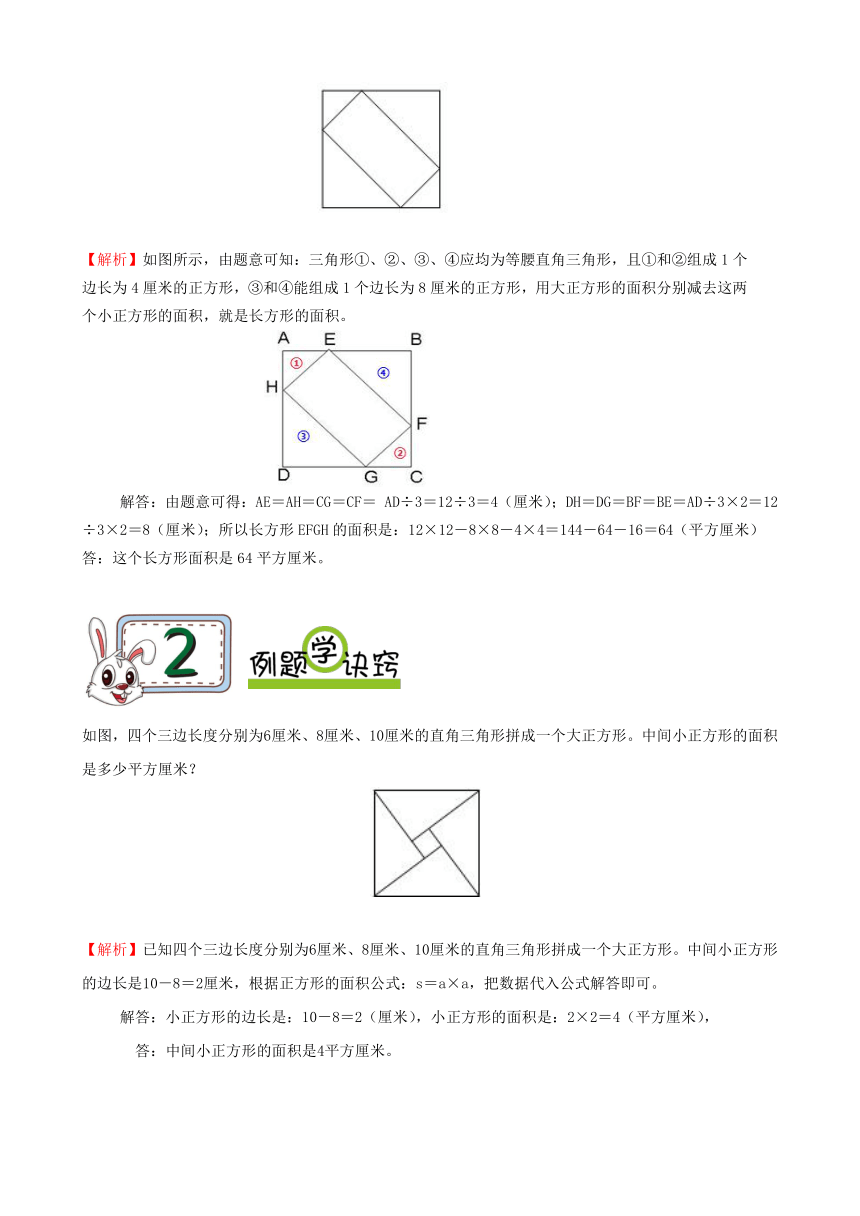
如图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点恰好分别把正方形每条边分成两份,其中长的长度是短的长度2倍,这个长方形面积是多少厘米?
【解析】如图所示,由题意可知:三角形①、②、③、④应均为等腰直角三角形,且①和②组成1个边长为4厘米的正方形,③和④能组成1个边长为8厘米的正方形,用大正方形的面积分别减去这两个小正方形的面积,就是长方形的面积。
解答:由题意可得:AE=AH=CG=CF= AD÷3=12÷3=4(厘米);DH=DG=BF=BE=AD÷3×2=12÷3×2=8(厘米);所以长方形EFGH的面积是:12×12-8×8-4×4=144-64-16=64(平方厘米)
答:这个长方形面积是64平方厘米。
如图,四个三边长度分别为6厘米、8厘米、10厘米的直角三角形拼成一个大正方形。中间小正方形的面积是多少平方厘米?
【解析】已知四个三边长度分别为6厘米、8厘米、10厘米的直角三角形拼成一个大正方形。中间小正方形的边长是10-8=2厘米,根据正方形的面积公式:s=a×a,把数据代入公式解答即可。
解答:小正方形的边长是:10-8=2(厘米),小正方形的面积是:2×2=4(平方厘米),
答:中间小正方形的面积是4平方厘米。
同样大小的长方形小纸片摆成如图的图形。已知小纸片的宽是12厘米,求阴影部分的总面积。
【解析】结合第一排与第二排可以发现,五个小纸片的长等于三个小纸片的长加三个小纸片的宽,这说明,二个小纸片的长等于三个小纸片的宽,于是可以求出小纸片的长。阴影部分是三个正方形,边长正好是小纸片的长与宽的差,即18-12=6厘米,再利用正方形的面积公式即可解决。
解答:小纸片的长是:12×3÷2=18(厘米),所以阴影部分中每个小正方形的边长是:18-12=6(厘米),因此,阴影部分的面积是:6×6×3=108(平方厘米);
答:阴影部分的总面积是108平方厘米。
有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?
【解析】根据题意,可以用下图表示增减变化的情况,从图中可以看出,原来长方形的长为(2720+680)÷(60-50)=340 (米),宽为680÷340+50=52 (米)。
在边长为10的正方形ABCD内,有一个四边形EFGH,FI=2,GJ=1,试求四边形EFGH的面积。
【解析】从图中我们可以看到,去掉了长方形KLMN可以得到四个长方形,分别是
长方形AENH,长方形EBFK,长方形LFCG,长方形HMGD,而所求图形的面积正好是
正方形ABCD面积减去这四个长方形面积的一半,那么如果正方形先加上长方形KLMN
的面积,就得到四边形EFGH面积的2倍,这样就求出四边形EFGH的面积。
解答:(10×10+1×2)÷2=51。
如图,一张长方形纸片,长7厘米,宽5厘米。把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?
【解析】阴影部分的宽是7-5=2 (厘米),长是5-2=3 (厘米),面积是2×3=6 (平方厘米)。
解答:未盖住的阴影部分的面积是6平方厘米。
一块长方形铁板,长15分米,宽l2分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?
【解析】如图,铁板面积比原来减少多少平方分米,就是求阴影部分的面积,用原长方形的面积减去空白部分的面积。15×12-(15-2)×(12-2)=50(平方分米)。
解答:面积比原来减少50平方分米。
四个正方形A、B、C、D如图放置,其中正方形A的周长是24厘米,正方形D的周长是120厘米,则阴影部分的面积会是多少平方厘米?
【解析】由正方形A的周长是24厘米,可知A的边长是6厘米,又由图中能观察出C边长-B边长=A边长=6厘米;由正方形D的周长是120厘米,可知D的边长是30厘米,又由图中能观察出C边长+B边长=D边长=30厘米;由和差公式可得C边长=(30+6)÷2=18厘米,B边长=18-6=12厘米。再由三角形的面积公式即能求得阴影部分的面积。
解答:(120÷4+24÷4)÷2=18 18-6=12
18×18÷2+12×12÷2=234
答:阴影部分的面积会是234平方厘米。
华罗庚的故事-爱国情深
1948年,美国伊利诺大学把华罗庚聘为终身教授,并给了他相当优厚的待遇,希望他把那里建成世界级的代数研究中心。
那一年,华罗庚把夫人和孩子们也接到美国团聚,潦倒奔波了半生,这是他第一次过上恬静的生活。
然而对于漂泊海外报国无门的游子来说,国外恬静安逸的生活无法抚慰内心时常涌动的报国之情。
1949年10月2日,华罗庚听到了一个振奋人心的大好消息,中华人民共和国于10月1日宣告成立了!华罗庚手捧报纸,欣喜若狂,一遍遍地读着新中国建国大典的消息。新中国的成立使他振奋,他渴望着及早回到祖国的怀抱。华罗庚决定回国的消息,使在美的中国人惊讶,更让美国方面难于理解。美国数学界深刻认识到华罗庚的价值,他们不愿意放华罗庚走,提出了十分优厚的条件,试图挽留华罗庚。诸如可以加入美国国籍,增加薪金,建立先进的研究所。伊利诺大学甚至不惜重金,聘请华罗庚为终身教授。华罗庚丝毫不为所动,他的一颗心早已飞向了大洋彼岸的祖国。于是,1950年2月,他悄然离开了生活4年的西半球,乘上一条不大的邮轮,举家回国。
归国途中,华罗庚在香港写了一封《致中国全体留美学生的公开信》。
一个长方形的长增加3米,长方形的面积就增加了12平方米。如果宽减少2米,长方形的面积就减少14平方米。问原来的长方形面积是多少平方米?
【解析】由题意可得,长增加3米,面积增加12平方米,那么可求出原来的宽是12÷3=4米;宽减少2米,面积减少14平方米,那么可求出原来的长是14÷2=7米。
解答:原来的长方形面积是(14÷2)×(12÷3)=28(平方米)。
一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米。求原正方形的面积。
【解析】120-6×6=84 (平方厘米);84÷2=42 (平方厘米);42÷6=7 (厘米);
原来的面积:7×7=49 (平方厘米)。
解答:原正方形的面积为49平方厘米。
如图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点恰好分别把正方形每条边分成两份,其中长的长度是短的长度2倍,这个长方形面积是多少厘米?
【解析】如图所示,由题意可知:三角形①、②、③、④应均为等腰直角三角形,且①和②组成1个边长为4厘米的正方形,③和④能组成1个边长为8厘米的正方形,用大正方形的面积分别减去这两个小正方形的面积,就是长方形的面积。
解答:由题意可得:AE=AH=CG=CF= AD÷3=12÷3=4(厘米);DH=DG=BF=BE=AD÷3×2=12÷3×2=8(厘米);所以长方形EFGH的面积是:12×12-8×8-4×4=144-64-16=64(平方厘米)
答:这个长方形面积是64平方厘米。
如图,四个三边长度分别为6厘米、8厘米、10厘米的直角三角形拼成一个大正方形。中间小正方形的面积是多少平方厘米?
【解析】已知四个三边长度分别为6厘米、8厘米、10厘米的直角三角形拼成一个大正方形。中间小正方形的边长是10-8=2厘米,根据正方形的面积公式:s=a×a,把数据代入公式解答即可。
解答:小正方形的边长是:10-8=2(厘米),小正方形的面积是:2×2=4(平方厘米),
答:中间小正方形的面积是4平方厘米。
同样大小的长方形小纸片摆成如图的图形。已知小纸片的宽是12厘米,求阴影部分的总面积。
【解析】结合第一排与第二排可以发现,五个小纸片的长等于三个小纸片的长加三个小纸片的宽,这说明,二个小纸片的长等于三个小纸片的宽,于是可以求出小纸片的长。阴影部分是三个正方形,边长正好是小纸片的长与宽的差,即18-12=6厘米,再利用正方形的面积公式即可解决。
解答:小纸片的长是:12×3÷2=18(厘米),所以阴影部分中每个小正方形的边长是:18-12=6(厘米),因此,阴影部分的面积是:6×6×3=108(平方厘米);
答:阴影部分的总面积是108平方厘米。
有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?
【解析】根据题意,可以用下图表示增减变化的情况,从图中可以看出,原来长方形的长为(2720+680)÷(60-50)=340 (米),宽为680÷340+50=52 (米)。
在边长为10的正方形ABCD内,有一个四边形EFGH,FI=2,GJ=1,试求四边形EFGH的面积。
【解析】从图中我们可以看到,去掉了长方形KLMN可以得到四个长方形,分别是
长方形AENH,长方形EBFK,长方形LFCG,长方形HMGD,而所求图形的面积正好是
正方形ABCD面积减去这四个长方形面积的一半,那么如果正方形先加上长方形KLMN
的面积,就得到四边形EFGH面积的2倍,这样就求出四边形EFGH的面积。
解答:(10×10+1×2)÷2=51。
如图,一张长方形纸片,长7厘米,宽5厘米。把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?
【解析】阴影部分的宽是7-5=2 (厘米),长是5-2=3 (厘米),面积是2×3=6 (平方厘米)。
解答:未盖住的阴影部分的面积是6平方厘米。
一块长方形铁板,长15分米,宽l2分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?
【解析】如图,铁板面积比原来减少多少平方分米,就是求阴影部分的面积,用原长方形的面积减去空白部分的面积。15×12-(15-2)×(12-2)=50(平方分米)。
解答:面积比原来减少50平方分米。
四个正方形A、B、C、D如图放置,其中正方形A的周长是24厘米,正方形D的周长是120厘米,则阴影部分的面积会是多少平方厘米?
【解析】由正方形A的周长是24厘米,可知A的边长是6厘米,又由图中能观察出C边长-B边长=A边长=6厘米;由正方形D的周长是120厘米,可知D的边长是30厘米,又由图中能观察出C边长+B边长=D边长=30厘米;由和差公式可得C边长=(30+6)÷2=18厘米,B边长=18-6=12厘米。再由三角形的面积公式即能求得阴影部分的面积。
解答:(120÷4+24÷4)÷2=18 18-6=12
18×18÷2+12×12÷2=234
答:阴影部分的面积会是234平方厘米。
华罗庚的故事-爱国情深
1948年,美国伊利诺大学把华罗庚聘为终身教授,并给了他相当优厚的待遇,希望他把那里建成世界级的代数研究中心。
那一年,华罗庚把夫人和孩子们也接到美国团聚,潦倒奔波了半生,这是他第一次过上恬静的生活。
然而对于漂泊海外报国无门的游子来说,国外恬静安逸的生活无法抚慰内心时常涌动的报国之情。
1949年10月2日,华罗庚听到了一个振奋人心的大好消息,中华人民共和国于10月1日宣告成立了!华罗庚手捧报纸,欣喜若狂,一遍遍地读着新中国建国大典的消息。新中国的成立使他振奋,他渴望着及早回到祖国的怀抱。华罗庚决定回国的消息,使在美的中国人惊讶,更让美国方面难于理解。美国数学界深刻认识到华罗庚的价值,他们不愿意放华罗庚走,提出了十分优厚的条件,试图挽留华罗庚。诸如可以加入美国国籍,增加薪金,建立先进的研究所。伊利诺大学甚至不惜重金,聘请华罗庚为终身教授。华罗庚丝毫不为所动,他的一颗心早已飞向了大洋彼岸的祖国。于是,1950年2月,他悄然离开了生活4年的西半球,乘上一条不大的邮轮,举家回国。
归国途中,华罗庚在香港写了一封《致中国全体留美学生的公开信》。
同课章节目录
